Quadratic equations are one of the most important topics in Class 10 Mathematics. They form the foundation for higher-level algebra and are widely used in real-life problem-solving, from calculating areas to predicting profits. In this lesson, we will explore the key concepts of quadratic equations, step-by-step methods to solve them, and clear examples to make your understanding strong and exam-ready.

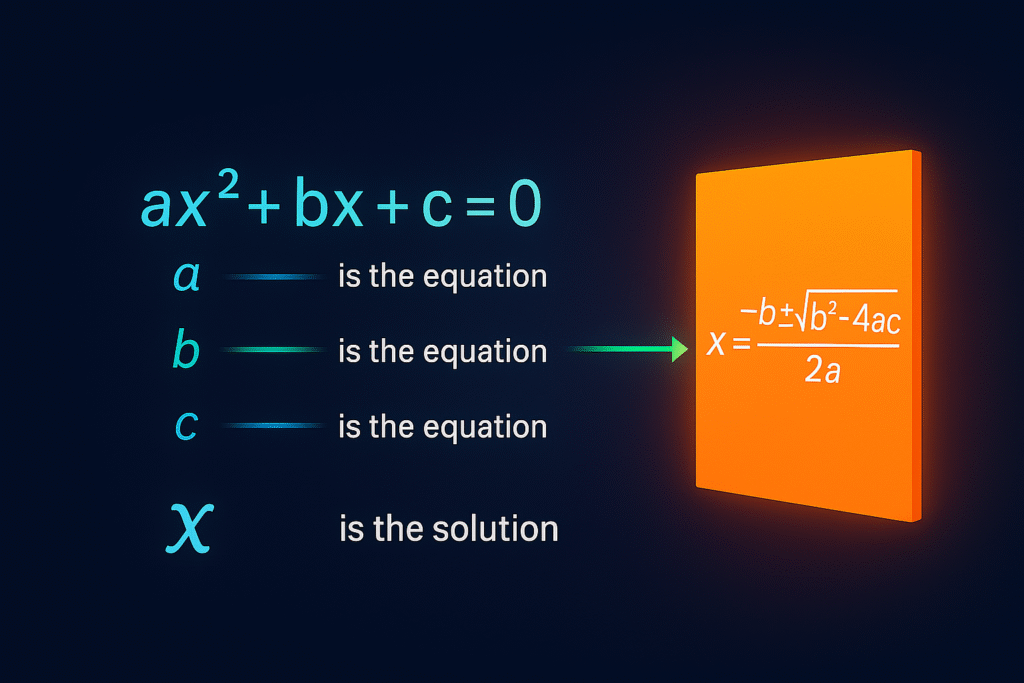
Quadratic Equations Concepts with Examples – Class 10 Math

Quadratic Equations 🚀

Concepts with Examples for Class 10 Math

A visual representation of a quadratic equation

What is a Quadratic Equation?

A quadratic equation is a polynomial equation of the second degree. In simpler terms, it’s an equation where the highest power of the variable (usually x) is 2. Think of it as a special kind of problem that has up to two solutions!

The Standard Form

The standard form of a quadratic equation is:

ax² + bx + c = 0

Where ‘a’, ‘b’, and ‘c’ are real numbers, and **a ≠ 0**.

a is the coefficient of the x² term.
b is the coefficient of the x term.
c is the constant term.

Methods of Solving Quadratic Equations

Method 1: Factoring

This method involves breaking down the middle term (bx) into two parts whose sum is b and whose product is a · c.

Example: Solve x² + 5x + 6 = 0

Step 1: Find two numbers that add up to 5 and multiply to 6. The numbers are 2 and 3.
Step 2: Split the middle term: x² + 2x + 3x + 6 = 0
Step 3: Factor by grouping: x(x+2) + 3(x+2) = 0
Step 4: Factor out the common term: (x+2)(x+3) = 0
Step 5: Set each factor to zero to find the roots:
x + 2 = 0 ⟹ x = -2
x + 3 = 0 ⟹ x = -3

Method 2: Quadratic Formula

This formula is a universal way to find the roots of any quadratic equation, regardless of whether it can be factored or not.

x = [-b ± sqrt(b² – 4ac)] / 2a

Example: Solve 2x² + 4x – 6 = 0

Step 1: Identify a, b, and c. Here, a=2, b=4, and c=-6.
Step 2: Substitute the values into the formula:
x = [-4 ± sqrt(4² – 4(2)(-6))] / 2(2)
x = [-4 ± sqrt(16 + 48)] / 4 = [-4 ± sqrt(64)] / 4
x = (-4 ± 8) / 4
Step 3: Find the two roots:
x₁ = (-4 + 8) / 4 = 4 / 4 = 1
x₂ = (-4 – 8) / 4 = -12 / 4 = -3

Method 3: Completing the Square

This method converts the equation into a perfect square trinomial. It’s especially useful when the equation cannot be easily factored.

Example: Solve x² + 6x – 7 = 0

Step 1: Move the constant term to the other side: x² + 6x = 7
Step 2: Add (b/2)² to both sides. Here b=6, so (6/2)² = 3² = 9.
x² + 6x + 9 = 7 + 9
Step 3: Factor the left side and simplify the right side:
(x+3)² = 16
Step 4: Take the square root of both sides:
x + 3 = ± sqrt(16)
x + 3 = ± 4
Step 5: Solve for x:
x = -3 + 4 = 1
x = -3 – 4 = -7

Nature of Roots: The Discriminant

The **discriminant**, denoted by the Greek letter delta (Δ), is the expression inside the square root in the quadratic formula: Δ = b² – 4ac. It tells you about the nature of the roots without actually solving the equation.

Case 1: If Δ > 0

The roots are **real and distinct** (two different real numbers).

Case 2: If Δ = 0

The roots are **real and equal** (one real number repeated twice).

Case 3: If Δ < 0

There are **no real roots** (the roots are imaginary numbers, which you will learn about in higher classes).

Quadratic Equations Concepts with Examples are one of the most fundamental concepts in algebra and are widely used in real-life applications like physics, engineering, business, and economics.

Tip: If you’re preparing for board exams, we recommend this best-selling Class 10 Mathematics Question Bank that includes solved quadratic equation problems, mind maps, and MCQs.

This guide is based on the latest CBSE syllabus and NCERT guidelines and is perfect for quick revision, doubt-clearing, or preparing for school tests and board exams.

Quadratic Equations Concepts with Examples

Quadratic Equations Concepts with Examples are one of the most fundamental concepts in algebra and are widely used in real-life applications like physics, engineering, business, and economics. In this post, we will explore the concept of quadratic equations, methods to solve them, graphical understanding, and important examples to help Class 10 students understand the chapter deeply.

Tip: If you’re preparing for board exams, we recommend this best-selling Class 10 Mathematics Question Bank that includes solved quadratic equation problems, mind maps, and MCQs.

What is a Quadratic Equation? A quadratic equation is a second-degree polynomial equation in a single variable x, with the general form:

ax² + bx + c = 0

Where:

a, b, and c are real numbers
a ≠ 0 (If a = 0, it becomes a linear equation)

Examples:

x² + 5x + 6 = 0
2x² – 3x – 5 = 0

Key Terms in Quadratic Equations

Coefficient of x² (a): Determines the direction and shape of the parabola.
Coefficient of x (b): Affects the position of the vertex and axis of symmetry.
Constant term (c): Determines the y-intercept.
Discriminant (D): b² – 4ac, determines the nature of the roots.
Roots/Zeros of a Quadratic Equation: The values of x that satisfy the equation.

Methods of Solving Quadratic Equations

Factorization Method

Used when the quadratic equation can be expressed as a product of two linear factors.

Example:
x² – 7x + 12 = 0
(x – 3)(x – 4) = 0
x = 3, 4

Completing the Square Method

Convert the equation into a perfect square.

Example:
x² + 6x + 5 = 0
x² + 6x = -5
x² + 6x + 9 = 4 (add 9 both sides)
(x + 3)² = 4
x = -3 ± 2
x = -1, -5

Quadratic Formula

Use the standard formula:

x = (-b ± √(b² – 4ac)) / 2a

Example:
2x² – 3x – 2 = 0
a = 2, b = -3, c = -2
x = (3 ± √(9 + 16)) / 4
x = (3 ± √25) / 4
x = (3 ± 5) / 4
x = 2, -1/2

Tip: Use a scientific calculator for solving quadratic equations easily.

Graphical Method

Plot the graph of the equation. The x-intercepts (where the graph cuts the x-axis) are the roots.

If the parabola cuts the x-axis at two points → two real roots.
If it touches the x-axis at one point → one real root.
If it doesn’t cut the x-axis → no real root (imaginary).

Nature of Roots Using Discriminant

D = b² – 4ac

Value of D	Nature of Roots
D > 0	Two distinct real roots
D = 0	Two equal real roots
D < 0	No real roots (Imaginary)

Examples:

x² – 5x + 6 = 0 → D = 1 → Real and distinct roots
x² – 6x + 9 = 0 → D = 0 → Real and equal roots
x² + x + 1 = 0 → D = -3 → Imaginary roots

Graphical Understanding of Quadratic Equations

If a > 0 → Parabola opens upward
If a < 0 → Parabola opens downward
Vertex of the parabola is at x = -b / 2a
Y-intercept is the value of c

Example:

Equation: y = x² – 4x + 3
Vertex: x = 2
Roots: x = 1, 3
Graph opens upward (a = 1)

You can use free graphing tools like Desmos or GeoGebra to plot quadratic curves.

Important Examples of Quadratic Equations Concepts with Examples

Example 1:
Solve x² – 6x + 8 = 0
(x – 2)(x – 4) = 0
x = 2, 4

Example 2:
Solve 3x² + 2x – 1 = 0
x = (-2 ± √(4 + 12)) / 6
x = (-2 ± √16) / 6
x = (-2 ± 4) / 6
x = 1/3, -1

Example 3:
Find the nature of roots of x² + 4x + 5 = 0
D = 16 – 20 = -4
No real roots (imaginary)

Applications of Quadratic Equations Concepts with Examples

Quadratic equations are used in:

Physics (projectile motion)
Business (profit calculation)
Engineering (design problems)
Geometry (area of figures)
Economics (maximum profit or minimum cost)

Class 10 Board Exam Questions on Quadratic Equations

Q1. Solve: x² + 7x + 10 = 0
(x + 2)(x + 5) = 0 → x = -2, -5

Q2. Solve: x² – 2x – 8 = 0 using formula
x = (2 ± √(4 + 32)) / 2 = (2 ± √36)/2 = (2 ± 6)/2 → x = 4, -2

Practice Questions

Solve x² + 3x – 10 = 0
Find the roots of 5x² + 6x + 1 = 0
What is the nature of roots of 2x² – 4x + 2 = 0?
Using completing the square, solve x² – 8x + 15 = 0

Answers:

x = 2, -5
x = -1/5, -1
D = 0 → equal roots
x = 3, 5

Useful Books and Tools for Practice

Class 10 Math Question Bank (2025 edition)
Algebra Made Easy Workbook
Scientific Calculator
Quadratic Equation Solving App
Graphing Calculator App (GeoGebra)

Conclusion

Understanding quadratic equations is essential for scoring well in Quadratic Equations Concepts with Examples and for building a strong base in algebra. Whether you solve by factorization, completing the square, or using the quadratic formula, regular practice is key. Always analyze the nature of the roots and try plotting the graphs to understand the visual representation of equations.

1. From This Section:

In Quadratic Equations Concepts with Examples is a crucial chapter that builds on algebraic foundations.”

In Class 10 Maths Quadratic Equations chapter, students strengthen their algebraic foundations.”

2. From This Section:

Let’s take a look at the standard form of a quadratic equation.”

3. From This Section:

Students often get confused between linear equations and quadratic equations.”

4. From the ‘Practice Questions’ section:

Here are some Class 10 Maths sample questions based on real-world applications.”

🔗 Official NCERT Textbook PDF for Quadratic Equations Concepts with Examples:

NCERT Resources (for Class 10):

Access Ncert Text Book

NEET BIOLOGY ECOSYSTEM

📘 Math & Science Solutions by Class

🔹 Class 10

🔹 Class 9

🔹 Class 8

🔹 Class 7

🔹 Class 6

🔹 Class 11

Learn more about circle formulas from NCERT.

Class-wise Solutions

Class 12:

Class 12 Physics – NCERT Solutions

Class 12 Chemistry – NCERT Solutions

Class 11:

Class 10:

Class 9:

Class 8:

Class 7:

Class 7 Science – Oxford Solutions

Class 6:

Class 6 Science – Oxford Solutions

Subject-wise Solutions

Physics:

Chemistry:

Biology:

Class 11 Biology – NCERT Solutions

Math:

Science:

NEET BIOLOGY

2 Comments

Forex Maroc says:
July 26, 2025 at 12:11 pm
Excellent web site you have here.. It’s difficult to
find good quality writing like yours nowadays.
I seriously appreciate people like you! Take care!!
1. Sudip says:
  July 26, 2025 at 4:34 pm
  Thank you so much for encouraging

Quadratic Equations Concepts with Examples – Class 10 Math

Quadratic Equations 🚀

What is a Quadratic Equation?

The Standard Form