Ex 1.3
Ch 2 polynomials

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2

Question 1.
Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution: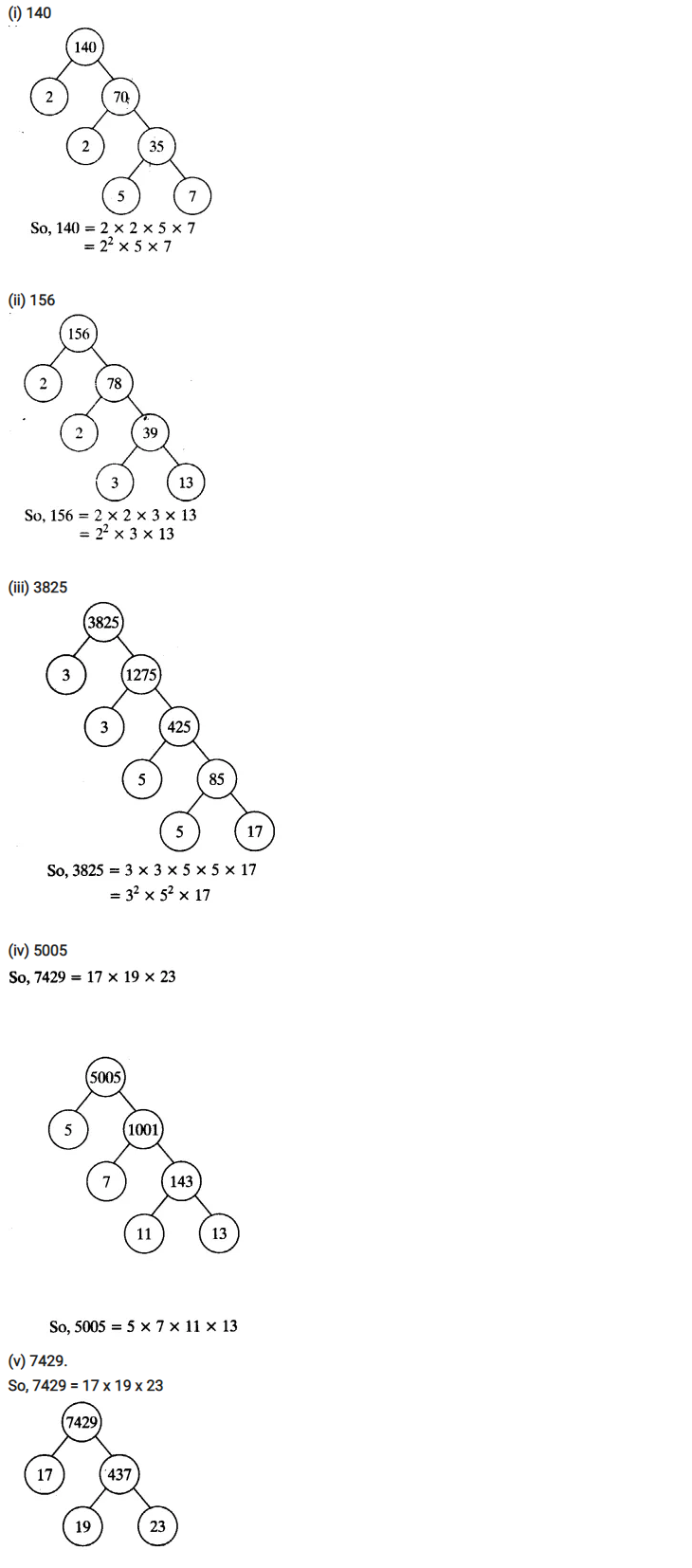
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Q15

Ex 1.2 Class 10 Maths Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM x HCF = Product of the two numbers:
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
chapter 1 class 10 maths Ex 1.2 Q2

Ex 1.2 Class 10 Maths Question 3.
Find the LCM and HCF of the following integers by applying the prime factorization method:
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solution:
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Q3
Ex 1.2 Class 10 Maths Question 4:
Given that HCF (306, 657) = 9, find LCM (306, 657).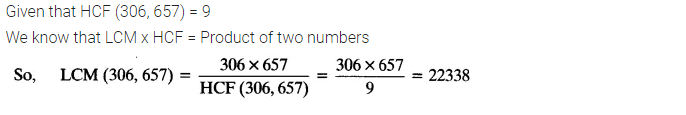
Real Numbers Class 10 Maths Chapter 1 NCERT Solutions Ex 1.2 Q4
Ex 1.2 Class 10 Maths Question 5.
Check whether 6n can end with the digit 0 for any natural number n.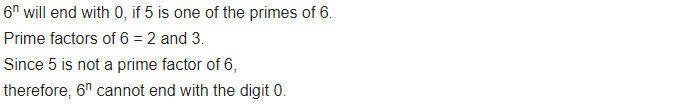
Real Numbers Class 10 Maths Chapter 1 NCERT Solutions Ex 1.2 Q5
Ex 1.2 Class 10 Maths Question 6.
Explain why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are composite numbers.
Chapter 1 Class 10 Maths Real Numbers NCERT Solutions Ex 1.2 Q6
Ex 1.2 Class 10 Maths Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:
Chapter 1 Class 10 Maths Real Numbers NCERT Solutions Ex 1.2 Q7

NCERT Solutions for Class 10 Maths Chapter 1 – Real Numbers (Ex 1.2)

Introduction to Exercise 1.2 – Real Numbers

Exercise 1.2 of NCERT Class 10 Maths Chapter 1 – Real Numbers focuses on the Fundamental Theorem of Arithmetic, which states that every composite number can be uniquely expressed as a product of prime numbers (except for the order of the factors). This concept is crucial for solving problems related to factorization and the highest common factor (HCF) and lowest common multiple (LCM) of numbers.

In this section, we will cover:

  • Prime factorization method
  • Finding HCF and LCM using prime factorization
  • Relationship between HCF and LCM

Let’s go through NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2 step by step.

NCERT Solutions for Class 10 Maths Chapter 1 – Real Numbers (Ex 1.2) Questions & Answers

Question 1:

Find the LCM and HCF of 26 and 91 and verify that HCF × LCM = Product of the numbers.

Solution:

Step 1: Find the Prime Factorization

  • 26=2×1326 = 2 \times 1326=2×13
  • 91=7×1391 = 7 \times 1391=7×13

Step 2: Calculate HCF

  • Common factor = 13
  • So, HCF (26, 91) = 13

Step 3: Calculate LCM

  • LCM = 2×7×13=1822 \times 7 \times 13 = 1822×7×13=182
  • So, LCM (26, 91) = 182

Step 4: Verify HCF × LCM = Product of the Numbers

  • HCF × LCM = 13 × 182 = 2366
  • Product of numbers = 26 × 91 = 2366
  • Since both values are equal, the verification is correct ✅.

Question 2:

Find the HCF and LCM of 510 and 92 using the prime factorization method.

Solution:

Step 1: Prime Factorization

  • 510=2×3×5×17510 = 2 \times 3 \times 5 \times 17510=2×3×5×17
  • 92=2×2×2392 = 2 \times 2 \times 2392=2×2×23

Step 2: HCF (Greatest Common Factor)

  • Common factor = 2
  • So, HCF (510, 92) = 2

Step 3: LCM (Least Common Multiple)

  • LCM = 22×3×5×17×232^2 \times 3 \times 5 \times 17 \times 2322×3×5×17×23
  • =23460= 23460=23460
  • So, LCM (510, 92) = 23460

Question 3:

Prove that HCF × LCM = Product of the two numbers for 336 and 54.

Solution:

Step 1: Prime Factorization

  • 336=24×3×7336 = 2^4 \times 3 \times 7336=24×3×7
  • 54=2×3354 = 2 \times 3^354=2×33

Step 2: Calculate HCF

  • Common factors: 212^121 and 313^131
  • So, HCF (336, 54) = 2 × 3 = 6

Step 3: Calculate LCM

  • LCM = 24×33×72^4 \times 3^3 \times 724×33×7
  • =3024= 3024=3024
  • So, LCM (336, 54) = 3024

Step 4: Verification

  • HCF × LCM = 6 × 3024 = 18144
  • Product of numbers = 336 × 54 = 18144
  • Since both values are equal, the verification is correct ✅.
Key Takeaways from NCERT Solutions for Class 10 Maths Chapter 1 (Ex 1.2)

✔ Fundamental Theorem of Arithmetic is used for prime factorization.
✔ HCF is obtained by multiplying the common prime factors with the lowest power.
✔ LCM is obtained by multiplying all the prime factors with the highest power.
✔ The formula HCF × LCM = Product of numbers always holds true

For the official Class 10 Mathematics Solutions, you can visit:

  1. NCERT Textbooks (for Class 10):
    https://ncert.nic.in/textbook.php?class=10