NCERT Solutions for Class 10 Maths Chapter 4 | Quadratic Equations Ex 4.2
Ex 4.2 Class 10 Maths | NCERT Solutions for Class 10 Maths Chapter 4 | Quadratic Equations Ex 4.2
Question 1.
Find the roots of the following quadratic equations by factorisation:
(i) x2 -3x – 10 = 0
(ii) 2x2 + x – 6 = 0
(iii) √2x2 + 7x + 5√2 = 0
(iv) 2x2 – x + [Math Processing Error] = 0 8
(v) 100 x2 – 20 X + 1 = 0
Solution:



Ex 4.2 Class 10 Maths
Question 2.
Solve the following situations mathematically:
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹750. We would like to find out the number of toys produced on that day.
Solution: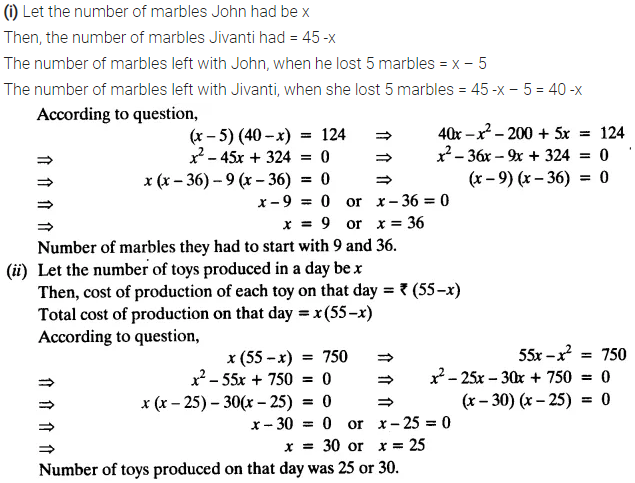
Ex 4.2 Class 10 Maths
Question 3.
Find two numbers whose sum is 27 and product is 182.
Solution: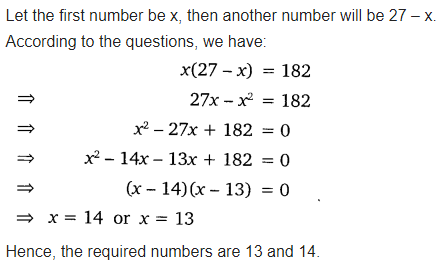
Ex 4.2 Class 10 Maths Question 4.
Find two consecutive positive integers, the sum of whose squares is 365.
Solution: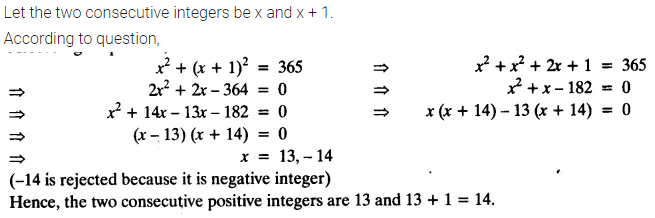
Ex 4.2 Class 10 Maths
Question 5.
The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
NCERT Solutions for Class 10 Maths Chapter 4 | Quadratic Equations Ex 4.2
Ex 4.2 Class 10 Maths
Question 6.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was ₹90, find the number of articles produced and the cost of each article.
Solution:
You can access the official NCERT Solutions for Class 10 Mathematics on the NCERT website at the following link:
NCERT Class 10 Mathematics Solutions
This page will guide you to the textbook and solutions, as provided by the National Council of Educational Research and Training (NCERT).



