Pair Of Linear Equations In Two Variables Ex 3.1 Solution

This exercise introduces the concept of solving real-life problems using linear equations in two variables. Each problem can be translated into a pair of equations, helping us find the values of two unknowns. By accessing the solutions to this exercise, students can:

Learn how to form equations from word problems
Understand how to represent situations algebraically
Visualize equations graphically using straight lines
Identify whether a pair of equations has one solution, no solution, or infinitely many solutions

The solutions are step-by-step, easy to follow, and designed to build a strong foundation for solving linear equations confidently.

Pair of Linear Equations in Two Variables Ex 3.1 – Full Chapter Solutions

Question 1.
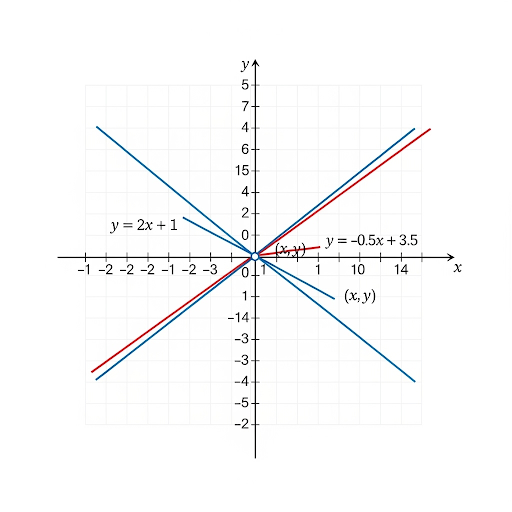
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. Isn’t this interesting? Represent this situation algebraically and graphically.
Solution:

Let:

Aftab’s age = x
Daughter’s age = y

Equations:

Seven years ago:
x − 7 = 7(y − 7)
⇒ x − 7y = -42
Three years from now:
x + 3 = 3(y + 3)
⇒ x − 3y = 6

Solving:

From equations:
x − 7y = -42
x − 3y = 6

Subtract:
(−4y = −48) ⇒ y = 12
Substitute:
x − 3(12) = 6 ⇒ x = 42

Answer:

Aftab = 42 years, Daughter = 12 years

Graphical form:

Equations:

x = 7y − 42
x = 3y + 6

Lines intersect at (42, 12)

Question 2- Pair of Linear Equations in Two Variables Ex 3.1
The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹1300. Represent this situation algebraically and geometrically.
Solution:

Let the cost of 1 bat be x and 1 ball be y.

From the given:

3x + 6y = 3900
x + 3y = 1300

Simplify the first equation:

Divide by 3:
x + 2y = 1300

So the two equations are:
x + 2y = 1300
x + 3y = 1300

To represent geometrically:

From x + 2y = 1300 ⇒ x = 1300 − 2y
From x + 3y = 1300 ⇒ x = 1300 − 3y

Table for x = 1300 − 2y:

y = 100 → x = 1100
y = 200 → x = 900

Table for x = 1300 − 3y:

y = 100 → x = 1000
y = 200 → x = 700

Plot both equations on a graph. The point where the lines intersect gives the solution for x and y.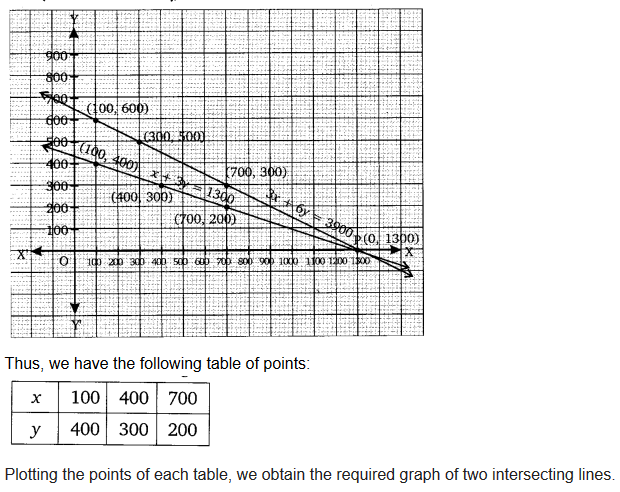
Pair Of Linear Equations In Two Variables Class 10 Maths NCERT Solutions Ex 3.1 Q2.1

Ex 3.1 – Pair of Linear Equations in Two Variables Ex 3.1
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹300. Represent the situation algebraically and geometrically.
Solution:
Let the cost of 1 kg of apples be x and 1 kg of grapes be y.

From the given:

2x + y = 160
4x + 2y = 300

Simplify the second equation:

Divide by 2:
2x + y = 150

Now the two equations are:

2x + y = 160
2x + y = 150

These are two parallel lines with no solution (inconsistent system).

Geometric representation:

From 2x + y = 160 ⇒ y = 160 − 2x
From 2x + y = 150 ⇒ y = 150 − 2x

Table for y = 160 − 2x:
x = 0 → y = 160
x = 50 → y = 60

Table for y = 150 − 2x:
x = 0 → y = 150
x = 50 → y = 50

Plot both lines on the graph. Since the lines are parallel and do not intersect, the system has no solution.

Pair of Linear Equations in Two Variables Ex 3.1 Mind Map

System of a Pair of Linear Equations in Two Variables

An equations of the form Ax + By + C = 0 is called a linear equation in two variables x and y where A, B, C are real numbers.
Two linear equations in the same two variables are called a pair of linear equations in two variables. Standard form of linear equations in two variables.
a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₁ = 0
where a₁, a₂, b₁, b₂, c₁, c₂ are real numbers such that

Representation of Linear Equation In Two Variables

Every linear equation in two variables graphically represents a line and each solution (x, y) of a linear equation in two variables, ax + by + c = 0, corresponds to a point on the line representing the equation, and vice versa.

Ploting Linear Equation in Two Variables on the Graph

There are infinitely many solutions of each linear equation. So, we choose at least any two values of one variable & get the value of other variable by substitution, i.e; Consider; Ax + By + C = 0 We can write the above linear equation as:

Here, we can choose any values of x & can find corresponding values of y.
After getting the values of (x, y) we plot them on the graph thereby getting the line representing Ax + By + C = 0.

Method of Solution of a Pair of Linear Equations in Two Variables

Coordinate of the point (x, y) which satisfy the system of pair of linear equations in two variables is the required solution. This is the point where the two lines representing the two equations intersect each other.
There are two methods of finding solution of a pair of Linear equations in two variables.
(1) Graphical Method : This method is less convenient when point representing the solution has non-integral co-ordinates.
(2) Algebraic Method : This method is more convenient when point representing the solution has non-integral co-ordinates.
This method is further divided into three methods:
(i) Substitution Method,
(ii) Elimination Method and
(iii) Cross Multiplication Method.

Consistency and Nature of the Graphs – Pair of Linear Equations in Two Variables Ex 3.1

Consider the standard form of linear equations in two variables.
a₁x + b₁y + C₁ = 0; a₂x + b₂y + c₂ = 0
While solving the above system of equation following three cases arise.
(i) If a1a2≠b1b2; system is called consistent, having unique solution and pair of straight lines representing the above equations intersect at one point only
(ii) If a1a2=b1b2=c1c2 ; system is called dependent and have infinetly many solution. Pair of lines representing the equations coincide.

Algebraic Method of Solution – Pair of Linear Equations in Two Variables Ex 3.1

Consider the following system of equation
a₁x + b₁y + c₁ =0; a₂x + b₂y + c₁ =0
There are following three methods under Algebraic method to solve the above system.

(i) Substitution method – Pair of Linear Equations in Two Variables Ex 3.1

(a) Find the value of one variable, say y in terms of x or x in terms of y from one equation.
(b) Substitute this value in second equation to get equation in one variable and find solution.
(c) Now substitute the value/solution so obtained in step (b) in the equation got in step (a).

(ii) Elimination Method – Pair of Linear Equations in Two Variables Ex 3.1

(a) If coefficient of any one variable are not same in both the equation multiply both the equation with suitable non-zero constants to make coefficient of any one variable numerically equal.
(b) Add or subtract the equations so obtained to get equation in one variable and solve it.
(c) Now substitute the value of the variable got in the above step in either of the original equation to get value of the other variable.

(iii) Cross multiplication method – Pair of Linear Equations in Two Variables Ex 3.1

For the pair of Linear equations intwo variables:
a₁x + b₁y + C₁ = 0
a₂x + b₂y + c₂ = 0
Consider the following diagram.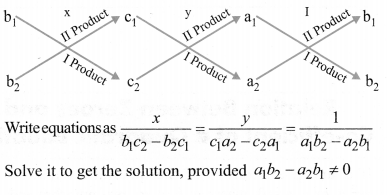
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 4
Solve it to get the solution, provided a₁b₂ – a₂b₁ ≠ 0

Equations Reducible to a Pair of Linear Equations in Two Variables

Sometimes pair of equations are not linear (or not in standard form), then they are altered so that they reduce to a pair of linear equations in standard form.
For example;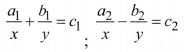
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 5
Here we substitute 1x = p & \frac{1}{y} = q, the above equations reduces to:
a₁p + b₁q = c₁ ; a₂p – b₂q = c₂
Now we can use any method to solve them.