Exercise 13.5 includes comprehensive mixed problems based on all the concepts covered in the chapter—surface areas, volumes, and combinations of solids, including conversion of solids and frustum of a cone.

This exercise is designed to test students’ overall understanding of the chapter through application-based and higher-order thinking questions. Solving these problems helps strengthen concepts, improve calculation accuracy, and enhance problem-solving speed—key skills for scoring well in the board exam.
Class 10 Math Ch Surface Areas and Volumes Ex 13.5
Ex 13.5 Class 10 Maths Question 1.
A copper wire, 3 mm in diameter is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
Solution:
Ex 13.5 Class 10 Maths Question 2.
A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed.
Solution:
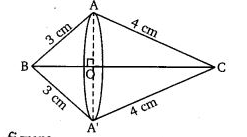
A right triangle has sides 3 cm and 4 cm (other than the hypotenuse). It is revolved about its hypotenuse, forming a double cone. Find the volume and surface area of the double cone.
Step 1: Calculate the hypotenuse using Pythagoras theorem.
Hypotenuse = √(3² + 4²) = √(9 + 16) = √25 = 5 cm.
Step 2: Calculate the radius of the common base (the altitude from the right angle to the hypotenuse).
Area of the triangle = (1/2) × 3 × 4 = 6 cm².
Also, area = (1/2) × hypotenuse × radius.
So, 6 = (1/2) × 5 × radius → radius = 12 / 5 = 2.4 cm.
Step 3: Calculate the volume of the double cone.
Volume = (1/3) × π × radius² × (sum of the legs)
= (1/3) × π × (2.4)² × 5
= (1/3) × π × 5.76 × 5
= (28.8 / 3) × π = 9.6 × π ≈ 30.14 cubic cm.
Step 4: Calculate the surface area of the double cone.
Surface area = π × radius × (sum of the legs)
= π × 2.4 × (3 + 4)
= π × 2.4 × 7 = 16.8 × π ≈ 52.75 square cm.
Ex 13.5 Class 10 Maths Question 3.
A cistern measuring 150 cm x 120 cm x 110 cm has 129600 cm3 water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm x 7.5 cm x 6.5 cm?
Solution:
Step 1: Cistern Volume
Cistern dimensions:
150 cm × 120 cm × 110 cm =
Volume of cistern = 150 × 120 × 110 = 1,980,000 cm³
Step 2: Water already in the cistern
Given: 129,600 cm³
So, remaining volume available =
1,980,000 – 129,600 = 1,850,400 cm³
Step 3: Volume of one brick
Brick dimensions:
22.5 cm × 7.5 cm × 6.5 cm =
Volume = 22.5 × 7.5 × 6.5 = 1096.875 cm³
Step 4: Water absorbed by one brick
Each brick absorbs 1/17 of its own volume:
= 1096.875 ÷ 17 = 64.52 cm³
Now here’s the key point:
Only the volume of the brick minus the water it absorbs is added to the cistern.
Because when we place a brick:
- Its full volume displaces water, contributing to filling the cistern.
- But it absorbs some water too (so part of the existing water disappears into it).
Hence, net volume added per brick =
Volume of brick – water absorbed
= 1096.875 – 64.52 = 1032.35 cm³
Step 5: Number of bricks that can be placed
Number of bricks × 1032.35 ≤ 1,850,400
x ≤ 1,850,400 ÷ 1032.35 ≈ 1792.01
So the maximum number of bricks that can be placed is 1792.
Ex 13.5 Class 10 Maths Question 4.
In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km, show that the total rainfall was approximately equivalent to addition to the normal water of three rivers each 1072 km long. 75 m wide and 3 m deep.
Solution
Rainfall = 10 cm = 0.1 m
Area of valley = 7280 km² = 7280 × (1000 × 1000) = 7,280,000,000 m²
Volume of rainfall = Area × Height of rainfall
= 7,280,000,000 × 0.1 = 728,000,000 m³
Rainfall = 10 cm = 0.1 m
Area of valley = 7280 km² = 7280 × (1000 × 1000) = 7,280,000,000 m³
Now compare it to the volume of water in 3 rivers:
Each river is:
- Length = 1072 km = 1,072,000 m
- Width = 75 m
- Depth = 3 m
Volume of one river = length × width × depth
= 1,072,000 × 75 × 3 = 241,200,000 m³
Volume of 3 such rivers = 3 × 241,200,000 = 723,600,000 m³
Yes, the total rainfall is approximately equal to the water in 3 rivers of the given dimensions.
Ex 13.5 Class 10 Maths Question 5.
An oil funnel made of tin sheer consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel.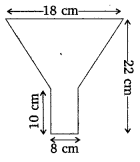
Solution: Dimensions:
- Height of cylindrical portion = 10 cm
- Diameter of cylindrical portion = 8 cm → Radius = 4 cm
- Total height of the funnel = 22 cm
- Height of frustum = 22 – 10 = 12 cm
- Diameter of top of funnel = 18 cm → Radius = 9 cm
- Radius of bottom of frustum (same as top of cylinder) = 4 cm
Curved Surface Area (CSA) of Cylinder:
Formula: 2 × π × radius × height
= 2 × 3.1416 × 4 × 10
= 251.33 cm²
Curved Surface Area of Frustum of a Cone:
Formula: π × (R + r) × slant height
Where:
- R = top radius = 9 cm
- r = bottom radius = 4 cm
- Height of frustum = 12 cm
- Slant height = √[(R – r)² + height²]
= √[(9 – 4)² + 12²] = √(25 + 144) = √169 = 13 cm
Now CSA = 3.1416 × (9 + 4) × 13
= 3.1416 × 13 × 13
= 530.93 cm²
Total Tin Sheet Area = CSA of cylinder + CSA of frustum
= 251.33 + 530.93 = 782.26 cm²
Final Answer:
The area of the tin sheet required is approximately 782.26 cm².
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
