Class 10 Math Chapter 6 Triangles Ex 6.4 NCERT Solutions is based on the application of similar triangles to prove the Pythagoras Theorem and its converse. This exercise builds on the similarity criteria learned in earlier exercises and uses them to derive important geometric results. Students will learn how to relate sides and angles of right-angled triangles using similarity and logical reasoning. The questions in this exercise are vital for strengthening geometric proof skills and are commonly asked in exams. These step-by-step NCERT solutions help in developing a strong foundation in geometry.
Class 10 Math Chapter 6 Triangles Ex 6.4 NCERT Textbook Solution
Ex 6.4 Class 10 Maths Question 1.
Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Solution: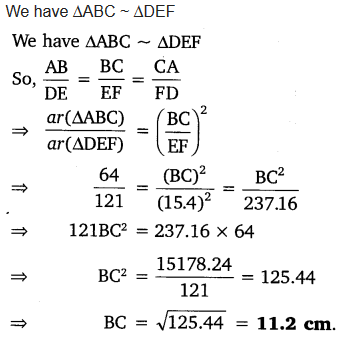
Ex 6.4 Class 10 Maths Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution: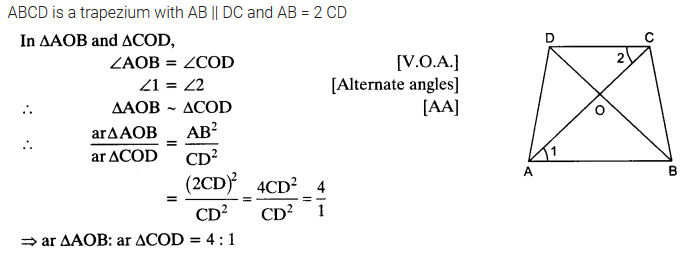
Ex 6.4 Class 10 Maths Question 3.
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that: Ar ABC/Ar DBC=AO/DO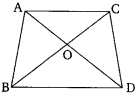
Solution: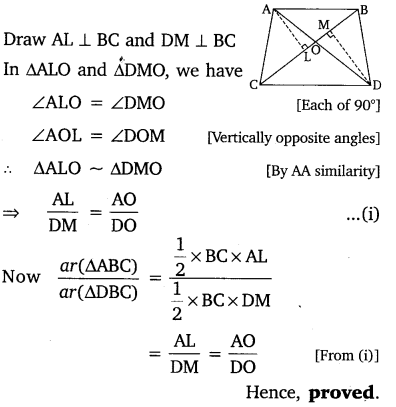
Ex 6.4 Class 10 Maths Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution: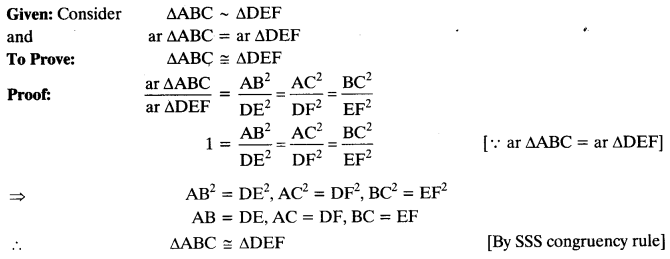
Ex 6.4 Class 10 Maths Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution: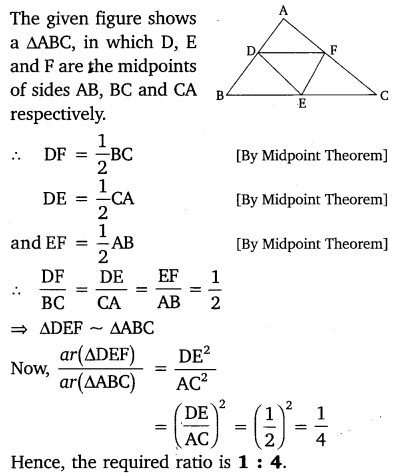
Ex 6.4 Class 10 Maths Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
Ex 6.4 Class 10 Maths Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution: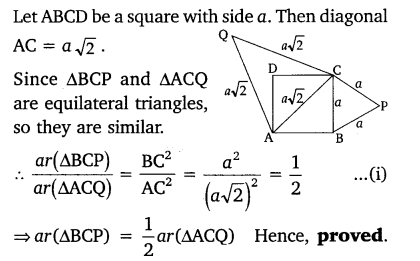
Ex 6.4 Class 10 Maths Question 8.
Tick the correct answer and justify
(i) ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(a) 2 :1
(b) 1:2
(c) 4 :1
(d) 1:4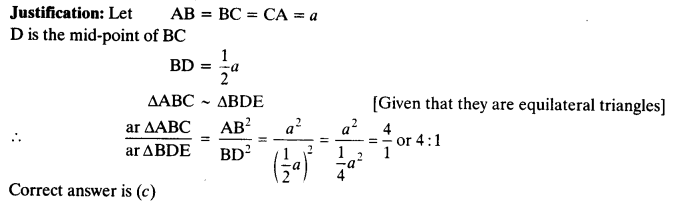
(ii) Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3
(b) 4 : 9
(c) 81 : 16
(d) 16 : 81
You can access the official NCERT Solutions for Class 10 Mathematics on the NCERT website at the following link:
NCERT Class 10 Mathematics Solutions
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
Class-wise Solutions
Class 12:
Class 12 Physics – NCERT Solutions
Class 12 Chemistry – NCERT Solutions
Class 11:
- Class 11 Physics – NCERT Solutions
- Class 11 Chemistry – NCERT Solutions
- Class 11 Biology – NCERT Solutions
- Class 11 Math – NCERT Solutions
Class 10:
Class 9:
Class 8:
Class 7:
Class 6:
Subject-wise Solutions
Physics:
Chemistry:
Biology:
Math:
- Class 11 Math – NCERT Solutions
- Class 10 Math – NCERT Solutions
- Class 9 Math – NCERT Solutions
- Class 8 Math – NCERT Solutions
Science:
- Class 10 Science – NCERT Solutions
- Class 9 Science – NCERT Solutions
- Class 8 Science – Oxford Solutions
- Class 7 Science – Oxford Solutions
- Class 6 Science – Oxford Solutions
