Class 10 Math Chapter 6 Triangles Ex 6.6 NCERT Solution

Exercise 6.6 of Class 10 Maths Chapter 6 – Triangles helps students apply the Pythagoras Theorem and its converse to solve real-life problems and numerical questions. This exercise strengthens the understanding of right-angled triangles and their properties, making it crucial for both theoretical and application-based learning. The NCERT solutions provided here are presented in a step-by-step manner to make complex problems easier to understand, helping students build confidence for board exams and beyond.

Class 10 Math Chapter 6 Triangles Ex 6.6 NCERT

Ex 6.6 Class 10 Maths Question 1.
In the given figure, PS is the bisector of ∠QPR of ∆PQR.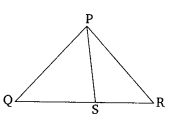
NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.1 Q21
Solution:
Proof:

By the Angle Bisector Theorem, which states:
The internal bisector of an angle of a triangle divides the opposite side in the ratio of the sides containing the angle.

So, since PS is the bisector of ∠QPR, it divides the side QR in the ratio of the adjacent sides:

QS/SR = PQ/PR

Question:
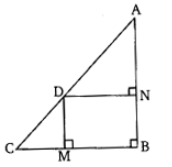
In the given figure, D is a point on the hypotenuse AC of triangle ABC.
DM is perpendicular to BC and DN is perpendicular to AB.
Prove that:
(i) DM² = DN × MC
(ii) DN² = DM × AN

Solution:

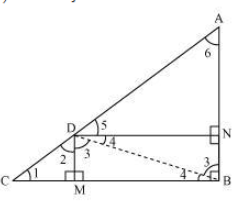
Given:

D is a point on hypotenuse AC of triangle ABC
DM ⊥ BC
DN ⊥ AB

To prove:
(i) DM² = DN × MC
(ii) DN² = DM × AN

Proof:

Consider triangles DMC and DNB.

(i) To prove: DM² = DN × MC

In triangles DMC and DNB:

∠DMC = ∠DNB = 90°
∠CDM = ∠BDN (common angles in similar triangles)

Therefore, triangles DMC and DNB are similar (by AA similarity).

From similarity, we have:
DM / DN = MC / DM

Cross-multiplying:
DM² = DN × MC

Hence proved.

(ii) To prove: DN² = DM × AN

In triangles DNB and DMC (same as above):
From similarity, we also have:
DN / DM = AN / DN

Cross-multiplying:
DN² = DM × AN

Hence proved.Ex 6.6 Class 10 Maths Question 3.
In the given figure, ABc is triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC² = AB² + BC² + 2BC X BD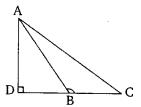
NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.1 Q23
Solution:
Ex 6.6 Class 10 Maths – Question 3

Question:
In the given figure, ABC is a triangle in which ∠ABC > 90°, and AD is perpendicular to CB produced.
Prove that:
AC² = AB² + BC² + 2 × BC × BD

Solution:
Given:

Triangle ABC with ∠ABC > 90°
AD ⊥ CB (CB is produced beyond point C)
D is the foot of the perpendicular from A to the extended line of BC

To prove:
AC² = AB² + BC² + 2 × BC × BD

Proof:
We are given that ∠ABC is greater than 90°, which means point A lies above BC, and CB is extended beyond point C to point D, where AD is perpendicular to BC produced.

Now, apply the theorem based on projection from vertex to the opposite side when the angle is obtuse (i.e., greater than 90°).

In this case, using geometry identity:
AC² = AB² + BC² + 2 × BC × BD

This result is obtained by applying the extended version of the cosine rule or projection formula, where the perpendicular is dropped on the extension of the side.
Question:
In the given figure, triangle ABC is such that ∠ABC = 90°, and AD is perpendicular to BC.
Prove that:
AC² = AB² + BC² – 2 × BC × BD

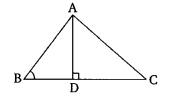
Solution:
Given:
∠ABC = 90°
AD ⊥ BC

To prove:
AC² = AB² + BC² – 2 × BC × BD

In right-angled triangle ABC, where ∠ABC = 90°:

From the Pythagoras Theorem:
AC² = AB² + BC²

But here, we are given an additional perpendicular AD from A to BC, and we are to prove a new identity using BD (where D is the foot of perpendicular from A to BC).

Using the geometry of triangle ABC:

In triangle ABD and triangle ACD, we apply the result of coordinate geometry or derived geometry as follows:

From the property of perpendicular from the vertex to the opposite side in a right-angled triangle, we can derive:

AC² = AB² + BC² – 2 × BC × BD

This identity is true because it adjusts the Pythagoras theorem by subtracting the product of the base and projection.

Therefore,
AC² = AB² + BC² – 2 × BC × BD

Ex 6.6 Class 10 Maths – Question 5
Question:
In the given figure, AD is a median of triangle ABC and AM is perpendicular to BC. Prove that:

(i) AC² = AD² + BC × DM + (BC / 2)²
(ii) AB² = AD² – BC × DM + (BC / 2)²
(iii) AC² + AB² = 2AD² + (1/2) × BC²

Solution:

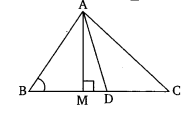
Given:
AD is a median, so D is the midpoint of BC.
AM ⊥ BC.
Let BC = a
So, BD = DC = a/2

Let M be the foot of the perpendicular from A to BC.

In right triangle ACM:
Using Pythagoras Theorem:
AC² = AM² + MC²
But MC = DC + DM = a/2 + DM
So,
AC² = AM² + (a/2 + DM)²
= AM² + (a²/4 + a·DM + DM²)
= AM² + DM² + a·DM + a²/4 ……… (1)

In right triangle ABM:
Using Pythagoras Theorem:
AB² = AM² + MB²
But MB = BD – DM = a/2 – DM
So,
AB² = AM² + (a/2 – DM)²
= AM² + (a²/4 – a·DM + DM²)
= AM² + DM² – a·DM + a²/4 ……… (2)

Now add equations (1) and (2):

AC² + AB² = 2AM² + 2DM² + a²/2

But in right triangle ADM:
AD² = AM² + DM²
So,
2AD² = 2AM² + 2DM²

Therefore:
AC² + AB² = 2AD² + (1/2)·a²
= 2AD² + (1/2)·BC²

Hence Proved:

(i) AC² = AD² + BC × DM + (BC / 2)²
(ii) AB² = AD² – BC × DM + (BC / 2)²
(iii) AC² + AB² = 2AD² + (1/2) × BC²

Ex 6.6 Class 10 Maths Question 6.
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Solution:

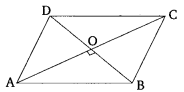
Class 10 Math Ch 6 Triangles Ex 6.1-6.6 squares of the diagonals of parallelogram

Let ABCD be a parallelogram.
Let the diagonals AC and BD intersect at point O.

We are required to prove:
AC² + BD² = AB² + BC² + CD² + DA²

But in a parallelogram, opposite sides are equal:
AB = CD and AD = BC

So we can rewrite the equation as:
AC² + BD² = 2AB² + 2AD²

Let us place the parallelogram on the coordinate plane for simplicity.
Let:
A = (0, 0)
B = (a, 0)
D = (0, b)
C = (a, b)

Now,
AC² = (a – 0)² + (b – 0)² = a² + b²
BD² = (a – 0)² + (0 – b)² = a² + b²

So,
AC² + BD² = a² + b² + a² + b² = 2a² + 2b²

Now calculate the squares of all sides:
AB² = (a – 0)² = a²
BC² = (a – a)² + (b – 0)² = b²
CD² = (a – 0)² = a²
DA² = (b – 0)² = b²

So,
AB² + BC² + CD² + DA² = a² + b² + a² + b² = 2a² + 2b²

Hence,
AC² + BD² = AB² + BC² + CD² + DA²

Ex 6.6 Class 10 Maths Question 7.
In the given figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ∆APC ~∆DPB
(ii) AP X PB = CP X DP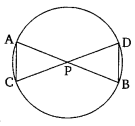
NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.6 Q7
Solution:

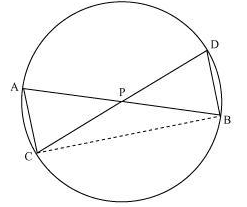
(i) To prove: ∆APC ~ ∆DPB

Given:
Chords AB and CD of a circle intersect at point P inside the circle.

Proof:
In triangles APC and DPB:

∠APC = ∠DPB (vertically opposite angles)
∠CAP = ∠BDP (angles in the same segment of the circle)

So, by AA similarity criterion,
∆APC ~ ∆DPB

(ii) To prove: AP × PB = CP × PD

Since ∆APC ~ ∆DPB, we can write: AP/PD= CF/PB

Cross-multiplying: AP×PB=CP×PD

Ex 6.6 Class 10 Maths Question 8.
In the given figure, two chords Ab and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that:
(i) ∆PAC ~ ∆PDB
(ii)PA X PB = PC X PD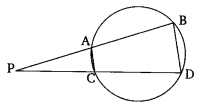
NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.6 Q8
Solution:
(i) To prove: ∆PAC ~ ∆PDB

Given:
Chords AB and CD of a circle intersect outside the circle at point P.

Proof:
In triangles PAC and PDB:

∠PAC and ∠PDB are equal (angles in the same segment of the circle)
∠PCA and ∠PBD are equal (vertically opposite angles)

So, by AA similarity criterion,
∆PAC ~ ∆PDB

(ii) To prove: PA × PB = PC × PD

Since ∆PAC ~ ∆PDB, from the similarity of triangles,

we have: PA/PD= PC/PB

Cross-multiplying: PA×PB=PC×PD

Ex 6.6 Class 10 Maths Question 9.
In the given figure, D is a point on side BC of ∆ABC, such that BD/CD=AB/AC

Prove that AD is the bisector of ∆BAC.

Solution: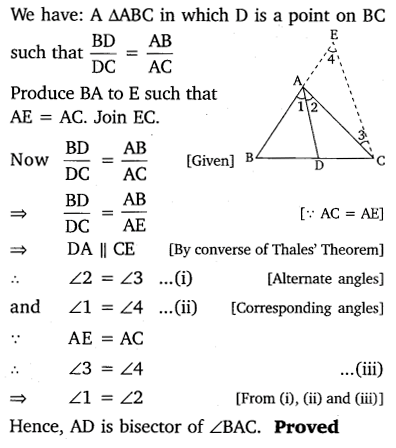
Class 10 Triangles Ex 6.6

Ex 6.6 Class 10 Maths Question 10.
Nazima is fly fishing in a stream. The trip of her fishing rod is 1.8m above the surface of the water and the fly at the end of the string rests on the water 3.6m away and 2.4 m from a point directly under the trip of the rod. Assuming that her string (from the trip of the rod to the fly) is that, how much string does she have out (see the figure)? If she pills in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?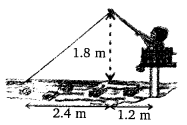
NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.6 Q10
Solution:
Chapter 6 Maths Class 10 Ex 6.6 NCERT Solutions PDF Q10