Class 11 Physics Work Energy Power Grade11 NCERT – Concept, notes

Work, Energy and Power is one of the most important chapters in Class 11 Physics Work Energy Power Grade11 NCERT. It builds the foundation for understanding motion, forces, and energy conservation – concepts that are used in higher studies and competitive exams.

Class 11 Physics Work Energy Power Grade11 NCERT - Concept, notes

This chapter in Class 11 Physics (NCERT/CBSE in India) and Grade 11 High School Physics (international curriculum) is crucial because:

It provides a connection between Newton’s laws of motion and the principle of conservation of energy.

It introduces the Work-Energy Theorem, a central law of mechanics.

It demonstrates how energy can take different forms while total energy remains conserved.

It explains the difference between conservative forces like gravity and non-conservative forces like friction.

It introduces the concept of power, which connects physics with engineering and daily life.

Class 11 Physics Work Energy Power Grade11 NCERT (Concepts, Notes & Solutions)

NCERT Class 11 Physics Work, Energy and Power notes with detailed explanations for CBSE students in India and Grade 11 high school learners worldwide.

1. Introduction

Physics is the study of matter, motion, and energy. Among its most powerful ideas are the concepts of work, energy, and power. These three terms are not only mathematical but also deeply intuitive because they describe everyday experiences. Every time you push a door, lift a bag, run up the stairs, or ride a bicycle, you are performing work, transferring energy, and consuming power.

By the end of this chapter, students should be able to calculate work done by forces, evaluate changes in energy, analyze energy conservation in systems, and understand the physical meaning of power.

2. Work

2.1 Definition

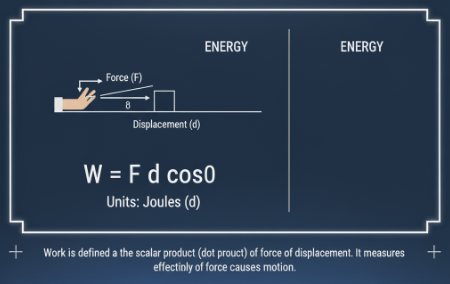
work defination

Work is defined as the scalar product (dot product) of force and displacement. It measures how effectively a force causes motion.

Formula:
W = F d cosθ

where F is the magnitude of force, d is displacement, and θ is the angle between them.

Work is a scalar quantity because it results from the dot product of two vectors.

2.2 Conditions for Work

  • A force must be applied.
  • The object must undergo displacement.
  • A component of the force must act along the displacement.

If displacement is zero, no work is done even if force is applied.

2.3 Types of Work

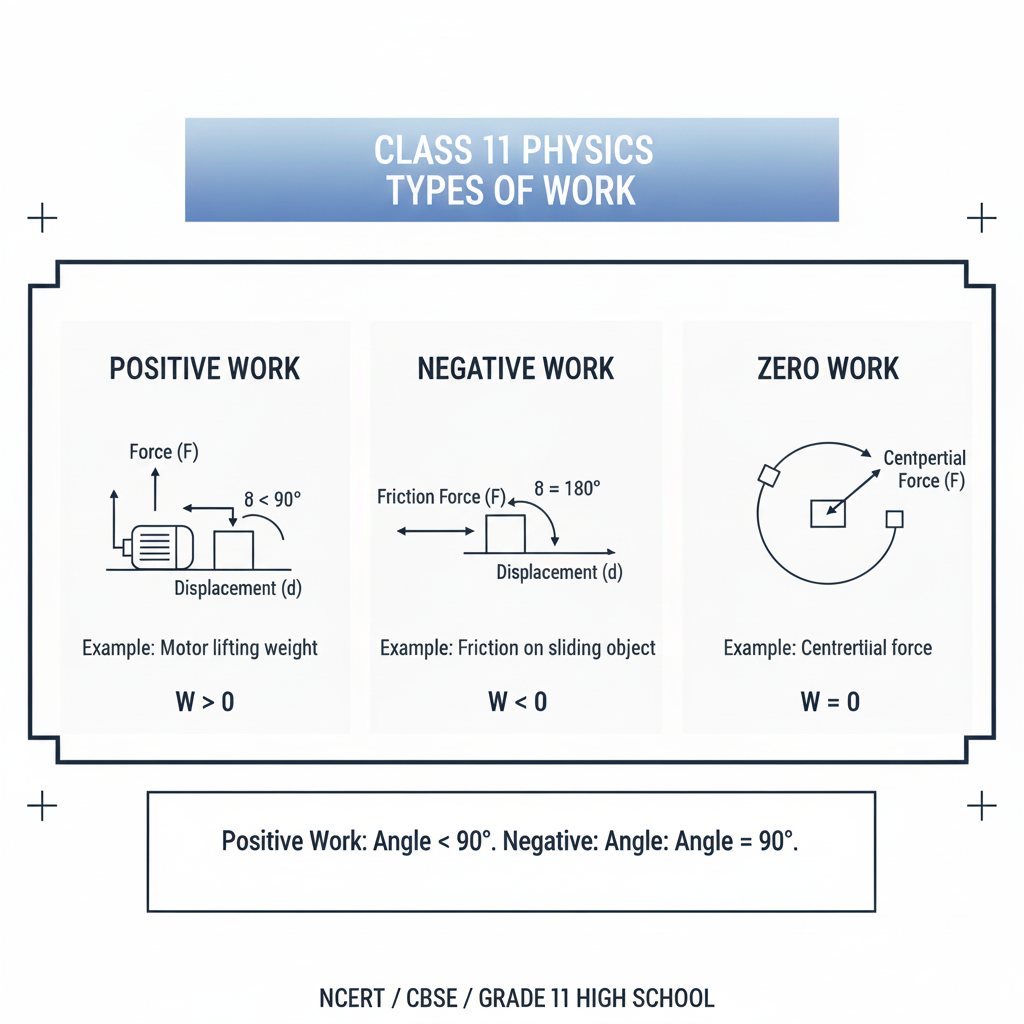
Types of Work

Positive Work: When the angle between force and displacement is less than 90°, work is positive. Example: Work done by a motor lifting a weight.

Negative Work: When force opposes displacement, work is negative. Example: Work done by friction on a sliding object.

Zero Work: When force is perpendicular to displacement. Example: Centripetal force in uniform circular motion.

2.4 Work Done by a Constant Force

If the force is constant and acts at an angle θ with displacement:
W = F d cosθ

2.5 Work Done by a Variable Force

When force changes with position, work is the integral of force over displacement:
W = ∫ F(x) dx

This is important in cases like stretching or compressing springs, or in fields where forces vary with position.

2.6 Work Done by Multiple Forces

When more than one force acts on a body, the net work done is the sum of the work done by each force.

W_total = W1 + W2 + W3 + …

This allows analysis of systems with applied forces, gravity, and friction simultaneously.

2.7 Units and Dimensions

  • SI Unit: Joule (J).
  • 1 J = Work done by a force of 1 Newton displacing an object by 1 meter in the direction of the force.
  • Dimensions: [M¹ L² T⁻²].

3. Energy

Energy is the capacity to do work. It exists in many forms such as mechanical, thermal, chemical, nuclear, and electrical. In mechanics, the two most relevant forms are kinetic energy and potential energy.

3.1 Kinetic Energy (KE)

Kinetic energy is the energy possessed by a body due to motion.

KE = ½ m v²

This shows that kinetic energy increases with the square of velocity. A car moving at double speed has four times the kinetic energy.

3.2 Potential Energy (PE)

Potential energy is the energy possessed by a body due to its position or configuration.

  • Gravitational PE: PE = m g h
  • Elastic PE (spring): U = ½ k x²

Potential energy is associated with conservative forces.

3.3 Work-Energy Theorem

The net work done on an object is equal to the change in its kinetic energy.

W_net = ΔKE = KE_final − KE_initial

This theorem directly connects Newton’s second law with the concept of energy.

3.4 Conservation of Mechanical Energy

In the absence of non-conservative forces, the total mechanical energy (kinetic + potential) remains constant.

KE + PE = constant

Examples include pendulums, roller coasters, and planetary motion.

4. Power

4.1 Definition

Power is the rate at which work is done.

P = W / t

If a constant force F acts on a body moving with velocity v in the same direction:
P = F v

4.2 Units

  • SI Unit: Watt (W).
  • 1 Watt = 1 Joule per second.
  • Commercial Unit: kilowatt hour (kWh) = 1000 W × 3600 s = 3.6 × 10⁶ J.

4.3 Average and Instantaneous Power

  • Average Power = Total work done / Total time.
  • Instantaneous Power = F · v at any instant.

Power is especially important in engineering because it shows how fast energy is delivered.

5. Conservative and Non-Conservative Forces

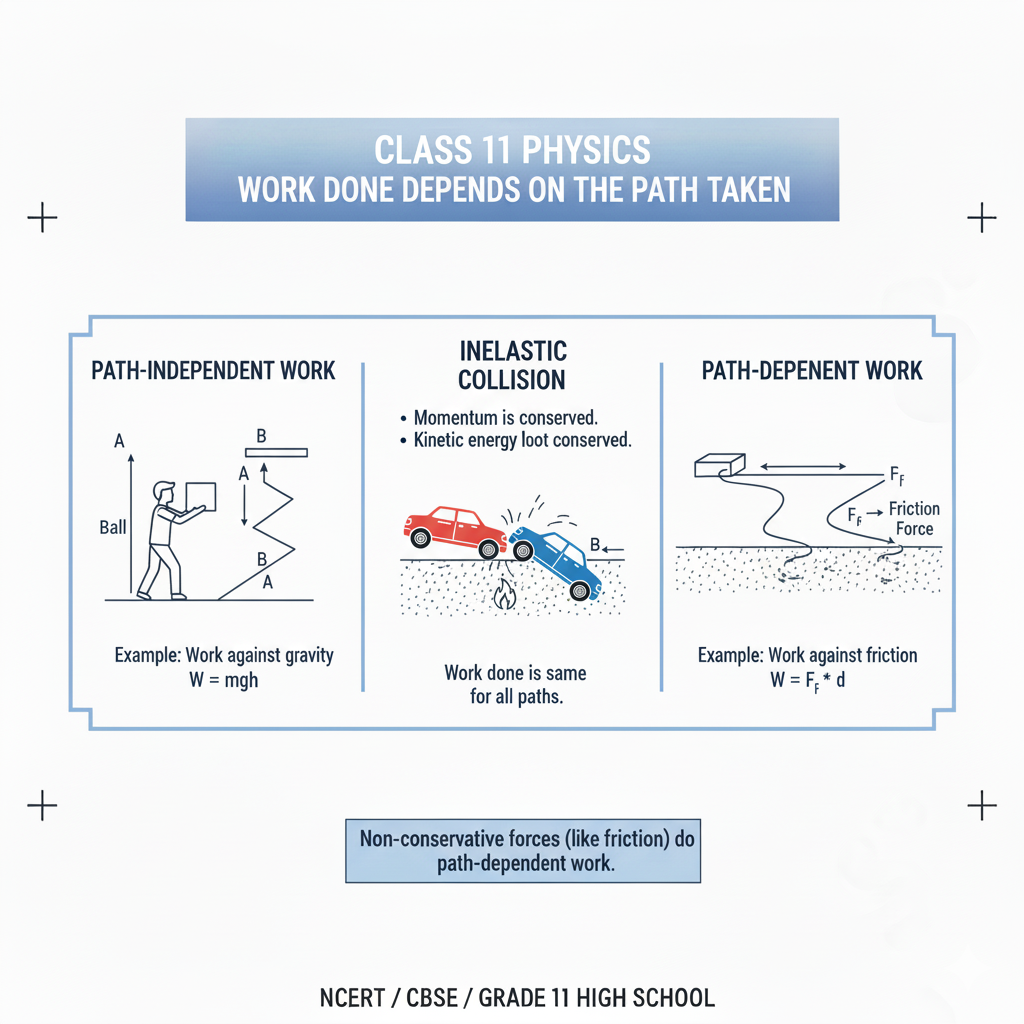
5.1 Conservative Forces

A force is conservative if:

  • Work done is path-independent.
  • Work done in a closed loop is zero.
  • A potential energy function can be defined.

Examples: gravitational force, electrostatic force, spring force.

5.2 Non-Conservative Forces

A force is non-conservative if:

  • Work done depends on the path taken.
  • Energy is dissipated as heat or sound.
  • No potential energy function exists.

Examples: friction, air resistance

6. Collisions

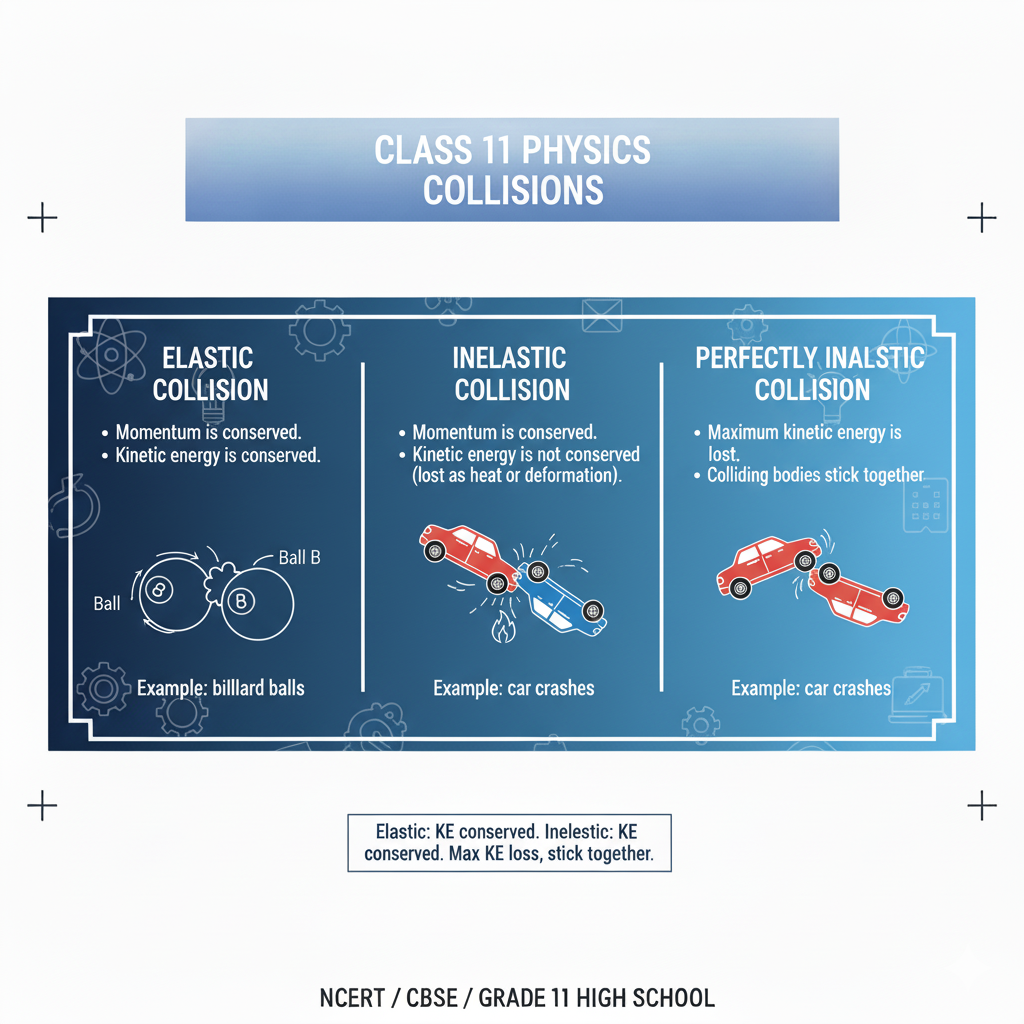
Collisions are interactions between bodies where they exert forces on each other for short durations.

6.1 Elastic Collision

  • Momentum is conserved.
  • Kinetic energy is conserved.
  • Example: collisions of billiard balls, gas molecules.

6.2 Inelastic Collision

  • Momentum is conserved.
  • Kinetic energy is not conserved (lost as heat or deformation).
  • Example: car crashes.

6.3 Perfectly Inelastic Collision

  • Maximum kinetic energy is lost.
  • Colliding bodies stick together.

6.4 Equations for One-Dimensional Elastic Collision

Formulas for One-Dimensional Elastic Collision

For two bodies of masses m₁ and m₂, moving with initial velocities v₁ and v₂ before collision, the final velocities after an elastic collision are:

  • Velocity of first body after collision (v₁′):

v₁′ = [(m₁ − m₂) / (m₁ + m₂)] × v₁ + [2m₂ / (m₁ + m₂)] × v₂

  • Velocity of second body after collision (v₂′):

v₂′ = [2m₁ / (m₁ + m₂)] × v₁ + [(m₂ − m₁) / (m₁ + m₂)] × v₂

7. Applications of Work, Energy, and Power

Applications of Work, Energy, and Power

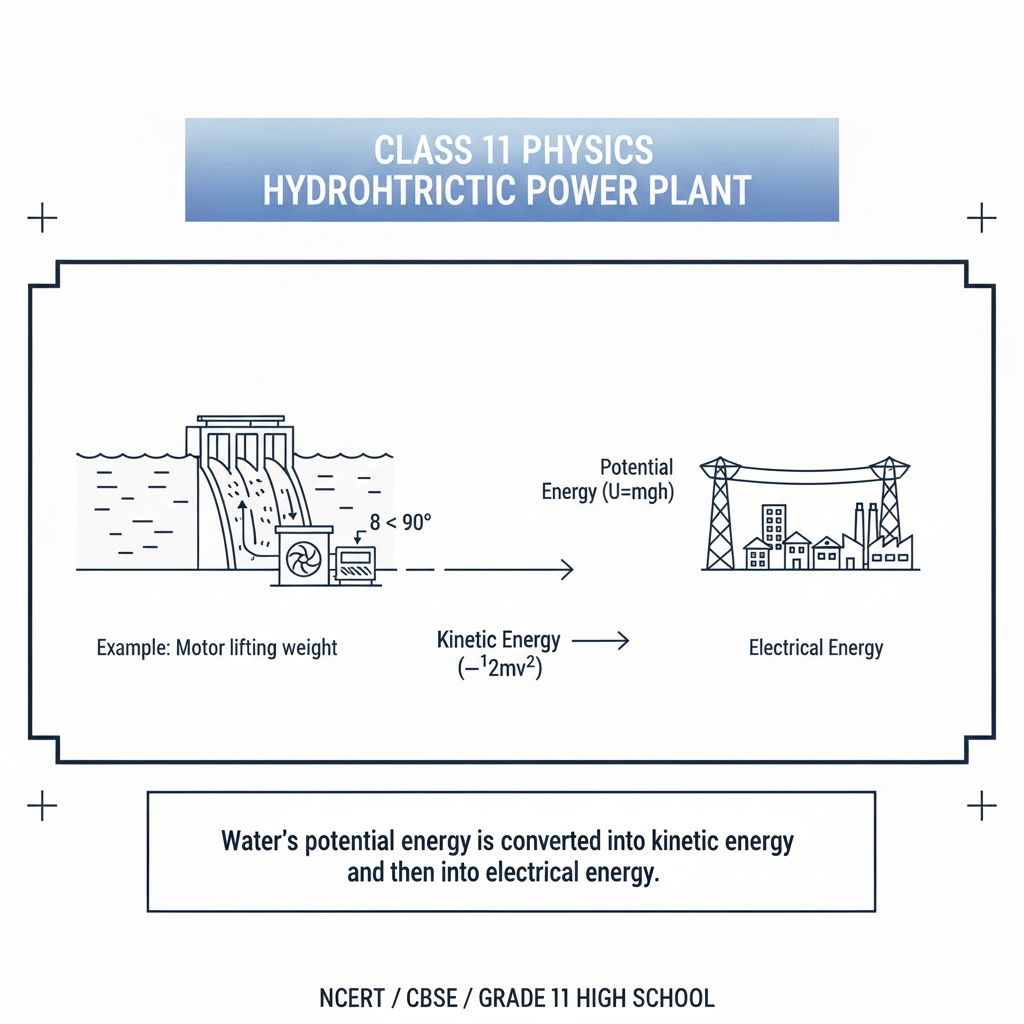
Work, energy, and power principles explain countless phenomena:

Machines: Efficiency depends on how much input work is converted into useful output.

Hydroelectric power plants: Water’s potential energy is converted into kinetic energy and then into electrical energy.

Automobiles: Chemical energy of fuel is converted into mechanical energy.

Sports: Kinetic energy of moving players and balls determines outcomes.

Weightlifting: Work done against gravity.

Electrical appliances: Power rating indicates energy consumption.

Satellites: Centripetal force does no work, keeping energy constant in orbit.

8. Important Formulas

  1. Work = F d cosθ
  2. Kinetic Energy = ½ m v²
  3. Potential Energy = m g h
  4. Work-Energy Theorem: W_net = ΔKE
  5. Power = W / t = F v
  6. Spring Potential Energy = ½ k x²
  7. Elastic collision formulas (1D)
  8. 1 kWh = 3.6 × 10⁶ J

Class 11 Physics Work Energy Power Grade11 NCERT – Exercise Questions

Part A: NCERT Exercise Questions (Q.5.1 – Q.5.33)
These are the official questions from the NCERT textbook.

Part B: Additional Practice Questions (Q.5.34 – Q.5.90)
These questions are not part of NCERT, but for you as extra practice.
They can be useful for:

  • Strengthening conceptual understanding.
  • Preparing for competitive exams (like JEE/NEET).
  • Extra revision beyond NCERT.
  1. NCERT Exercise Solutions (Q.5.1 – Q.5.33)
  2. Additional Practice Problems with Solutions (Q.5.34 – Q.5.90)

Class 11 Physics Work Energy Power Grade11 NCERT (Q.5.1 – Q.5.33)

Q.5.1 State, with reasons, whether the following algebraic sums of work are positive, negative or zero:
(a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) Work done by the gravitational force in the above case.
(c) Work done by the friction on a body sliding down an inclined plane.
(d) Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
(e) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Answer:
(a) Positive — force (upward) and displacement (upward) are in the same direction.
(b) Negative — gravitational force downward, displacement upward (opposite).
(c) Negative — friction opposes motion (opposite displacement).
(d) Applied force does positive work; net work is zero because velocity is constant (ΔK = 0).
(e) Negative — resistive force opposes motion and removes mechanical energy as heat.

Q.5.2 A body of mass 2 kg is initially at rest on a horizontal table. It is acted upon by an applied horizontal force of 7 N. The coefficient of kinetic friction between the body and the table is 0.1. Find the work done by the applied force, the frictional force, and the net force on the body during the first 10 s, and also the change in kinetic energy during this period. (Use g = 9.8 m/s².)
Answer:
Friction f = μkg = 0.1×2×9.8 = 1.96 N.
Net force F_net = 7 − 1.96 = 5.04 N.
Acceleration a = 5.04 / 2 = 2.52 m/s².
Displacement in 10 s: s = ½ a t² = 0.5×2.52×100 = 126 m.
Work by applied force = 7 × 126 = 882 J.
Work by friction = −1.96 × 126 ≈ −246.96 J (≈ −247 J).
Work by net force = 5.04 × 126 = 635.04 J.
Change in kinetic energy = ½ m v² = 635.04 J.

Q.5.3 Given below are examples of potential energy functions in one dimension. For each case, sketch the graph and indicate the regions of motion which are classically allowed or forbidden for a particle of energy E.
Answer: Motion is classically allowed where V(x) ≤ E (kinetic energy ≥ 0). Regions with V(x) > E are forbidden. Turning points occur where V(x) = E.

Q.5.4 The potential energy function for a particle executing simple harmonic motion is V(x) = ½ k x². If the total energy of the particle is 1 J and k = 0.5 N/m, find the maximum displacement of the particle.
Answer: V(x) = 0.25 x². Set 0.25 x² = 1 → x² = 4 → x = ±2 m. Maximum displacement = 2 m.

Q.5.5 (a) A rocket burns up in atmosphere due to friction. Where does this heat energy come from? (b) A comet travels around the Sun in an elliptical orbit. Is the gravitational force doing net work on it?
Answer: (a) Heat comes from the rocket’s mechanical energy (kinetic and internal/chemical) converted to heat by air friction. (b) Over a complete orbit gravitational force does zero net work (it is conservative) — KE and PE exchange but total mechanical energy remains constant (neglecting non-gravitational forces).

Q.5.6 Choose the correct alternative:
(a) When a conservative force does positive work on a body, the potential energy (increases / decreases / remains unchanged).
(b) Work done against friction is in the form of (kinetic / potential / mechanical / heat) energy.
(c) If the rate of change of momentum is zero, the external force is (zero / finite / non-zero).
(d) In an elastic collision, both kinetic energy and (linear momentum / angular momentum / total energy) are conserved.
Answer: (a) Decreases. (b) Heat. (c) Zero. (d) Linear momentum (and total mechanical energy).

Q.5.7 State True or False:
(a) In an elastic collision, both momentum and kinetic energy of each body are conserved.
(b) If the external force on a system is zero, its total mechanical energy is always conserved.
(c) The work done by a force in moving a particle over a closed loop is zero.
(d) In an inelastic collision, the final kinetic energy is less than the initial kinetic energy of the system.
Answer: (a) False. (b) False. (c) False (only true for conservative forces). (d) True.

Q.5.8 Answer the following:
(a) Is kinetic energy of each body conserved during collision?
(b) Is momentum of each body conserved during collision?
(c) Is kinetic energy conserved in inelastic collision?
(d) What type of force ensures that a collision is elastic?
Answer: (a) No. (b) No (only total momentum conserved). (c) No. (d) Conservative forces (derived from a potential depending only on separation).

Q.5.9 A body starts from rest under uniform acceleration. The power delivered to it at time t is proportional to (i) t⁰, (ii) t, (iii) t², (iv) t³.
Answer: Power P = F·v = ma·(at) = m a² t → proportional to t (option ii).

Q.5.10 A body moves under the action of a constant power source. Its displacement in time t varies as (i) t^{1/2}, (ii) t, (iii) t^{3/2}, (iv) t².
Answer: With constant power P, ½ m v² = P t → v ∝ t^{1/2}; s ∝ t^{3/2} → option (iii).

Q.5.11 A block of mass 0.5 kg is attached to a spring of k = 200 N/m. Pulled to 0.1 m and released. Find potential energy stored and maximum speed.
Answer: U = ½ k x² = 1.0 J. v_max = √(2U/m) = √(2×1 / 0.5) = 2.0 m/s.

Q.5.12 A constant force F = 10 N acts on a 2 kg particle initially at rest. How much work is done in moving the particle through 5 m? What is the KE after this displacement?
Answer: Work = F s = 10×5 = 50 J. KE = 50 J.

Q.5.13 A force F(x) = 4x N acts on a particle along x-axis. Calculate work done from x = 0 to x = 3 m.
Answer: W = ∫₀³ 4x dx = 18 J.

Q.5.14 Pendulum bob m = 0.2 kg, l = 1.5 m pulled to 30°. Find loss in PE when it passes lowest point and speed at lowest point.
Answer: h = l(1 − cos30°) = 0.201 m. ΔPE = m g h ≈ 0.394 J. v = √(2ΔPE/m) ≈ 1.99 m/s.

Q.5.15 Car m = 1000 kg, v = 20 m/s, stopped in 5 s. Find (a) average power delivered by brakes, (b) magnitude of braking force.
Answer: Initial KE = ½×1000×20² = 200,000 J. (a) Power = 200,000 / 5 = 40,000 W. (b) Deceleration a = −20/5 = −4 m/s² → F = m a = −4000 N (magnitude 4000 N).

Q.5.16 Two particles, each mass 1 kg, move towards each other at 3 m/s and 2 m/s and stick. Find loss of KE.
Answer: Initial KE = ½(1×3²) + ½(1×2²) = 6.5 J. Total momentum = 1 kg·m/s → combined v = 0.5 m/s → Final KE = ½×2×0.5² = 0.25 J. Loss = 6.5 − 0.25 = 6.25 J.

Q.5.17 Force (3i + 4j) N acts as particle moves from (0,0) to (2,1). Find work done.
Answer: s = (2i + 1j). W = F·s = 3×2 + 4×1 = 10 J.

Q.5.18 Block 4 kg pulled up frictionless incline to height 3 m by a force doing 200 J of work. Final speed?
Answer: m g h = 4×9.8×3 = 117.6 J. KE = 200 − 117.6 = 82.4 J → ½ m v² = 82.4 → v ≈ 6.42 m/s.

Q.5.19 Cyclist (total mass 70 kg) rides up 50 m at constant speed. Power = 250 W. Time to climb?
Answer: Work = m g h = 70×9.8×50 = 34,300 J. Time = 34,300 / 250 ≈ 137.2 s ≈ 137 s.

Q.5.20 V(x) = 8 − 2x² (J). Total energy E = 6 J. Find turning points and classically allowed region.
Answer: 8 − 2x² = 6 → x² = 1 → x = ±1 m. Allowed regions where V ≤ E ⇒ x² ≥ 1 → x ≤ −1 or x ≥ +1. Forbidden: −1 < x < 1.

Q.5.21 F(x) = 6x² N. Work from x = 0 to x = 2 m?
Answer: W = ∫₀² 6x² dx = 16 J.

Q.5.22 m = 0.2 kg, spring k = 50 N/m stretched by x = 0.05 m. Find U and v_max.
Answer: U = ½ k x² = 0.0625 J. v_max = √(2U/m) ≈ 0.79 m/s.

Q.5.23 Block 3 kg pulled up rough incline to height 1.2 m at constant speed. Applied work = 100 J. Work done by friction?
Answer: ΔU = m g h = 3×9.8×1.2 = 35.28 J. W_fric = W_applied − ΔU = 100 − 35.28 = 64.72 J (friction does −64.72 J).

Q.5.24 Constant horizontal force F = 20 N pulls body with constant speed v = 5 m/s. Power delivered?
Answer: P = F v = 20 × 5 = 100 W.

Q.5.25 Elastic collision: m1 = 2 kg, v1 = 5 m/s; m2 = 3 kg, v2 = −2 m/s. Find v1′ and v2′.
Answer: v1′ = −3.4 m/s, v2′ = 3.6 m/s.

Q.5.26 Car mass 800 kg accelerates from 10 to 25 m/s. Net work done?
Answer: ΔK = ½ m (v² − u²) = 0.5×800×(625 − 100) = 210,000 J.

Q.5.27 V(x) = −4/x (x > 0). (a) Find F(x). (b) Work from x = 1 to x = 2.
Answer: (a) F(x) = −dV/dx = −4/x². (b) Work = −ΔV = −(V(2) − V(1)) = −(−2 − (−4)) = −2 J.

Q.5.28 m = 0.5 kg, power P(t) = 3t W, starts from rest. Find speed at t = 4 s.
Answer: d(v²)/dt = 2P/m → integrate: v² = ∫ (2P/m) dt = ∫ (2×3t / 0.5) dt = ∫ 12 t dt = 6 t². So v = √(6) t. At t=4, v = 4√6 ≈ 9.80 m/s.

Q.5.29 m = 0.5 kg, spring k = 8 N/m, at equilibrium speed v₀ = 2 m/s. Find amplitude A.
Answer: Initial energy = ½ m v₀² = 1.0 J = ½ k A² → A² = 2 / k = 2/8 = 0.25 → A = 0.5 m.

Q.5.30 Mass 2 kg, circular track r = 0.5 m, v = 3 m/s, tangential resistive force 2 N. (a) Power to maintain speed? (b) Work done against friction per revolution?
Answer: (a) P = F v = 2 × 3 = 6 W. (b) Circumference = 2πr = π m. Time per rev T = distance / v = π / 3. Work per rev = P × T = 6 × (π/3) = 2π ≈ 6.283 J.

Q.5.31 F(x) = 2x³ N. Work from x = 0 to x = 1 m?
Answer: W = ∫₀¹ 2x³ dx = 0.5 J.

Q.5.32 m = 0.4 kg, spring k = 200 N/m stretched x = 0.2 m and released. (a) U? (b) v_max?
Answer: U = ½ k x² = 4.0 J. v_max = √(2U/m) = √(8 / 0.4) = √20 ≈ 4.47 m/s.

Q.5.33 A man lifts m = 50 kg vertically through h = 2 m at constant speed. Find work done. (Take g = 9.8 m/s².)
Answer: Work = m g h = 50 × 9.8 × 2 = 9,800 J.

Additional Practice Questions Class 11 Physics Work Energy Power Grade11 NCERT (Q.5.34 – Q.5.90)

(For NCERT/CBSE students in India and international learners preparing for Physics exams or practice.)

Q.5.34 A force of magnitude 15 N acts at an angle 60° above the horizontal and moves its point of application through 3 m horizontally. Find the work done by the force.
Answer:
Horizontal component of force = 15 cos60° = 15 × 0.5 = 7.5 N.
Work done = 7.5 × 3 = 22.5 J.

Q.5.35 Two particles undergo a one-dimensional elastic head-on collision. m₁ = 1 kg with v₁ = 4 m/s (to the right) and m₂ = 2 kg with v₂ = 0. Find their velocities after the collision.
Answer:
Using elastic collision formulas:
v₁′ = [(m₁ − m₂) / (m₁ + m₂)] v₁ + [2m₂ / (m₁ + m₂)] v₂
= (1 − 2)/3 × 4 + (4/3) × 0 = −4/3 = −1.333 m/s.

v₂′ = [2m₁ / (m₁ + m₂)] v₁ + [(m₂ − m₁) / (m₁ + m₂)] v₂
= (2/3) × 4 + (1/3) × 0 = 8/3 = 2.667 m/s.

Q.5.36 A particle of mass 2 kg moves from point A at height yA = 5 m to point B at height yB = 2 m. Find the work done by gravity. (Take g = 9.8 m/s².)
Answer:
Work by gravity = m g (yA − yB) = 2 × 9.8 × (5 − 2) = 58.8 J.
(Positive, because displacement is downward and gravity does positive work.)

Q.5.37 Water of mass 200 kg is to be pumped vertically up by 10 m in 50 s. What minimum power is required (ignore losses)? (Take g = 9.8 m/s².)
Answer:
Work (energy required) = m g h = 200 × 9.8 × 10 = 19,600 J.
Power = Work / time = 19,600 / 50 = 392 W.

Q.5.38 For the potential V(x) = x⁴ − 2x² (energy in J), find the equilibrium points and classify each as stable or unstable.
Answer:
dV/dx = 4x³ − 4x = 4x(x² − 1) = 0 → x = 0, ±1.
d²V/dx² = 12x² − 4.
At x = 0, d²V/dx² = −4 (< 0) → unstable (local maximum).
At x = ±1, d²V/dx² = 8 (> 0) → stable (local minima).

Q.5.39 A block of mass 0.2 kg moving with speed 3 m/s compresses a spring (stiffness k = 200 N/m) and comes to rest. Find the compression.
Answer:
Initial KE = ½ m v² = 0.5 × 0.2 × 9 = 0.9 J.
Spring PE = ½ k x² = 0.9 → x² = 1.8 / 200 = 0.009.
x = √0.009 ≈ 0.095 m.

Q.5.40 A body of mass 10 kg is acted on by a constant power source P = 500 W. If it starts from rest, find its speed after t = 4 s.
Answer:
½ m v² = P t → v = √(2 P t / m).
= √(2 × 500 × 4 / 10) = √400 = 20 m/s.

Q.5.51 A spring of force constant k = 200 N/m is compressed by 5 cm. Find the potential energy stored in the spring.
Answer:
U = ½ k x² = 0.5 × 200 × (0.05)² = 100 × 0.0025 = 0.25 J.

Q.5.52 A body of mass 4 kg moving with speed 6 m/s comes to rest under a constant force after moving through 9 m. Find the force.
Answer:
Initial KE = ½ m v² = 0.5 × 4 × 36 = 72 J.
Work = Force × distance = −72 J.
F × 9 = −72 → F = −8 N. (Magnitude = 8 N opposite to motion.)

Q.5.53 A block of mass 10 kg slides down a smooth inclined plane of height 5 m. Find its velocity at the bottom. (Take g = 9.8 m/s².)
Answer:
Loss in PE = Gain in KE = m g h = 10×9.8×5 = 490 J.
½ m v² = 490 → 5 v² = 490 → v² = 98 → v ≈ 9.9 m/s.

Q.5.54 A car of mass 1200 kg is moving at 20 m/s. Find the kinetic energy of the car.
Answer:
KE = ½ m v² = 0.5 × 1200 × (20)² = 600 × 400 = 240,000 J.

Q.5.55 A machine raises a load of 150 kg to a height of 40 m in 30 s. Calculate the power of the machine. (Take g=9.8 m/s².)
Answer:
Work = m g h = 150 × 9.8 × 40 = 58,800 J.
Power = Work/time = 58,800 / 30 = 1,960 W ≈ 1.96 kW.

Q.5.56 A force of 100 N moves a body through 5 m. If the angle between force and displacement is 37°, find the work done.
Answer:
W = F s cosθ = 100 × 5 × cos37°. cos37° ≈ 0.8.
So W = 500 × 0.8 = 400 J.

Q.5.57 A stone of mass 2 kg is thrown vertically upwards with speed 10 m/s. Find the maximum height reached. (Take g=9.8 m/s².)
Answer:
Initial KE = ½ m v² = 1 × 100 = 100 J.
At maximum height, KE = 0, all energy is PE.
m g h = 100 → 2 × 9.8 × h = 100 → h = 100 / 19.6 ≈ 5.10 m.

Q.5.58 A block of mass 0.5 kg slides on a horizontal surface with initial velocity 4 m/s and comes to rest after 8 m. Find the frictional force.
Answer:
Initial KE = ½ m v² = 0.25 × 16 = 4 J.
Work by friction = −F × d = −4 J.
F × 8 = 4 → F = 0.5 N.

Q.5.59 A 2 kg body is acted upon by a constant power source of 40 W. If it starts from rest, find its velocity after 5 s.
Answer:
½ m v² = P t → v = √(2 P t / m).
= √(2×40×5 / 2) = √(200/2) = √100 = 10 m/s.

Q.5.60 A block of mass 5 kg falls freely from rest from a height of 20 m. Find its speed just before striking the ground. (Take g=9.8 m/s².)
Answer:
Loss in PE = Gain in KE.
m g h = ½ m v² → 9.8 × 20 = ½ v² → 196 = 0.5 v² → v² = 392 → v ≈ 19.8 m/s.

Q.5.61 A constant force of 25 N displaces a body through 4 m in the direction of the force. Find the work done.
Answer:
W = F × d = 25 × 4 = 100 J.

Q.5.62 A mass of 0.1 kg is attached to a spring of constant 20 N/m. The spring is stretched by 0.05 m. Find the potential energy stored in the spring.
Answer:
U = ½ k x² = 0.5 × 20 × (0.05)² = 10 × 0.0025 = 0.025 J.

Q.5.63 A bullet of mass 0.01 kg moving with velocity 200 m/s penetrates 5 cm into a fixed wooden block. Find the average resistive force exerted by the block.
Answer:
Initial KE = ½ m v² = 0.5 × 0.01 × (200)² = 0.005 × 40,000 = 200 J.
Work done by resistive force = −F × d = −200 J.
F × 0.05 = 200 → F = 200 / 0.05 = 4000 N.

Q.5.64 A pump raises 500 kg of water per minute from a well of depth 10 m. Find the power required. (Take g = 9.8 m/s².)
Answer:
Mass per second = 500/60 ≈ 8.33 kg/s.
Power = m g h per second = 8.33 × 9.8 × 10 ≈ 816 W.

Q.5.65 A block of mass 2 kg slides down a smooth incline of height 1.25 m. Find the velocity at the bottom. (g = 9.8 m/s².)
Answer:
m g h = ½ m v² → v = √(2 g h) = √(2 × 9.8 × 1.25) = √24.5 ≈ 4.95 m/s.

Q.5.66 A 1000 kg car moving at 20 m/s is stopped by brakes in 5 s. Find the average braking force.
Answer:
Deceleration a = Δv/Δt = −20/5 = −4 m/s².
Force = m a = 1000 × (−4) = −4000 N. Magnitude = 4000 N.

Q.5.67 A force of 12 N displaces a body by 2 m. The angle between force and displacement is 30°. Find the work done.
Answer:
W = F s cosθ = 12 × 2 × cos30° = 24 × 0.866 ≈ 20.8 J.

Q.5.68 A stone of mass 0.5 kg falls freely from a height of 10 m. Find the work done by gravity and KE just before hitting the ground. (g = 9.8 m/s².)
Answer:
Work by gravity = m g h = 0.5 × 9.8 × 10 = 49 J.
Kinetic energy just before ground = 49 J.

Q.5.69 A machine raises a load of 600 N through 20 m in 30 s. Calculate the power.
Answer:
Work = F × d = 600 × 20 = 12,000 J.
Power = Work/time = 12,000 / 30 = 400 W.

Q.5.70 A body of mass 5 kg is acted upon by a constant power of 200 W. If it starts from rest, find its speed after 10 s.
Answer:
½ m v² = P t → v = √(2 P t / m).
= √(2 × 200 × 10 / 5) = √(4000/5) = √800 ≈ 28.3 m/s.

Q.5.81 A constant force of 50 N displaces a body by 6 m in the direction of force. Find the work done.
Answer: W = F × d = 50 × 6 = 300 J.

Q.5.82 A spring of constant k = 150 N/m is compressed by 0.1 m. Find the potential energy stored.
Answer: U = ½ k x² = 0.5 × 150 × 0.01 = 0.75 J.

Q.5.83 A body of mass 2 kg moving with velocity 8 m/s is brought to rest by a constant force in 4 m. Find the force.
Answer: Initial KE = ½ × 2 × 64 = 64 J. Work = –64 J. F × 4 = –64 → F = –16 N. Magnitude = 16 N.

Q.5.84 A block slides down a frictionless incline of vertical height 1.8 m. Find its velocity at the bottom. (g = 9.8 m/s²)
Answer: v = √(2 g h) = √(2 × 9.8 × 1.8) = √35.28 ≈ 5.94 m/s.

Q.5.85 A truck of mass 2000 kg is moving at 15 m/s. Find its kinetic energy.
Answer: KE = ½ m v² = 0.5 × 2000 × 225 = 1000 × 225 = 225,000 J.

Q.5.86 A machine raises 250 kg of water per minute to a height of 30 m. Calculate the power. (g = 9.8 m/s²)
Answer: Mass/sec = 250/60 = 4.17 kg/s.
Power = m g h per sec = 4.17 × 9.8 × 30 ≈ 1,225 W ≈ 1.23 kW.

Q.5.87 A force of 40 N displaces a body by 2.5 m at an angle of 60°. Find the work done.
Answer: W = F s cosθ = 40 × 2.5 × cos60° = 100 × 0.5 = 50 J.

Q.5.88 A stone of mass 0.4 kg is thrown vertically upward with speed 14 m/s. Find the maximum height reached. (g = 9.8 m/s²)
Answer: h = v² / (2g) = 196 / 19.6 = 10 m.

Q.5.89 A body of mass 3 kg is acted upon by constant power 150 W. If it starts from rest, find its speed after 6 s.
Answer: ½ m v² = P t → v = √(2Pt/m) = √(2 × 150 × 6 / 3) = √(600) ≈ 24.5 m/s.

Q.5.90 A block of mass 1.5 kg moving with velocity 4 m/s comes to rest after 6 m due to friction. Find the frictional force.
Answer: Initial KE = ½ × 1.5 × 16 = 12 J. Work = –12 J. F × 6 = –12 → F = –2 N. Magnitude = 2 N.

Worksheet: Work, Energy and Power

1. Definitions (Fill in the blanks)

  1. Work is said to be done when a __________ is applied and the body undergoes __________.
  2. The energy possessed by a body due to motion is called __________.
  3. The energy possessed by a body due to position is called __________.
  4. Power is the __________ of doing work.
  5. A force is called conservative if the work done is __________ of path.

2. True or False

  1. Work is a vector quantity.
  2. Work done by friction is always negative.
  3. Kinetic energy depends only on mass, not on velocity.
  4. Power is measured in Joules.
  5. In a perfectly inelastic collision, maximum kinetic energy is lost.

3. Short Answer Questions

  1. Write the SI unit and dimensions of work.
  2. State the Work-Energy Theorem.
  3. Give two examples of conservative forces.
  4. Differentiate between elastic and inelastic collisions.
  5. Why does centripetal force do no work?

4. Formula Practice (Write the correct formula)

  1. Work done by a constant force.
  2. Kinetic energy of a moving body.
  3. Potential energy of a body at height h.
  4. Power in terms of force and velocity.
  5. Potential energy stored in a spring.

5. Conceptual Questions

  1. Can a force do work without displacement? Why or why not?
  2. Why is work done against friction always negative?
  3. Explain why energy is said to be conserved in an isolated system.
  4. Why is momentum conserved in all types of collisions?
  5. What does the power rating of an electrical appliance indicate?

Summary: Work, Energy and Power

  • Work: Product of force and displacement in the direction of force.
    Formula: W = F d cosθ
  • Energy: Capacity to do work.
    • Kinetic Energy: KE = ½ m v²
    • Potential Energy: PE = m g h
    • Spring Energy: U = ½ k x²
  • Work-Energy Theorem: Net work done = Change in KE.
  • Conservation of Energy: Total mechanical energy (KE + PE) remains constant if only conservative forces act.
  • Power: Rate of doing work.
    Formula: P = W/t = F v
    Unit: Watt (W), 1 kWh = 3.6 × 10⁶ J
  • Conservative Forces: Path independent, work over closed path = 0 (e.g., gravity, spring).
  • Non-Conservative Forces: Path dependent, dissipate energy (e.g., friction, air resistance).
  • Collisions:
    • Elastic: Momentum + KE conserved.
    • Inelastic: Momentum conserved, KE not conserved.
    • Perfectly inelastic: Bodies stick, max KE lost.
  • Applications: Hydroelectric plants, automobiles, satellites, sports, machines, appliances.

All Class NCERT Solutions

PA1 Sample Papers

NEET Preparation Resources

Class-Wise NCERT Solutions

Class 8

Class 9

Class 10

Oxford Science Solutions (Classes 6 to 8)

Periodic Assessment 1 (PA1) Class Test – Questions & Answers

Class 11 NCERT Solutions

Class 12 NCERT Solutions

Class 10 Sample Papers with Answers (2018–2025)

NEET Biology MCQs – Solved Previous Year Questions

NCERT Resource Hub

Math & Science Solutions by Class

Class 10

Class 9

Class 8

Class 7

Class 6

Class 12

Class 11

Learn more about circle formulas from NCERT.

Class-wise Solutions

Class 12:

Class 12 Physics – NCERT Solutions

Class 12 Chemistry – NCERT Solutions

Class 11:

Class 10:

Class 9:

Class 8:

Class 7:

Class 6:

Subject-wise Solutions

Physics:

Chemistry:

Biology:

Math:

Science:

NEET BIOLOGY