NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2 focuses on the relationship between the zeroes and the coefficients of a polynomial. This is an important concept that helps students understand how the roots of a quadratic polynomial are connected to the numbers in the expression. The questions in this exercise require you to find the zeroes of a given quadratic polynomial and then verify the relationship using formulas.
NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2 Solutions
Question 1
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and their coefficients:
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u
(v) t2 – 15
(vi) 3x2 – x – 4
Solution:
(i) x² – 2x – 8
Factorizing:
x² – 2x – 8 = (x – 4)(x + 2)
So, zeroes are x = 4 and x = –2
Sum of zeroes = 4 + (–2) = 2
Product of zeroes = 4 × (–2) = –8
Now, from the polynomial:
a = 1, b = –2, c = –8
–b/a = –(–2)/1 = 2
c/a = –8/1 = –8
Verified
(ii) 4s² – 4s + 1
Factorizing:
4s² – 4s + 1 = (2s – 1)²
Zeroes are s = 1/2 and s = 1/2
Sum = 1/2 + 1/2 = 1
Product = (1/2) × (1/2) = 1/4
Now, a = 4, b = –4, c = 1
–b/a = –(–4)/4 = 1
c/a = 1/4
Verified
(iii) 6x² – 3 – 7x
Rewriting:
6x² – 7x – 3
Factorizing:
6x² – 9x + 2x – 3 = 3x(2x – 3) + 1(2x – 3)
= (3x + 1)(2x – 3)
Zeroes are x = –1/3 and x = 3/2
Sum = –1/3 + 3/2 = (–2 + 9)/6 = 7/6
Product = (–1/3) × (3/2) = –1/2
Now, a = 6, b = –7, c = –3
–b/a = 7/6
c/a = –3/6 = –1/2
Verified
(iv) 4u² + 8u
Taking common factor:
= 4u(u + 2)
Zeroes are u = 0 and u = –2
Sum = 0 + (–2) = –2
Product = 0 × (–2) = 0
Now, a = 4, b = 8, c = 0
–b/a = –8/4 = –2
c/a = 0/4 = 0
Verified
(v) t² – 15
= t² – 0t – 15
Factorizing:
= (t – √15)(t + √15)
Zeroes: t = √15 and t = –√15
Sum = √15 + (–√15) = 0
Product = √15 × (–√15) = –15
Now, a = 1, b = 0, c = –15
–b/a = 0
c/a = –15
Verified
(vi) 3x² – x – 4
Factorizing:
3x² – 4x + 3x – 4 = x(3x – 4) + 1(3x – 4)
= (x + 1)(3x – 4)
Zeroes: x = –1 and x = 4/3
Sum = –1 + 4/3 = (–3 + 4)/3 = 1/3
Product = –1 × 4/3 = –4/3
Now, a = 3, b = –1, c = –4
–b/a = 1/3
c/a = –4/3
Verified
Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively: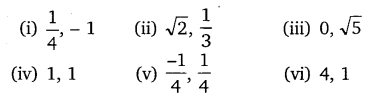
Solution:
If α and β are the zeroes (roots), and:
- Sum of roots = α + β = S
- Product of roots = α·β = P
Then the quadratic polynomial is:
x2–(Sum of roots)⋅x+(Product of roots)
(i) Sum = 1/4, Product = –1
Polynomial:
x² – (1/4)x – 1
(ii) Sum = √2, Product = 1/3
Polynomial:
x² – √2·x + 1/3
(iii) Sum = 0, Product = √5
Polynomial:
x² + √5
(Note: since sum = 0, middle term is missing)
(iv) Sum = 1, Product = 1
Polynomial:
x² – x + 1
(v) Sum = –1/4, Product = 1/4
Polynomial:
x² + (1/4)x + 1/4
(Note: –(–1/4) = +1/4)
(vi) Sum = 4, Product = 1
Polynomial:
x² – 4x + 1
New Syllabus – NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2
Question 1:
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x^2 – 2x – 8
Solution: Factorizing,
x^2 – 2x – 8 = (x – 4)(x + 2)
Zeroes are 4 and -2
Sum of zeroes = 4 + (-2) = 2
Product of zeroes = 4 * (-2) = -8
Compare with -b/a = 2 and c/a = -8
Verified
(ii) 4s^2 – 4s + 1
Solution: 4s^2 – 4s + 1 = (2s – 1)^2
Zeroes are 1/2 and 1/2
Sum = 1/2 + 1/2 = 1
Product = 1/2 * 1/2 = 1/4
Compare with -b/a = 1 and c/a = 1/4
Verified
(iii) 6x^2 – 3 – 7x
Rewriting: 6x^2 – 7x – 3
Factorizing: (3x + 1)(2x – 3)
Zeroes are -1/3 and 3/2
Sum = -1/3 + 3/2 = 7/6
Product = -1/3 * 3/2 = -1/2
Compare with -b/a = 7/6 and c/a = -1/2
Verified
(iv) 4u^2 + 8u
Solution: 4u(u + 2)
Zeroes are 0 and -2
Sum = 0 + (-2) = -2
Product = 0 * (-2) = 0
Compare with -b/a = -2 and c/a = 0
Verified
(v) t^2 – 15
Solution: t^2 – 15 = (t – √15)(t + √15)
Zeroes are √15 and -√15
Sum = √15 + (-√15) = 0
Product = √15 * (-√15) = -15
Compare with -b/a = 0 and c/a = -15
Verified
(vi) 3x^2 – x – 4
Use quadratic formula:
Discriminant D = (-1)^2 – 43(-4) = 1 + 48 = 49
x = (1 ± √49) / (2*3)
x = (1 + 7)/6 = 4/3 and (1 – 7)/6 = -1
Zeroes are 4/3 and -1
Sum = 4/3 + (-1) = 1/3
Product = 4/3 * (-1) = -4/3
Compare with -b/a = 1/3 and c/a = -4/3
Verified
Question 2:
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes.
(i) Sum = -1/4, Product = 1
Polynomial: x^2 + (1/4)x + 1
(ii) Sum = 1/2, Product = 1/3
Polynomial: x^2 – (1/2)x + 1/3
(iii) Sum = 0, Product = 5
Polynomial: x^2 + 5
(iv) Sum = 1, Product = 1
Polynomial: x^2 – x + 1
(v) Sum = -1/4, Product = 1/4
Polynomial: x^2 + (1/4)x + 1/4
(vi) Sum = 4, Product = 1
Polynomial: x^2 – 4x + 1
Polynomial: x^2 – 4x + 1
Extra Questions on Quadratic Polynomials using Sum and Product of Zeroes
Q1. Find the quadratic polynomial whose zeroes have the following:
(a) Sum = 3, Product = 2
(b) Sum = –2, Product = –8
(c) Sum = 5/2, Product = –3
(d) Sum = √3, Product = 1
(e) Sum = –√7, Product = 4
Q2. Form quadratic polynomials from the following conditions:
(a) One root is double the other, and their sum is 6
(b) One root is half the other, and their product is 8
(c) Roots are equal and their sum is –6
(d) Roots differ by 2 and their product is 15
(e) The sum of roots is zero and product is a negative number
Q3. Given the following roots, find the quadratic polynomial:
(a) Roots: 2 and 5
(b) Roots: –1/2 and 3
(c) Roots: –√2 and √2
(d) Roots: 4/3 and –2/3
(e) Roots: 1/5 and 1/5
Q4. True or False. Justify your answer.
(a) If the sum of zeroes is 0, then the polynomial has no x-term.
(b) If the product of zeroes is negative, the roots are always real.
(c) Every quadratic polynomial has two real zeroes.
(d) A quadratic polynomial with equal roots has its discriminant equal to zero.
(e) If one root is irrational, the other root must be irrational too.
Q5. Fill in the blanks:
(a) The general form of a quadratic polynomial with sum S and product P is _______.
(b) If the roots are 3 and –3, then the polynomial is _______.
(c) If the roots are imaginary, the discriminant must be _______.
(d) If both roots are the same, then the polynomial is a _______ square.
(e) If sum = 7 and product = 10, the quadratic polynomial is _______.
You can access the official NCERT Solutions for Class 10 Mathematics on the NCERT website at the following link:
NCERT Class 10 Mathematics Solutions
This page will guide you to the textbook and solutions, as provided by the National Council of Educational Research and Training (NCERT).
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
By solving NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2, students gain a strong understanding of quadratic equations and how to determine their roots using factorization. Practicing from NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2 helps build confidence in identifying the nature of roots and forming equations from given conditions.
These NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2 are designed to strengthen your conceptual clarity and problem-solving approach. Whether you’re revising or preparing for exams, NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2 serve as a reliable guide. Make sure to regularly practice NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2 to boost your accuracy and performance in exams.
