Carnot Engine Working and Efficiency

The Carnot Engine Working and Efficiency is an ideal heat engine proposed by Sadi Carnot (1824). It is a theoretical engine that operates between two heat reservoirs and converts heat into work with maximum possible efficiency. No real engine can be more efficient than a Carnot engine working between the same two temperatures.

The Carnot engine helps us understand the upper limit of efficiency of all heat engines and forms the foundation of the second law of thermodynamics.

Carnot Engine Working and Efficiency

Basic Components of a Carnot Engine

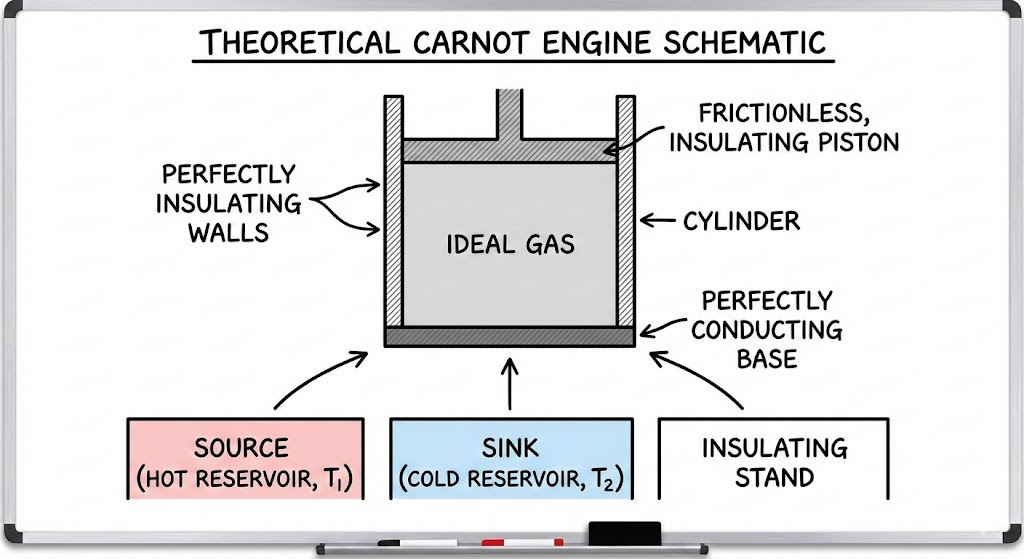
Construction of Carnot Engine

The main parts of a Carnot engine are:

• A cylinder with perfectly insulating walls
• A frictionless piston fitted inside the cylinder
• An ideal gas as the working substance
• A hot reservoir maintained at a constant temperature $T_1$T1​
• A cold reservoir maintained at a constant temperature $T_2$T2​

The piston can move freely without friction, and the cylinder can be brought into contact with either the hot reservoir or the cold reservoir as required during the cycle, which consists of four steps in Carnot Engine Working and Efficiency

Carnot Cycle (Four Reversible Processes)

The Carnot cycle has two isothermal processes and two adiabatic processes.

1. Isothermal Expansion (A → B)

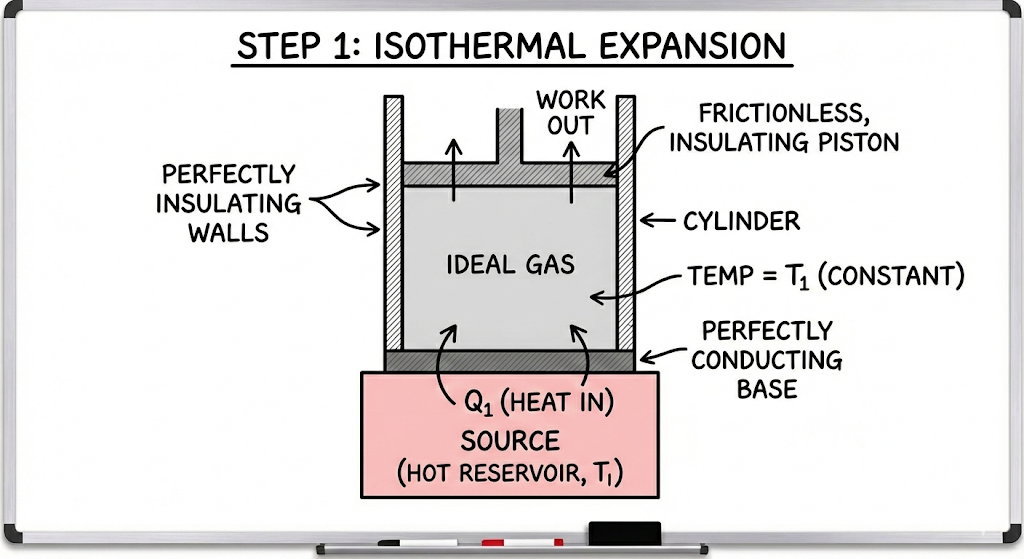
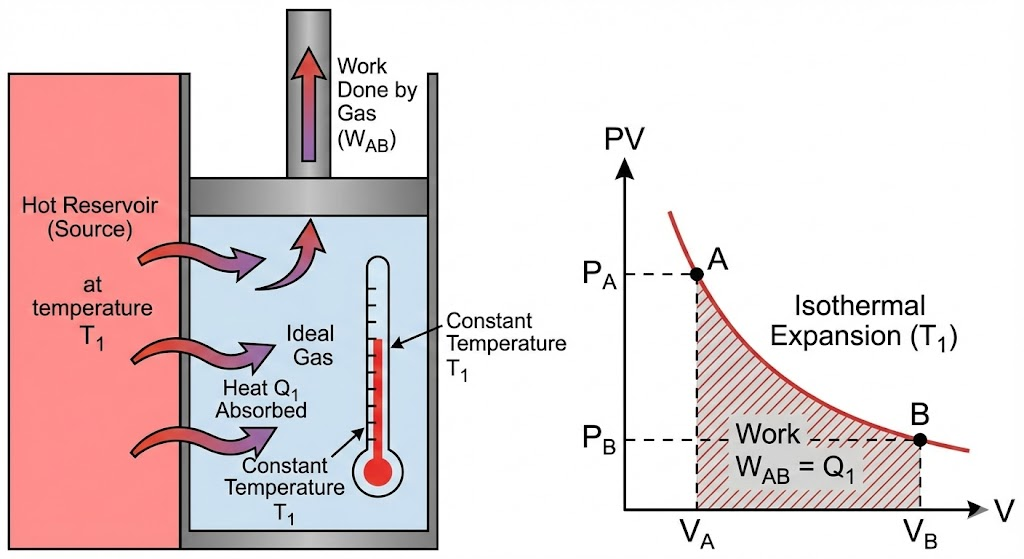
• The working gas is in contact with the hot reservoir at temperature T₁
• The gas absorbs heat Q₁ from the source
• Temperature remains constant
• The gas expands slowly
• Work is done by the gas

Since temperature is constant, all the absorbed heat is converted into work.

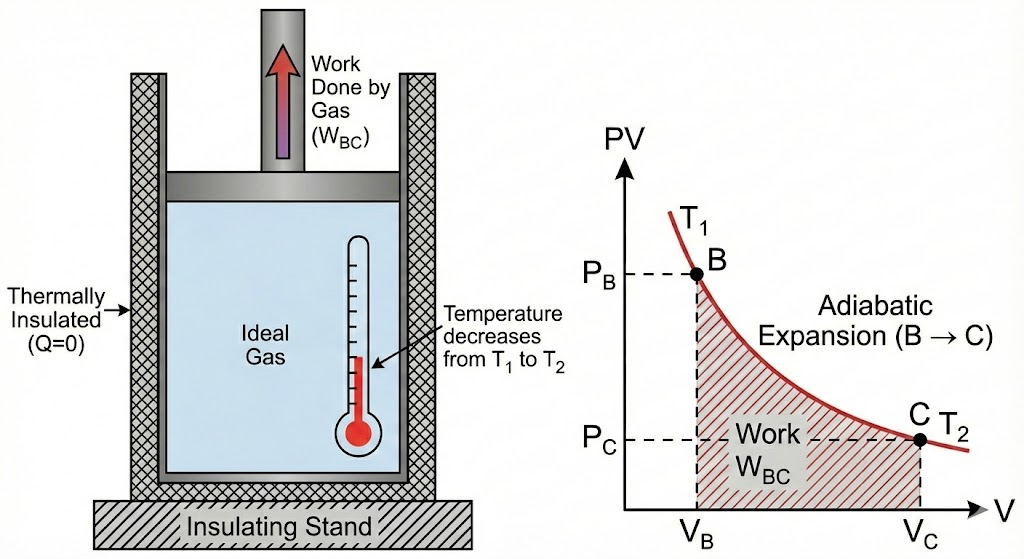
2. Adiabatic Expansion (B → C)

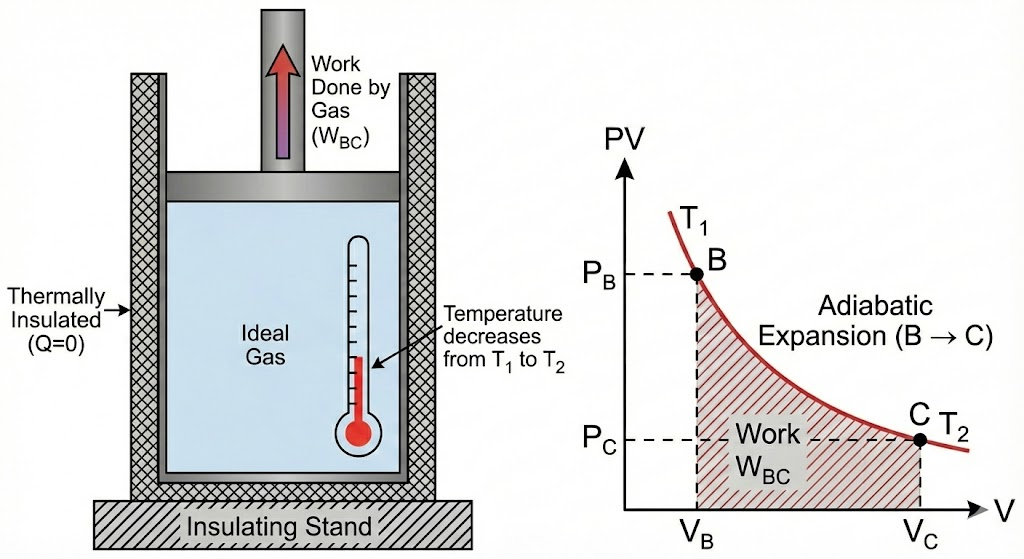
• The system is thermally insulated
• No heat exchange takes place (Q = 0)
• The gas continues to expand
• Temperature falls from T₁ to T₂
• Work is done by the gas at the expense of internal energy

3. Isothermal Compression (C → D)

• The gas is placed in contact with the cold reservoir at temperature T₂
• The gas rejects heat Q₂ to the sink
• Temperature remains constant
• External work is done on the gas
• Volume decreases

4. Adiabatic Compression (D → A)

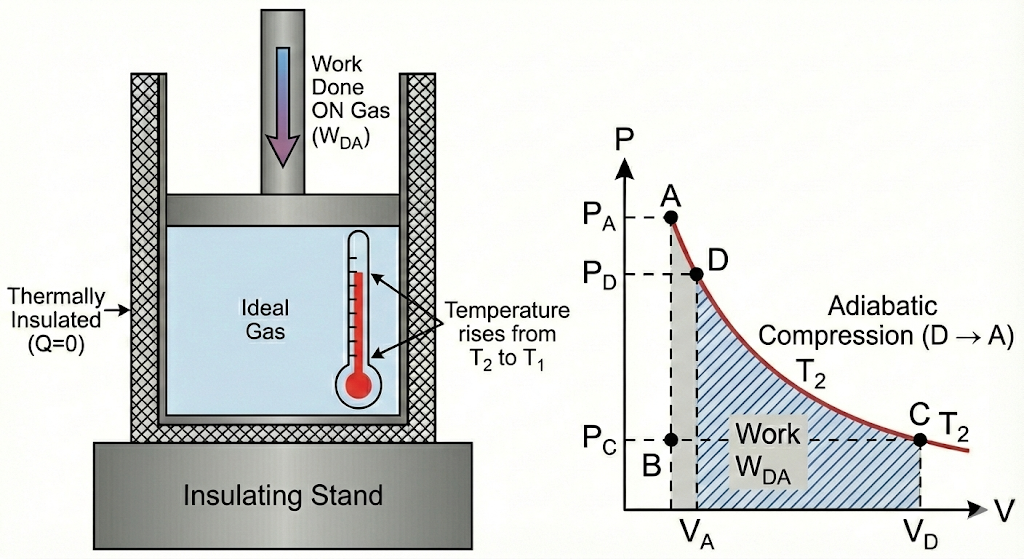
• The system is again thermally insulated
• No heat exchange occurs
• Gas is compressed
• Temperature rises from T₂ back to T₁
• The system returns to its initial state

This completes one Carnot cycle.

If not understood then again see

1. Isothermal Expansion

In the first step, the cylinder containing the ideal gas is placed in contact with a high-temperature heat source (TH​). The gas absorbs heat (QH​) and expands, pushing the piston outwards. This process happens slowly enough that the temperature of the gas remains constant at TH​.

2. Adiabatic Expansion

Next, the cylinder is placed on an insulating stand, preventing any heat from entering or leaving. The gas continues to expand and do work on the piston. Since no heat is added, the energy for this work comes from the gas’s internal energy, causing its temperature to drop from TH​ to a lower temperature, TC​.

3. Isothermal Compression

In the third step, the cylinder is placed in contact with a cold heat sink (TC​). An external force pushes the piston inwards, compressing the gas. The heat generated by this compression (QC​) is rejected into the cold sink, keeping the gas temperature constant at TC​.

4. Adiabatic Compression

Finally, the cylinder is placed back on the insulating stand. The piston continues to compress the gas. Since the system is insulated, the work done on the gas increases its internal energy, causing its temperature to rise from TC​ back to the initial high temperature, TH​. The cycle is now complete.

Diagram of Carnot Engine (P–V Diagram)

You should draw this diagram in exams:

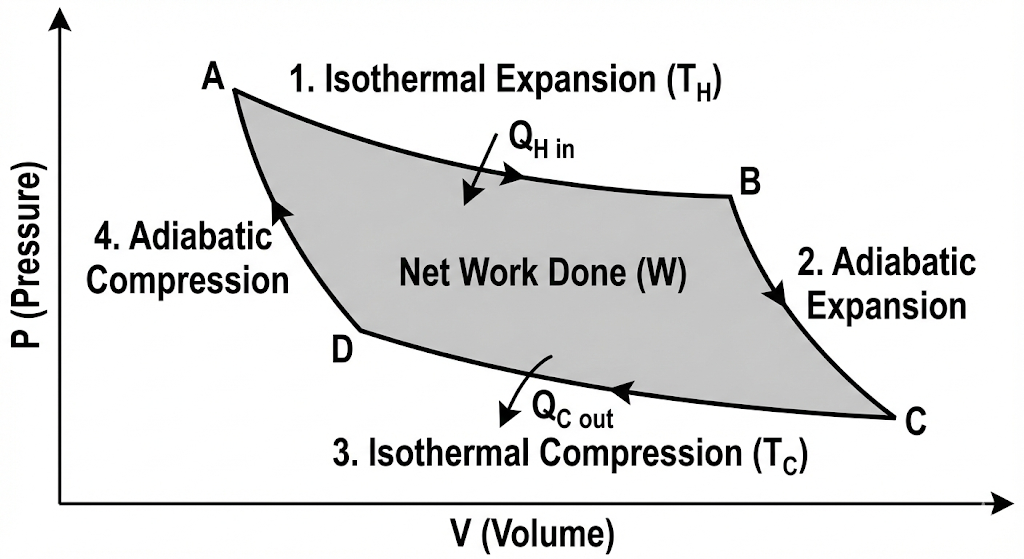
• The upper curve (AB) is an isothermal curve at T₁
• The lower curve (CD) is an isothermal curve at T₂
• The two side curves are adiabatic curves
• The area enclosed represents the work done per cycle

Carnot Engine Working and Efficiency

Efficiency (η) of a heat engine is defined as:

η = (Work done) / (Heat absorbed)

For a Carnot engine:

η = 1 − (Q₂ / Q₁)

For reversible processes:

Q₁ / T₁ = Q₂ / T₂

So,

η = 1 − (T₂ / T₁)

Where:

• T₁ = temperature of hot reservoir (in Kelvin)
• T₂ = temperature of cold reservoir (in Kelvin)

Important Features of Carnot Engine Working and Efficiency

1. Maximum efficiency
   No engine operating between the same two temperatures can be more efficient.
2. Depends only on temperatures
   Efficiency does not depend on:
   • Nature of working substance
   • Design of the engine
3. Ideal and reversible
   All processes are reversible, which is not possible in real engines.
4. Impossible in practice
   Perfect insulation and infinitely slow processes are not achievable.

Why Carnot Engine Is Not Practically Possible

• Heat transfer without temperature difference is impossible
• Perfect thermal insulation does not exist
• Frictionless pistons cannot be made
• All real processes are irreversible

Therefore, the Carnot engine is a theoretical model, not a real machine.

Significance of Carnot Engine Working and Efficiency

1. Sets the upper limit of efficiency of heat engines
2. Forms the basis of the second law of thermodynamics
3. Helps compare real engines
4. Introduces the concept of absolute temperature scale

Mathematical Derivation of Carnot Engine Working and Efficiency

(Using Work Done in Each Process)

Given

• T₁ = temperature of hot reservoir (Kelvin)
• T₂ = temperature of cold reservoir (Kelvin)
• P, V = pressure and volume of the gas
• Working substance = ideal gas
• Carnot cycle consists of four reversible processes

Step 1: Work Done in Each Process

(i) Isothermal Expansion (A → B) at Temperature T₁

For isothermal process of an ideal gas:$$W_{AB} = nRT_1 \ln\left(\frac{V_B}{V_A}\right)$$

Heat absorbed from the source:$$Q_1 = W_{AB} = nRT_1 \ln\left(\frac{V_B}{V_A}\right)$$

(because ΔU = 0 for isothermal process)

(ii) Adiabatic Expansion (B → C)

For an adiabatic process:$$PV^\gamma = \text{constant}$$

Work done:$$W_{BC} = \frac{P_BV_B – P_CV_C}{\gamma – 1}$$

Also,$$T_1 V_B^{\gamma-1} = T_2 V_C^{\gamma-1}$$…… (1)

(iii) Isothermal Compression (C → D) at Temperature T₂

Work done on the gas:$$W_{CD} = nRT_2 \ln\left(\frac{V_D}{V_C}\right)$$

Heat rejected to the sink:$$Q_2 = nRT_2 \ln\left(\frac{V_C}{V_D}\right)$$

(iv) Adiabatic Compression (D → A)

Work done on the gas:$$W_{DA} = \frac{P_DV_D – P_AV_A}{\gamma – 1}$$

For this adiabatic process:$$T_2 V_D^{\gamma-1} = T_1 V_A^{\gamma-1}$$

…… (2)

Step 2: Net Work Done in One Cycle

Total work done:$$W = W_{AB} + W_{BC} + W_{CD} + W_{DA}$$

For a complete Carnot cycle:$$W = Q_1 – Q_2$$

Substituting Q₁ and Q₂:$$W = nRT_1 \ln\left(\frac{V_B}{V_A}\right) – nRT_2 \ln\left(\frac{V_C}{V_D}\right)$$

…… (3)

Step 3: Relation Between Volumes

From equations (1) and (2):$$\frac{V_B}{V_A} = \frac{V_C}{V_D}$$

Therefore:$$\ln\left(\frac{V_B}{V_A}\right) = \ln\left(\frac{V_C}{V_D}\right)$$

…… (4)

Step 4: Substitute Volume Relation in Work Expression

Using (4) in (3):$$W = nR (T_1 – T_2) \ln\left(\frac{V_B}{V_A}\right)$$

Step 5: Efficiency of Carnot Engine

Efficiency:$$\eta = \frac{W}{Q_1}$$

Substitute values:$$\eta = \frac{nR (T_1 – T_2) \ln\left(\frac{V_B}{V_A}\right)} {nRT_1 \ln\left(\frac{V_B}{V_A}\right)}$$

Cancel common terms:$$\boxed{\eta = 1 – \frac{T_2}{T_1}}$$

Key Examiner Notes (VERY Important)

• Temperatures must be in Kelvin for Carnot Engine Working and Efficiency
• Carnot Engine Working and Efficiency depends only on reservoir temperatures
• Independent of:
  • Working substance
  • Volume, pressure, or gas type
• Carnot engine gives maximum possible efficiency

Conclusion (Write This)

Thus, by calculating the work done in each process of the Carnot cycle and using thermodynamic relations, the efficiency of a Carnot engine is obtained as$$\eta = 1 – \frac{T_2}{T_1}$$

which is the maximum efficiency attainable by any heat engine operating between the same two temperatures.

Clear more concept :

Key Aspects of Isothermal Expansion: 

• Constant Temperature: The system remains in thermal equilibrium with its surroundings, ensuring $T$ is constant.
• Internal Energy: Because internal energy for an ideal gas depends solely on temperature, $\Delta U=0$
• First Law of Thermodynamics: The heat supplied (𝑞) to the system is entirely converted into work (𝑤) done by the system (q=−𝑤, with $w$ being negative in some conventions, indicating work done by the system).
• Work Done Formula: For a reversible process, the work done $W$ during expansion from volume 𝑉1 to 𝑉2 is: $W=nRT\ln \left(\frac{V_2}{V_1}\right)$𝑊=𝑛𝑅𝑇ln𝑉2/𝑉1
  where 𝑛 is moles, 𝑅 is the gas constant, and 𝑇 is temperature.
• Pressure-Volume Relationship: Following Boyle’s Law (pv=constant), as volume increases, pressure decreases. 

Comparison with Adiabatic Expansion:
Unlike adiabatic expansion, where no heat is exchanged (𝑞=0) and temperature drops, isothermal expansion requires a constant, controlled heat exchange with the surroundings to keep the temperature from dropping. 

Conclusion

The Carnot engine is an ideal heat engine that operates between two heat reservoirs through four reversible processes—two isothermal and two adiabatic. Although it cannot be constructed practically, it plays a crucial role in thermodynamics by defining the maximum possible efficiency of any heat engine. Its efficiency depends only on the temperatures of the source and sink, making it a fundamental benchmark for all real engines.

For the official Class 11 Physics Solutions, you can visit:

1. NCERT Textbooks

ncert resources

Class-wise Solutions

Class 12:

Class 12 Physics – NCERT Solutions

Class 12 Chemistry – NCERT Solutions

Class 11:

• Class 11 Physics – NCERT Solutions
• Class 11 Chemistry – NCERT Solutions
• Class 11 Biology – NCERT Solutions
• Class 11 Math – NCERT Solutions

Class 10:

• Class 10 Science – NCERT Solutions
• Class 10 Math – NCERT Solutions
• Class 10 Science – CBSE SQP 2024

Class 9:

• Class 9 Science – NCERT Solutions
• Class 9 Math – NCERT Solutions

Class 8:

• Class 8 Science – Oxford Solutions
• Class 8 Science – NCERT Solutions

Class 7:

• Class 7 Science – Oxford Solutions

Class 6:

• Class 6 Science – Oxford Solutions