Kinetic Theory of gases Grade 11 NCERT,CBSE

🌬️ Introduction to Kinetic Theory of gases Grade 11 NCERT

In previous chapters, we studied the macroscopic properties of gases—like pressure, volume, and temperature—using the Ideal Gas Laws. However, these laws don’t explain why a gas behaves the way it does.

The Kinetic Theory of gases Grade 11 NCERT (KTG) provides the answer by looking at the microscopic level. It treats a gas not as a continuous fluid, but as a collection of billions of tiny, rapidly moving molecules. By analyzing the mechanics of these particles, we can derive fundamental properties and understand the true meaning of Temperature as a measure of molecular kinetic energy.

Example questions

Example 12.1 The density of water is 1000 kg m–3. The density of water vapour at 100 °C and 1 atm pressure is 0.6 kg m–3. The volume of a molecule multiplied by the total number gives ,what is called, molecular volume. Estimate the ratio (or fraction) of the molecular volume to the total volume occupied by the water vapour under the above conditions of temperature and pressure.

Solution: Let us take 1 kg of water.

Volume of 1 kg water in liquid state
V(liquid) = mass / density
V(liquid) = 1 / 1000
V(liquid) = 0.001 m³

This represents the actual volume occupied by the molecules (molecular volume).

Now, volume of 1 kg water in vapour state
V(vapour) = mass / density
V(vapour) = 1 / 0.6
V(vapour) = 1.67 m³

Required ratio = Molecular volume / Total volume of vapour

Ratio = 0.001 / 1.67

Ratio ≈ 6 × 10⁻⁴

Example 12.2 Estimate the volume of a water molecule using the data in Example 12.1.

Solution: Given:
Density of water = 1000 kg m⁻³
Molar mass of water = 18 g mol⁻¹ = 18 × 10⁻³ kg mol⁻¹
Avogadro number, Nₐ = 6.02 × 10²³ mol⁻¹

Solution:

Volume of 1 kg of water

V = mass / density
V = 1 / 1000
V = 0.001 m³

Number of moles in 1 kg water

n = mass / molar mass
n = 1 / (18 × 10⁻³)
n ≈ 55.6 mol

Number of molecules in 1 kg water

N = n × Nₐ
N = 55.6 × (6.02 × 10²³)
N ≈ 3.35 × 10²⁵ molecules

Volume of one molecule

Volume per molecule = Total volume / Total number of molecules

V₁ = 0.001 / (3.35 × 10²⁵)

V₁ ≈ 3 × 10⁻²⁹ m³

Example 12.3 What is the average distance between atoms (interatomic distance) in water? Use the data given in Examples 12.1 and 12.2.

Solution:

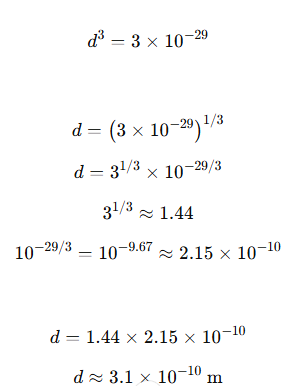
Example 12.4 A vessel contains two nonreactive gases : neon (monatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of

(i) number of molecules and (ii) mass density of neon and oxygen in the vessel.

Atomic mass of Ne = 20.2 u, molecular mass of O2 = 32.0 u.

Solution: Given:
Neon (Ne) → monatomic gas
Oxygen (O₂) → diatomic gas

Ratio of partial pressures:$$P_{Ne} : P_{O_2} = 3 : 2$$

Atomic mass of Ne = 20.2 u
Molecular mass of O₂ = 32 u

(i) Ratio of number of molecules

From ideal gas law:$$P = \frac{nRT}{V}$$

At same temperature and same volume,$$P \propto n$$

So,$$\frac{n_{Ne}}{n_{O_2}} = \frac{P_{Ne}}{P_{O_2}}$$$$\frac{n_{Ne}}{n_{O_2}} = \frac{3}{2}$$$$\boxed{n_{Ne} : n_{O_2} = 3 : 2}$$

(ii) Ratio of mass density

Mass density:$$\rho = \frac{\text{mass}}{\text{volume}}$$ρ=volumemass​

Mass = number of molecules × mass of one molecule

So,$$\rho \propto n \times m$$

Therefore,$$\frac{\rho_{Ne}}{\rho_{O_2}} = \frac{n_{Ne} \times m_{Ne}}{n_{O_2} \times m_{O_2}}$$

Substitute values:$$= \frac{3 \times 20.2}{2 \times 32}$$$$= \frac{60.6}{64}$$$$= 0.95$$

So,$$\boxed{\rho_{Ne} : \rho_{O_2} \approx 0.95 : 1}$$

Final Answers:

(i) Number of molecules ratio$$3 : 2$$

(ii) Mass density ratio$$0.95 : 1$$

This means densities are nearly equal, but oxygen is slightly denser.

Example 12.5 A flask contains argon and chlorine in the ratio of 2:1 by mass. The temperature of the mixture is 27 °C. Obtain the ratio of

(i) average kinetic energy per molecule, and

(ii) root mean square speed vrms
of the molecules of the two gases. Atomic mass of argon = 39.9 u; Molecular mass of chlorine = 70.9 u.

Solution: Given:
Mass ratio (Ar : Cl₂) = 2 : 1
Temperature = 27°C = 300 K

Atomic mass of Ar = 39.9 u
Molecular mass of Cl₂ = 70.9 u

(i) Ratio of average kinetic energy per molecule

Average kinetic energy of a gas molecule is:$$E = \frac{3}{2} kT$$

This depends only on temperature, not on mass.

Since both gases are at the same temperature (300 K),$$E_{Ar} = E_{Cl_2}$$$$\boxed{E_{Ar} : E_{Cl_2} = 1 : 1}$$

(ii) Ratio of root mean square speed $v_{rms}$vrms​

Formula:$$v_{rms} = \sqrt{\frac{3kT}{m}}$$

So,$$v_{rms} \propto \frac{1}{\sqrt{m}}$$

Therefore,$$\frac{v_{Ar}}{v_{Cl_2}} = \sqrt{\frac{m_{Cl_2}}{m_{Ar}}}$$

Substitute values:$$= \sqrt{\frac{70.9}{39.9}}$$$$\boxed{v_{Ar} : v_{Cl_2} \approx 1.33 : 1}$$

Final Answers:

(i) Average kinetic energy ratio$$1 : 1$$

(ii) RMS speed ratio$$1.33 : 1$$

So, argon molecules move faster than chlorine molecules because argon has smaller mass.

Example 12.6 Uranium has two isotopes of masses 235 and 238 units. If both are present in Uranium hexafluoride gas which would have the larger average speed ? If atomic mass of fluorine is 19 units,
estimate the percentage difference in speeds at any temperature.

Solution: Uranium has two isotopes:
$^{235}U$235U and $^{238}U$238U

They form uranium hexafluoride gas: UF₆

Atomic mass of fluorine = 19 u

Step 1: Find molecular masses of the two gases

For $^{235}UF_6$​:$$M_1 = 235 + 6(19)$$$$M_1 = 235 + 114 = 349 \, u$$$$M_2 = 238 + 6(19)$$$$M_2 = 238 + 114 = 352 \, u$$

Step 2: Which has larger average speed?

We know,$$v_{rms} \propto \frac{1}{\sqrt{M}}$$

$$^{235}UF_6$$

has smaller mass, so it will have larger average speed.

Step 3: Percentage difference in speeds

$$\frac{v_1}{v_2} = \sqrt{\frac{M_2}{M_1}} = \sqrt{\frac{352}{349}}$$$$\frac{352}{349} \approx 1.0086$$$$\sqrt{1.0086} \approx 1.0043$$

So,$$\frac{v_1 – v_2}{v_2} = 0.0043$$

Percentage difference:$$0.0043 \times 100$$$$\approx 0.43\%$$

Final Answers

1. $^{235}UF_6$235UF6​ has the larger average speed.
2. Percentage difference in speeds ≈

$$\boxed{0.4\%}$$

So the speed difference is very small, less than 1%.

Example 12.7

(a) When a molecule (or an elastic ball) hits a ( massive) wall, it rebounds with the same speed. When a ball hits a massive bat held firmly, the same thing happens. However, when the bat is moving towards the ball, the ball rebounds with a different speed. Does the ball move faster or slower? (Ch.5 will refresh your memory on elastic collisions.)
(b) When gas in a cylinder is compressed by pushing in a piston, its temperature rises. Guess at an explanation of this in terms of kinetic theory using (a) above.

(c) What happens when a compressed gas
pushes a piston out and expands. What would you observe ?
(d) Sachin Tendulkar used a heavy cricket bat while playing. Did it help him in anyway ?

Solution: (a)

If the wall or bat is at rest and very massive, the ball rebounds with the same speed (only direction changes).

But if the bat is moving towards the ball, the ball rebounds with greater speed.

Reason:
In an elastic collision, if the massive object moves toward the ball, it transfers extra momentum and energy to the ball. So after collision, the ball moves faster than before.

✔ Answer: The ball moves faster.

(b)

When a gas is compressed by pushing a piston inward, the piston is moving towards the gas molecules.

From part (a), when a moving wall hits particles, they rebound with greater speed.

So during compression:

• Molecules collide with the inward-moving piston.
• They rebound with higher speeds.
• Their kinetic energy increases.
• Since temperature ∝ average kinetic energy,

✔ Temperature rises.

(c)

When a compressed gas expands, it pushes the piston outward.

Now the piston moves away from the molecules.

When molecules hit a retreating piston, they rebound with less speed.

So:

• Molecular kinetic energy decreases.
• Temperature decreases.

✔ You would observe cooling of the gas.

(This is the principle used in refrigerators and expansion cooling.)

(d)

Yes, it helped him.

A heavier bat has:

• Larger mass
• Smaller recoil during impact
• More momentum transfer to the ball

When the bat is massive compared to the ball, it behaves almost like a “massive wall”, so more energy is transferred to the ball.

✔ So a heavier bat can hit the ball harder (if the player can swing it properly).

Example 12.9 Estimate the mean free path for a water molecule in water vapour at 373 K. Use information from Exercises 12.1 and Eq. (12.41) above.

Solution: Step 1: Formula for mean free path

From kinetic theory,$$\lambda = \frac{1}{\sqrt{2}\,\pi d^2 n}$$

where
$d$ = diameter of molecule
$n$ = number of molecules per unit volume

Step 2: Molecular diameter

From earlier results (Exercises 12.1 / previous examples),

Intermolecular distance ≈$$d \approx 3 \times 10^{-10} \text{ m}$$

Step 3: Number density of vapour

At 373 K and 1 atm,

Density of water vapour = 0.6 kg m⁻³

Mass of one water molecule:

$$m = \frac{18 \times 10^{-3}}{6.02 \times 10^{23}}$$$$m \approx 3 \times 10^{-26} \text{ kg}$$

Now,$$n = \frac{\rho}{m}$$$$n = \frac{0.6}{3 \times 10^{-26}}$$$$n \approx 2 \times 10^{25} \text{ molecules m}^{-3}$$

Step 4: Substitute in formula

$$\lambda = \frac{1}{\sqrt{2}\,\pi (3 \times 10^{-10})^2 (2 \times 10^{25})}$$

First,$$(3 \times 10^{-10})^2 = 9 \times 10^{-20}$$

Now denominator:$$\sqrt{2} \approx 1.41$$$$1.41 \times \pi \times 9 \times 2 \approx 80$$

So denominator ≈$$80 \times 10^{5}$$$$= 8 \times 10^{6}$$

Therefore,$$\lambda \approx \frac{1}{8 \times 10^{6}}$$$$\lambda \approx 1.2 \times 10^{-7} \text{ m}$$

Final Answer

$$\boxed{\lambda \approx 10^{-7} \text{ m}}$$

So, the mean free path of a water molecule in water vapour at 373 K is of the order of$$10^{-7} \text{ m}$$

which is much larger than molecular size (~10⁻¹⁰ m).

Exercise

12.1 Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3 Å.

Solution: Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP.
Diameter of oxygen molecule,$$d = 3 \, \text{Å} = 3 \times 10^{-10} \text{ m}$$

Step 1: Volume of one oxygen molecule

Treat molecule as a sphere.

Radius,$$r = \frac{d}{2} = 1.5 \times 10^{-10} \text{ m}$$

Volume of one molecule:$$V_m = \frac{4}{3}\pi r^3$$$$V_m = \frac{4}{3}\pi (1.5 \times 10^{-10})^3$$$$= \frac{4}{3}\pi (3.375 \times 10^{-30})$$$$\approx 1.4 \times 10^{-29} \text{ m}^3$$

Step 2: Number of molecules in 1 mole

$$N_A = 6.02 \times 10^{23}$$

Total molecular volume in 1 mole:$$V_{total} = N_A \times V_m$$$$= (6.02 \times 10^{23}) (1.4 \times 10^{-29})$$$$\approx 8.4 \times 10^{-6} \text{ m}^3$$

Step 3: Actual volume of 1 mole gas at STP

At STP,$$1 \text{ mole} = 22.4 \text{ L}$$

Step 4: Required fraction

$$\text{Fraction} = \frac{8.4 \times 10^{-6}}{2.24 \times 10^{-2}}$$$$\approx 3.8 \times 10^{-4}$$

Final Answer

$$\boxed{\text{Fraction} \approx 4 \times 10^{-4}}$$

So only about 0.04% of the volume of oxygen gas at STP is actually occupied by molecules.

12.2 Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP : 1 atmospheric pressure, 0 °C). Show that it is 22.4 litres.

12.3 Figure 12.8 shows plot of PV/T versus P for 1.00×10–3 kg of oxygen gas at two different temperatures.

(a) What does the dotted plot signify?
(b) Which is true: T1 Greater than T2 or T1< T2 ?
(c) What is the value of PV/T where the curves meet on the y-axis?

(d) If we obtained similar plots for 1.00×10–3 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of PV/T (for low pressure high temperature region of the plot) ? (Molecular mass of H2 = 2.02 u, of O2 = 32.0 u, R = 8.31 J mo1–1 K–1.)

12.4 An oxygen cylinder of volume 30 litre has an initial gauge pressure of 15 atm and a temperature of 27 °C. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm and its temperature drops to 17 °C. Estimate the mass of oxygen taken out of the cylinder (R = 8.31 J mol–1 K–1, molecular mass of O2 = 32 u).

12.5 An air bubble of volume 1.0 cm3 rises from the bottom of a lake 40 m deep at a temperature of 12 °C. To what volume does it grow when it reaches the surface, which is at a temperature of 35 °C ?

12.6 Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m3 at a temperature of 27 °C and 1 atm pressure. 12.7 Estimate the average thermal energy of a helium atom at (i) room temperature (27 °C), (ii) the temperature on the surface of the Sun (6000 K), (iii) the temperature of 10 million kelvin (the typical core temperature in the case of a star).

12.8 Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules ? Is the root mean square speed of molecules the same in the three cases? If not, in which case is Vrms the largest ?

12.9 At what temperature is the root mean square speed of an atom in an argon gas
cylinder equal to the rms speed of a helium gas atom at – 20 °C ? (atomic mass of Ar
= 39.9 u, of He = 4.0 u).

12.10 Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2.0 atm and temperature 17 0C. Take the radius of a nitrogen molecule to be roughly 1.0 Å. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of N2= 28.0 u).

The list of chapters is as follows:

• Units and Measurements
• Motion in a Straight Line
• Motion in a Plane
• Laws of Motion
• Work, Energy and Power
• System of Particles and Rotational Motion
• Gravitation
• Mechanical Properties of Solids
• Mechanical Properties of Fluids
• Thermal Properties of Matter
• Thermodynamics
• Kinetic Theory
• Oscillations
• Waves

Class 11 Physics NCERT Solutions-All Chapters-OLD SYLLABUS

Chapter-wise Links:

1. Chapter 1: Physical World
2. Chapter 2: Units and Measurements
3. Chapter 3: Motion in a Straight Line
4. Chapter 4: Motion in a Plane
5. Chapter 5: Laws of Motion
6. Chapter 6: Work, Energy and Power
7. Chapter 7: System of Particles and Rotational Motion
8. Chapter 8: Gravitation
9. Chapter 9: Mechanical Properties of Solids
10. Chapter 10: Mechanical Properties of Fluids
11. Chapter 11: Thermal Properties of Matter
12. Chapter 12: Thermodynamics
13. Chapter 13: Kinetic Theory
14. Chapter 14: Oscillations
15. Chapter 15: Waves

For the official Class 11 Physics Solutions, you can visit:

1. NCERT Textbooks

ncert resources