Exercise 7.2 focuses on applying the Section Formula to find coordinates of points dividing line segments in a given ratio, along with related geometric problems. Here’s a brief overview of the solutions:

Class 10 Math Ch 7 Coordinate Geometry Ex 7.2 – Textbook
Question 1.
Find the coordinates of the point which divides the join of (-1, 7) and (4, -3) in the ratio 2 : 3.
Solution: Use the section formula.
For A(x₁, y₁)=(-1, 7), B(x₂, y₂)=(4, -3) and ratio m:n = 2:3,
x = (m x₂ + n x₁) / (m+n) = (2·4 + 3·(-1)) / 5 = (8 − 3) / 5 = 1
y = (m y₂ + n y₁) / (m+n) = (2·(-3) + 3·7) / 5 = (-6 + 21) / 5 = 3
So, the coordinates are (1, 3).
Question 2.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Solution:
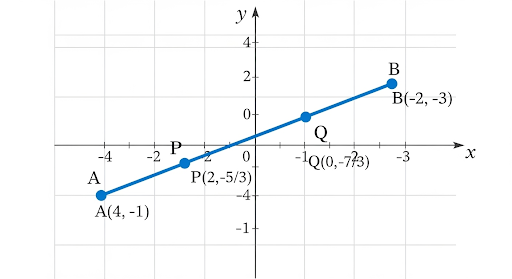
To trisect the line segment joining A(4, -1) and B(-2, -3), we need the points dividing AB in the ratio 1:2 and 2:1.
Using the section formula:
- Point dividing AB in ratio 1:2
x = (1 × -2 + 2 × 4) / 3 = ( -2 + 8 ) / 3 = 6 / 3 = 2
y = (1 × -3 + 2 × -1) / 3 = ( -3 – 2 ) / 3 = -5 / 3
So, the first point is (2, -5/3). - Point dividing AB in ratio 2:1
x = (2 × -2 + 1 × 4) / 3 = ( -4 + 4 ) / 3 = 0 / 3 = 0
y = (2 × -3 + 1 × -1) / 3 = ( -6 – 1 ) / 3 = -7 / 3
So, the second point is (0, -7/3).
Final Answer:
The points of trisection are (2, -5/3) and (0, -7/3).
Question 3.
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in given
figure below. Niharika runs 14 th the distance AD on the 2nd line and posts a green flag. Preet runs 15 th distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?
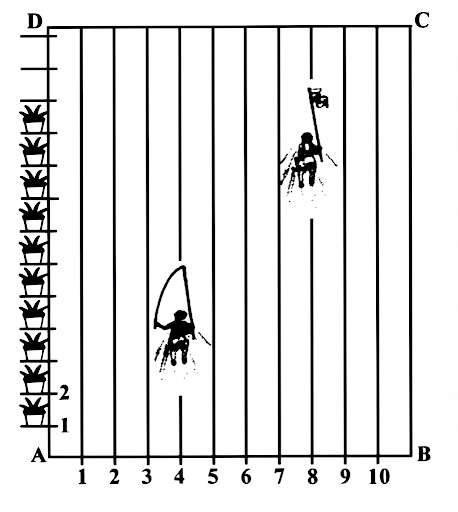
Solution:
Let A be (0, 0), AB along the x-axis and AD along the y-axis.
Since there are 100 flower pots placed 1 m apart on AD, the length of AD = 100 m.
Niharika: She runs 1/4th of AD on the 2nd line.
So, x = 2 and y = 1/4 × 100 = 25.
Green flag is at (2, 25).
Preet: He runs 1/5th of AD on the 8th line.
So, x = 8 and y = 1/5 × 100 = 20.
Red flag is at (8, 20).
Distance between the two flags:
√[(8 – 2)² + (20 – 25)²] = √(36 + 25) = √61 ≈ 7.81 m.
Midpoint of the line joining the two flags:
[(2 + 8)/2, (25 + 20)/2] = (5, 22.5).
So, Rashmi should place the blue flag on the 5th line at a height of 22.5 m from A along AD.
Final Answer:
Distance between the flags = √61 ≈ 7.81 m.
Rashmi should post the blue flag at (5, 22.5).
Question 4.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Solution:
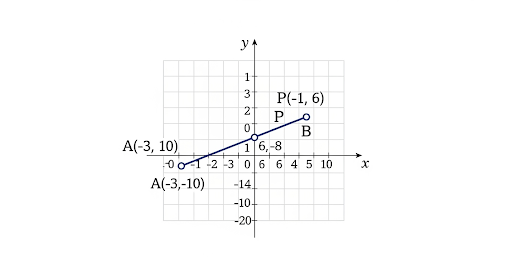
Let A = (−3, 10), B = (6, −8) and P = (−1, 6).
Suppose P divides AB in the ratio m : n.
Using section formula:
x = (m×x₂ + n×x₁) / (m + n) and y = (m×y₂ + n×y₁) / (m + n)
Substitute values for the x-coordinate:
−1 = (6m − 3n) / (m + n)
⇒ −m − n = 6m − 3n
⇒ −7m + 2n = 0
⇒ 2n = 7m
⇒ n/m = 7/2.
Now check using y-coordinate:
6 = (−8m + 10n) / (m + n)
⇒ 6m + 6n = −8m + 10n
⇒ 14m = 4n
⇒ n/m = 7/2.
Both give the same result.
So, the required ratio is 2 : 7.
Question 5.
Find the ratio in which line segment joining A (1, -5) and B (-4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
Solution:
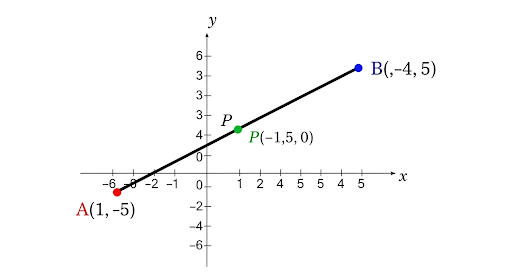
Let A = (1, −5) and B = (−4, 5).
We want the point P(x, 0) on the x-axis that divides AB.
Using section formula:
P(x, y) = (m x₂ + n x₁) / (m + n), (m y₂ + n y₁) / (m + n)
Since y = 0 (point lies on x-axis):
0 = (m·5 + n·(−5)) / (m + n)
0 = (5m − 5n) / (m + n)
⇒ 5m − 5n = 0
⇒ m = n.
So, ratio is 1 : 1 (the midpoint).
Now find coordinates:
x = (m(−4) + n(1)) / (m + n)
Since m = n, take m = n = 1.
x = (−4 + 1) / 2 = −3/2 = −1.5
y = 0 (since it lies on x-axis).
Final Answer:
The x-axis divides AB in the ratio 1 : 1, and the point of division is (−1.5, 0).
Question 6.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Solution:
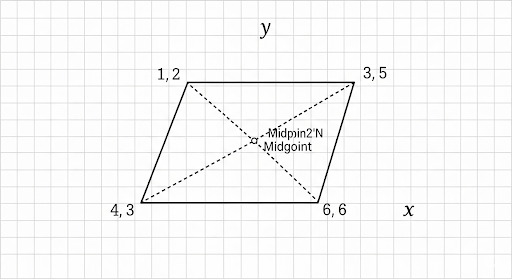
We are given four points in order: A(1, 2), B(4, y), C(x, 6), D(3, 5).
They form a parallelogram.
Property: The diagonals of a parallelogram bisect each other.
So, midpoint of AC = midpoint of BD.
Midpoint of AC = ( (1 + x)/2 , (2 + 6)/2 ) = ( (1 + x)/2 , 4 )
Midpoint of BD = ( (4 + 3)/2 , (y + 5)/2 ) = ( 7/2 , (y + 5)/2 )
Equating coordinates:
(1 + x)/2 = 7/2
⇒ 1 + x = 7
⇒ x = 6
And
4 = (y + 5)/2
⇒ y + 5 = 8
⇒ y = 3
Final Answer:
x = 6 and y = 3
Question 7.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
Solution:

We are given:
Centre of the circle O = (2, −3)
One end of diameter B = (1, 4)
We have to find the other end A.
Property: The centre of a circle is the midpoint of the diameter.
So, O is the midpoint of AB.
Using midpoint formula:
(xA + xB) / 2 = xO
(yA + yB) / 2 = yO
Substitute values:
(xA + 1) / 2 = 2
xA + 1 = 4
xA = 3
(yA + 4) / 2 = −3
yA + 4 = −6
yA = −10
Final Answer:
The coordinates of A are (3, −10).
Question 8.
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 37 AB and P lies on the line segment AB.
Solution:
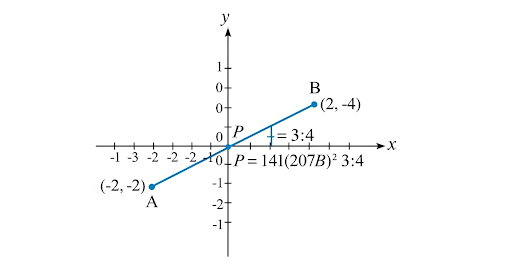
We are given A = (−2, −2) and B = (2, −4).
We want point P such that AP = 3/7 AB and P lies on AB.
This means P divides AB in the ratio 3 : 4 (because AP : PB = 3 : 4).
Using section formula for internal division:
P(x, y) = (m x₂ + n x₁) / (m + n), (m y₂ + n y₁) / (m + n)
Here, m = 3, n = 4, x₁ = −2, y₁ = −2, x₂ = 2, y₂ = −4.
x = (3 × 2 + 4 × (−2)) / (3 + 4) = (6 − 8) / 7 = −2 / 7
y = (3 × (−4) + 4 × (−2)) / (3 + 4) = (−12 − 8) / 7 = −20 / 7
Final Answer:
The coordinates of P are (−2/7, −20/7).
Question 9.
Find the coordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts.
Solution:
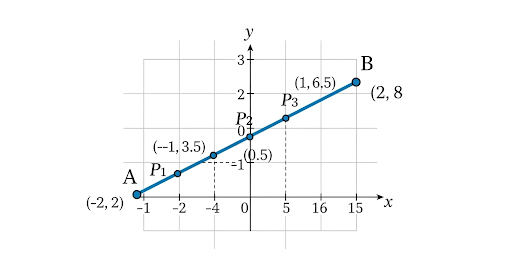
We are given A = (−2, 2) and B = (2, 8).
We want the three points that divide AB into four equal parts.
Step 1: Vector approach (or section formula repeatedly).
If a line is divided into 4 equal parts, the points are at ratios 1:4, 2:4, and 3:4.
Step 2: Using section formula.
Point P₁ divides AB in ratio 1:3.
x = (1×2 + 3×(−2)) / (1+3) = (2 − 6) / 4 = −1
y = (1×8 + 3×2) / (1+3) = (8 + 6) / 4 = 14 / 4 = 7/2
So, P₁ = (−1, 7/2).
Point P₂ divides AB in ratio 1:1 (midpoint).
x = (−2 + 2) / 2 = 0
y = (2 + 8) / 2 = 5
So, P₂ = (0, 5).
Point P₃ divides AB in ratio 3:1.
x = (3×2 + 1×(−2)) / (3+1) = (6 − 2) / 4 = 1
y = (3×8 + 1×2) / (3+1) = (24 + 2) / 4 = 26 / 4 = 13/2
So, P₃ = (1, 13/2).
Final Answer:
The three points dividing AB into four equal parts are
(−1, 7/2), (0, 5), and (1, 13/2).
Question 10.
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2, -1) taken in order.
[Hint: Area of a rhombus = 12 (product of its diagonals)]
Solution:
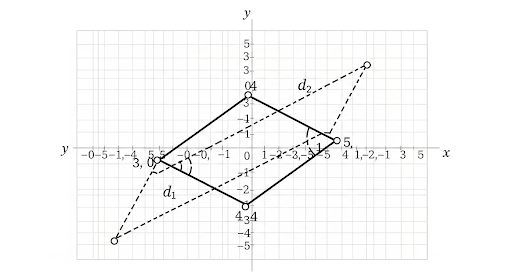
We are given vertices of the rhombus: A(3, 0), B(4, 5), C(−1, 4), D(−2, −1) in order.
Hint says: Area of rhombus = 1/2 × (product of its diagonals).
Step 1: Find the lengths of diagonals AC and BD.
Diagonal AC connects A(3, 0) and C(−1, 4).
AC = √[(−1 − 3)² + (4 − 0)²] = √[(−4)² + 4²] = √(16 + 16) = √32 = 4√2.
Diagonal BD connects B(4, 5) and D(−2, −1).
BD = √[(−2 − 4)² + (−1 − 5)²] = √[(−6)² + (−6)²] = √(36 + 36) = √72 = 6√2.
Step 2: Area = 1/2 × AC × BD
= 1/2 × (4√2 × 6√2)
= 1/2 × (24 × 2)
= 24.
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
Exercise 7.2 helps students understand and apply the Section Formula to find the coordinates of a point dividing a line segment in a given ratio. Through various problems, students learn to calculate points of trisection, midpoints, and verify line divisions using algebraic methods. This exercise strengthens spatial understanding and is useful in real-life applications like map reading and computer graphics.
The line joining two points can be divided internally in a given ratio using the section formula, which is the key concept explored in this exercise. Mastering this builds a strong foundation in coordinate geometry.
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
