Welcome to the Class 10 Math Ch 8 Trigonometry Ex 8.3Solutions page. This exercise deals with questions based on trigonometric identities, which are crucial for simplifying expressions and solving trigonometric equations.

Our step-by-step solutions are designed according to the NCERT and CBSE guidelines and help students understand the logic behind each step
Class 10 Math Ch 8 Trigonometry Ex 8.3 Textbook
Ex 8.3 Class 10 Maths Question 1.
Evaluate:![]()
Solution: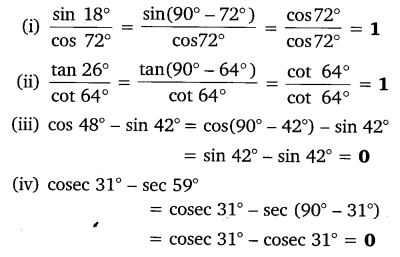
Ex 8.3 Class 10 Maths Question 2
Show that:
(i) tan 48° × tan 23° × tan 42° × tan 67° = 1
(ii) cos 38° × cos 52° – sin 38° × sin 52° = 0
Solution:
(i)
We know that:
tan θ × tan (90° – θ) = 1
Now group the terms:
tan 48° × tan 42° = tan 48° × tan (90° – 48°) = 1
tan 23° × tan 67° = tan 23° × tan (90° – 23°) = 1
So,
tan 48° × tan 23° × tan 42° × tan 67°
= (tan 48° × tan 42°) × (tan 23° × tan 67°)
= 1 × 1 = 1
Hence proved.
(ii)
We know the identity:
cos A × cos B – sin A × sin B = cos (A + B)
Apply the identity:
cos 38° × cos 52° – sin 38° × sin 52°
= cos (38° + 52°)
= cos 90° = 0
Hence proved.
Ex 8.3 Class 10 Maths Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution: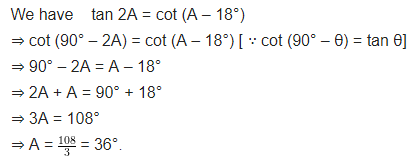
Ex 8.3 Class 10 Maths Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution:
We are given:
tan A = cot B
We know that:
cot B = tan (90° – B)
So,
tan A = tan (90° – B)
Now, if tan A = tan (90° – B), then:
⇒ A = 90° – B
⇒ A + B = 90°
Hence proved.
Ex 8.3 Class 10 Maths Question 5
Question:
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
We are given:
sec 4A = cosec (A – 20°)
We know the identity:
sec θ = cosec (90° – θ)
So,
sec 4A = cosec (90° – 4A)
Now equate it to the given RHS:
cosec (90° – 4A) = cosec (A – 20°)
⇒ Remove cosec from both sides:
90° – 4A = A – 20°
Now solve for A:
90° + 20° = A + 4A
110° = 5A
⇒ A = 22°
Ex 8.3 Class 10 Maths Question 6
Question:
If A, B and C are interior angles of a triangle ABC, then show that:
sin[(B + C)/2] = cos(A/2)
Solution:
In any triangle, we know:
A + B + C = 180°
So,
B + C = 180° – A
Now divide both sides by 2:
(B + C)/2 = (180° – A)/2 = 90° – A/2
Now take the left-hand side:
sin[(B + C)/2] = sin(90° – A/2)
We know that:
sin(90° – θ) = cos(θ)
So,
sin(90° – A/2) = cos(A/2)
Therefore,
sin[(B + C)/2] = cos(A/2)
Hence proved.
Ex 8.3 Class 10 Maths Question 7.
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:![]()
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Science Solutions, you can visit:
- NCERT Textbooks (for Class 10):
