At MathScience.in, we provide Class 10 Maths Ch 1 Real Numbers Ex 1.3 with detailed, step-by-step explanations to help students understand complex concepts easily. This exercise focuses on Euclid’s Division Lemma, which is a fundamental concept in number theory used to find the Highest Common Factor (HCF) of two numbers.

Understanding Class 10 Maths Ch 1 Real Numbers Ex 1.3 is crucial for students preparing for board exams. The concepts in this chapter build a strong mathematical foundation, which is useful in higher studies.
✔ Step-by-step explanations for better understanding
✔ Based on the latest NCERT syllabus and CBSE exam patterns
✔ Boosts problem-solving skills and conceptual clarity
✔ Free PDF download available at MathScience.in
Concepts Covered in Class 10 Maths Ch 1 Real Numbers Ex 1.3
This exercise mainly focuses on:
- Euclid’s Division Lemma: Understanding how any two positive integers can be expressed in the form a = bq + r, where 0 ≤ r < b.
- Finding HCF using Euclid’s Division Algorithm: This method helps in determining the highest common factor of two numbers efficiently.
- Application of HCF in Real-Life Problems: Learning how to apply the HCF concept in practical scenarios.
Class 10 Maths Ch 1 Real Numbers Ex 1.3 Full Chapter Answers
1.Prove that √5 is irrational.
Solution:
Assume √5 is rational.
Then it can be written as √5 = p/q,
where p and q are integers, q ≠ 0, and the fraction is in lowest terms (i.e., p and q have no common factors other than 1).
Squaring both sides:
√5 = p/q
⇒ 5 = p² / q²
⇒ 5q² = p²
This means p² is divisible by 5.
So, p is divisible by 5.
Let p = 5k, for some integer k.
Substitute p = 5k into the equation:
5q² = (5k)²
⇒ 5q² = 25k²
⇒ q² = 5k²
This means q² is divisible by 5.
So, q is also divisible by 5.
Therefore, both p and q are divisible by 5.
This contradicts the assumption that p/q is in lowest terms.
Conclusion:
Our assumption is wrong. So, √5 is irrational.
Ex 1.3 Class 10 Maths Question 2.
Show that 3 + √5 is irrational.
Solution:
Assume that 3 + √5 is rational.
Then we can write:
3 + √5 = r, where r is a rational number.
Subtract 3 from both sides:
√5 = r – 3
Since r and 3 are both rational, r – 3 is also rational.
So, √5 is rational.
But this is a contradiction, because √5 is known to be irrational.
Conclusion:
Our assumption is wrong.
Therefore, 3 + √5 is irrational.
Ex 1.3 Class 10 Maths Question 3.
Prove that the following are irrational.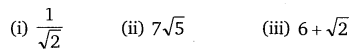
Solution:
(i) √2 is irrational
Proof (by contradiction):
- Assume √2 is rational.
- Then √2 = p/q, where p and q are integers with no common factor and q ≠ 0.
- Squaring both sides:
2 = p² / q²
⇒ 2q² = p² - So, p² is even ⇒ p is even ⇒ p = 2k
- Substitute:
p² = (2k)² = 4k²
So, 2q² = 4k² ⇒ q² = 2k² - So, q is also even ⇒ p and q have a common factor (2), contradiction.
Conclusion: √2 is irrational.
(ii) √3 is irrational
Same method:
- Assume √3 = p/q
- 3q² = p²
- p is divisible by 3 ⇒ let p = 3k
- Substitute: 3q² = 9k² ⇒ q² = 3k² ⇒ q divisible by 3
- Then both p and q are divisible by 3 ⇒ contradiction.
Conclusion: √3 is irrational.
(iii) √7 is irrational
Same steps:
- Assume √7 = p/q
- 7q² = p²
- p divisible by 7 ⇒ p = 7k
- Substitute: 7q² = 49k² ⇒ q² = 7k² ⇒ q divisible by 7
- Contradiction as p and q have a common factor.
Conclusion: √7 is irrational.
(iv) 2√5 is irrational
- √5 is irrational (already known)
- 2 × √5 is a product of a rational (2) and an irrational (√5)
- Product of a non-zero rational and an irrational number is always irrational.
Conclusion: 2√5 is irrational.
NEW SYLLABUS – Class 10 Maths Ch 1 Real Numbers Ex 1.3
Q1. Prove that √5 is irrational.
Solution:
Assume √5 is rational.
Then √5 = a/b, where a and b are integers, b ≠ 0, and a and b are coprime.
Squaring both sides:
5 = a² / b² ⇒ a² = 5b²
⇒ 5 divides a² ⇒ 5 divides a
Let a = 5k
Then, a² = 25k² ⇒ 5b² = 25k² ⇒ b² = 5k²
⇒ 5 divides b
Now both a and b are divisible by 5 ⇒ contradicts that they are coprime.
∴ Our assumption is wrong.
Hence, √5 is irrational.
Q2. Prove that 3 + 2√5 is irrational.
Solution:
Assume 3 + 2√5 is rational.
Then 3 + 2√5 = a/b, where a and b are integers, b ≠ 0
Rewriting:
2√5 = a/b − 3 ⇒ √5 = (a − 3b)/(2b)
RHS is rational ⇒ implies √5 is rational
Contradiction, because √5 is irrational
∴ 3 + 2√5 is irrational
Q3. Prove that the following are irrationals:
(i) 1/√2
Solution:
Assume 1/√2 is rational
Then √2 = 1 / (rational) ⇒ implies √2 is rational
Contradiction
∴ 1/√2 is irrational
(ii) 7√5
Solution:
Assume 7√5 is rational
Then √5 = rational / 7 ⇒ implies √5 is rational
Contradiction
∴ 7√5 is irrational
(iii) 6 + √2
Solution:
Assume 6 + √2 = rational
Then √2 = rational − 6
⇒ implies √2 is rational
Contradiction
∴ 6 + √2 is irrational
Refer to NCERT for Class 10 Maths Official Book
For additional reference and to access the official NCERT Class 10 Maths textbook, visit the NCERT website. This will help you understand the concepts covered in Class 10 Maths Ch 1 Real Numbers Ex 1.3 more effectively.
🔗 Visit NCERT Official Website: NCERT Class 10 Maths Book
This resource will provide you with the complete Class 10 Maths syllabus and ensure that you’re following the latest NCERT guidelines. Happy learning!
