Class 10 Maths Circles Ex 10.1 CBSE Ex 11.1 SEBA focuses on the basic concepts of tangents to a circle. In this exercise, students will learn how to apply the properties of tangents drawn from an external point to a circle. The questions are based on proving the lengths of tangents, identifying the number of tangents, and using geometrical reasoning to solve problems. Understanding these concepts is important for building a strong foundation in geometry and improving problem-solving skills.

Class 10 Maths Circles Ex 10.1 CBSE Ex 11.1 SEBA Textbook Solutions

Ex 10.1 Class 10 Maths Question 1.
How many tangents can a circle have?
Solution:
There can be infinitely many tangents to a circle.

Ex 10.1 Class 10 Maths Question 2.
Fill in the blanks:
(i) A tangent to a circle intersects it in ………… point(s).
(ii) A line intersecting a circle in two points is called a ………… .
(iii) A circle can have ………………. parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ……….. .
Solution:

NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.1 PDF Q2

Ex 10.1 Class 10 Maths Question 3.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) 119−−−√ cm
Solution: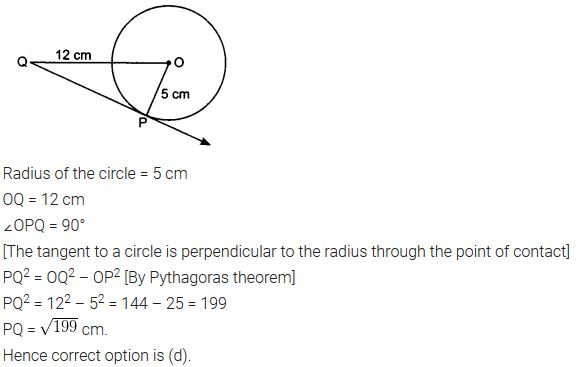
Ex 10.1 Class 10 Maths Solutions NCERT PDF Q3

Note: PQ = √119

Ex 10.1 Class 10 Maths Question 4.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution: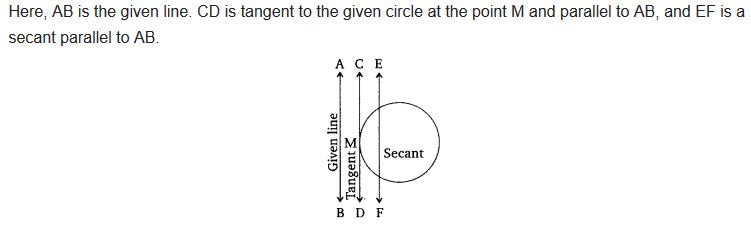
Exercise 10.1 Class 10 Maths Solutions NCERT PDF Q4

New Syllabus- Class 10 Maths Circles Ex 10.1(CBSE)

Question 1:

In a circle with center O, a tangent PT is drawn at point P on the circle. If the radius of the circle is 5 cm and the length of the tangent PT is 12 cm, find the length of OP.

Solution:

We know that the radius of the circle is perpendicular to the tangent at the point of contact. Therefore, ∠OTP = 90°.

We can use the Pythagorean theorem in right triangle OTP:

OT² = OP² + PT²

Substituting the values:
5² = OP² + 12²
25 = OP² + 144
OP² = 25 – 144 = -119 (This is not possible in this case. It seems like there might be a mistake in the question. Please confirm the data.)

Question 2:

Find the length of the tangent from a point 13 cm away from the center of a circle with a radius of 5 cm.

Solution:

Let the point be P and the point of contact of the tangent be T. The distance from the center O to the point P is 13 cm, and the radius of the circle is 5 cm.

We can use the Pythagorean theorem in the right-angled triangle OTP, where OT is the radius, PT is the tangent, and OP is the distance from the center to the point.

OP² = OT² + PT²

Substitute the known values:
13² = 5² + PT²
169 = 25 + PT²
PT² = 169 – 25 = 144
PT = √144 = 12 cm

So, the length of the tangent is 12 cm.

Question 3:

A circle with center O has a radius of 6 cm. From a point P outside the circle, two tangents PA and PB are drawn. If the length of the tangents from point P to the circle is 8 cm each, find the distance from point P to the center O of the circle.

Solution:

We know that the tangents from an external point to a circle are equal in length. Thus, PA = PB = 8 cm. Also, the radius OP is perpendicular to the tangent at the point of contact.

In right triangle OPA:
OP² = OA² + PA²

Since the radius of the circle is 6 cm, OA = 6 cm, and PA = 8 cm:
OP² = 6² + 8² = 36 + 64 = 100
OP = √100 = 10 cm

So, the distance from point P to the center O is 10 cm.

Question 4:

If two tangents are drawn from an external point to a circle, prove that the two tangents are equal in length.

Solution:

Let the two tangents from an external point P be PA and PB, and let O be the center of the circle. We need to prove that PA = PB.

First, draw the radii OA and OB, which are perpendicular to the tangents at points A and B, respectively. Therefore, ∠OAP = ∠OBP = 90°.

Now, consider the triangles OAP and OBP:

  • OA = OB (radii of the same circle)
  • OP is common
  • ∠OAP = ∠OBP = 90° (since the radius is perpendicular to the tangent)

By the RHS criterion of congruence, we have:
ΔOAP ≅ ΔOBP

Thus, by congruence, we can say:
PA = PB

Therefore, the two tangents drawn from an external point to a circle are equal in length.

Class 10 Maths Circles Mind Map

Introduction

A circle is a set of all points in a plane at a fixed distance from a fixed point in a plane. The fixed point is called the centre of the circle. The fixed distance is called the radius of the circle.

Line and a Circle

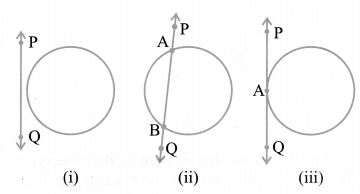
NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.1 Mind Map 1
In Fig. (i), the line PQ and the circle have no common point. In this case, PQ is called a non-intersecting line with respect to the circle. In Fig. (ii), there are two common points A and B that the line PQ and the circle have. In this case, we call the line PQ a secant of the circle. In Fig. (iii), there is only one point A which is common to the line PQ and the circle. In this case, the line is called a tangent to the circle.

Tangent

A tangent to a circle is a straight line which touches the circle at only one point. The point where the tangent touches the circle is called point of contact of the tangent to the circle.
A tangent to a circle is a special case of a secant, when the two ends points of its corresponding chord coincides.
Theorem: Tangent at any point on a circle is perpendicular to the radius through the point of contact.

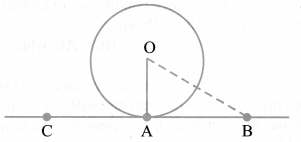
NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.1 Mind Map 2

CB is the tangent to the given circle touching at A and OA is the radius.
∴ ∠OAB = 90°
(i) At any point on the circle there can be one and only one tangent.
(ii) The line containing the radius through the point of contact is called the normal to the circle at the point.

Number of Tangents from a Point to Circle

(i) No tangent can be drawn from the point lying inside the circle, as shown in fig. (i)
(ii) One and only one tangent can be drawn from a point lying on the circle, as shown in fig. (ii)
(iii) Only two tangents can be drawn from an exterior point to a circle, as shown in fig. (iii)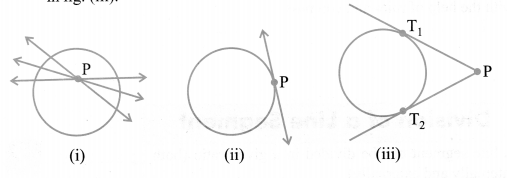
NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.1 Mind Map 3

Length of a Tangent

The length of the segment of a tangent from an external point to the point of contact with the circle is called the length of the tangent

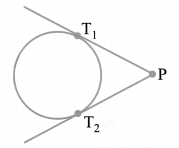
NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.1 Mind Map 4
In the given figure, T1 and T2 are the points of contact of the tangents PT1 and PT2 respectively from the external point P.

Theorem Related to Length of Tangents From the External Points

The lengths of tangents drawn from an external point to a circle are equal.
i.e.,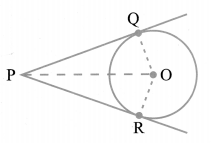
NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.1 Mind Map 5
Here, PQ and PR are the two tangents drawn from P to the circle

📘 Math & Science Solutions by Class

🔹 Class 10

🔹 Class 9

🔹 Class 8

🔹 Class 7

🔹 Class 6

🔹 Class 12

🔹 Class 11

You can access the official NCERT Solutions for Class 10 Mathematics on the NCERT website at the following link:

NCERT Class 10 Mathematics Solutions

📘 Math & Science Solutions by Class

🔹 Class 10

🔹 Class 9

🔹 Class 8

🔹 Class 7

🔹 Class 6

🔹 Class 12

🔹 Class 11

Learn more about circle formulas from NCERT.

Class-wise Solutions

Class 12:

Class 12 Physics – NCERT Solutions

Class 12 Chemistry – NCERT Solutions

Class 11:

Class 10:

Class 9:

Class 8:

Class 7:

Class 6:

Subject-wise Solutions

Physics:

Chemistry:

Biology:

Math:

Science:

NEET BIOLOGY