In Class 10 Maths Ex 4.4 Ch Quadratic Equation Answers, Exercise 4.4 focuses on solving quadratic equations by using the quadratic formula. This method is especially useful when the equation cannot be easily factorized. The general form of a quadratic equation is ax² + bx + c = 0,
helps us find the roots of the equation accurately.
In this exercise, you will practice applying the formula to different types of quadratic equations and learn how to identify the nature of roots using the discriminant (D = b² – 4ac). This is an important topic for board exams and helps in understanding further algebraic concepts.
Class 10 Maths Ex 4.4 Ch Quadratic Equation- Textbook
1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) 2x² -3x + 5 = 0
(ii) 3x2 – 4√3x + 4 = 0
(iii) 2x2-6x + 3 = 0
Solution:

Ex 4.4 Class 10 Maths Question 2.
Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(1) 2x2 + kx + 3 = 0
(2) kx (x – 2) + 6 = 0
Solution:
Ex 4.4 Class 10 Maths Question 3.
Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m2? If so, find its length and breadth.
Solution:
Ex 4.4 Class 10 Maths Question 4.
Is the following situation possible? If so, determine their present ages.
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution: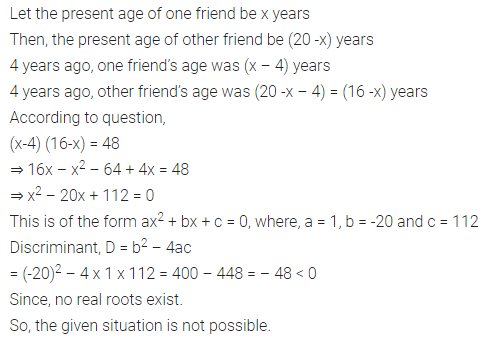
Ex 4.4 Class 10 Maths Question 5.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so, find its length and breadth.
Solution:
New Syllabus – Class 10 Maths Ex 4.4 Ch Quadratic Equation Answers
Question 1: Find the nature of the roots of the following quadratic equations. If real roots exist, find them:
(i) 2x² – 3x + 5 = 0
Solution:
For the quadratic equation 2x² – 3x + 5 = 0, we have:
- a = 2
- b = -3
- c = 5
The discriminant (Δ) is given by:
Δ = b² – 4ac = (-3)² – 4(2)(5) = 9 – 40 = -31
Since Δ < 0, the equation has no real roots.
(ii) 3x² – 4x + 4 = 0
Solution:
For the quadratic equation 3x² – 4x + 4 = 0, we have:
- a = 3
- b = -4
- c = 4
The discriminant (Δ) is:
Δ = b² – 4ac = (-4)² – 4(3)(4) = 16 – 48 = -32
Since Δ < 0, the equation has no real roots.
(iii) 2x² – 6x + 3 = 0
Solution:
For the quadratic equation 2x² – 6x + 3 = 0, we have:
- a = 2
- b = -6
- c = 3
The discriminant (Δ) is:
Δ = b² – 4ac = (-6)² – 4(2)(3) = 36 – 24 = 12
Since Δ > 0, the equation has two distinct real roots.
To find the roots, we use the quadratic formula:
x = (-b ± √Δ) / 2a
x = (-(-6) ± √12) / 2(2) = (6 ± 2√3) / 4 = (3 ± √3) / 2
Thus, the roots are:
x = (3 + √3) / 2 or x = (3 – √3) / 2
Question 2: Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x² + kx + 3 = 0
Solution:
For the quadratic equation 2x² + kx + 3 = 0, the condition for two equal roots is that the discriminant Δ = 0.
The discriminant is:
Δ = b² – 4ac
Here, a = 2, b = k, and c = 3, so:
Δ = k² – 4(2)(3) = k² – 24
For two equal roots, Δ = 0:
k² – 24 = 0
k² = 24
k = ±√24 = ± 2√6
Thus, the values of k are k = 2√6 or k = -2√6.
(ii) kx(x – 2) + 6 = 0
Solution:
First, expand the equation:
kx(x – 2) + 6 = 0 → kx² – 2kx + 6 = 0
For this quadratic equation to have two equal roots, the discriminant must be zero. So:
Δ = b² – 4ac = 0
Here, a = k, b = -2k, and c = 6. The discriminant is:
Δ = (-2k)² – 4(k)(6) = 4k² – 24k
For two equal roots, Δ = 0:
4k² – 24k = 0
4k(k – 6) = 0
Thus, k = 0 or k = 6.
Therefore, the values of k are k = 0 or k = 6.
To sum up, Class 10 Maths Ex 4.4 Ch Quadratic Equation plays a vital role in strengthening your understanding of solving quadratic equations using the quadratic formula. This method is particularly useful when factorization is not easy or possible.
Through this exercise, students learn how to identify the values of a, b, and c in the standard form of the equation and substitute them into the quadratic formula to find the roots. The concept of the discriminant (D = b² – 4ac) also helps in determining whether the roots are real and distinct, real and equal, or imaginary.
By practicing Class 10 Maths Ex 4.4 Ch Quadratic Equation, students gain confidence in applying formulas, calculating square roots, and simplifying expressions. These skills are essential not just for board exams but also for future topics in mathematics, including coordinate geometry and polynomials. This exercise builds a strong foundation in algebra and improves problem-solving speed and accuracy.
Furthermore, Class 10 Maths Ex 4.4 Ch Quadratic Equation encourages logical thinking and a step-by-step approach to solving mathematical problems. It also improves your ability to check the correctness of roots by substituting them back into the original equation. This helps avoid careless mistakes and boosts exam performance.
In conclusion, Class 10 Maths Ex 4.4 Ch Quadratic Equation is more than just an academic requirement; it is a critical stepping stone for mastering higher-level math concepts. Regular practice of this exercise ensures a thorough grasp of the quadratic formula, helps identify the nature of roots, and prepares students well for board exams and competitive tests. So, make sure to revise and solve every question with clarity and focus.
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
