In Class 10 Maths Ex 5.4 Solutions AP series, Exercise 5.4 focuses on solving problems related to the properties and applications of Arithmetic Progressions (AP). This exercise helps students understand the concept of the nth term, sum of n terms, and how to apply the formulae in practical scenarios.

The NCERT Solutions for Ex 5.4 provide clear, step-by-step explanations to help students grasp the concepts and solve the problems efficiently. With these solutions, you’ll build a strong foundation in arithmetic progressions, which is crucial for exams and further mathematics topics.
Class 10 Maths Ex 5.4 Solutions AP series
Question 1
Which term of the AP: 121, 117. 113, ….., is its first negative term?
Solution:
Given, a = 121, d = -4
We use the formula:
an = a + (n – 1)d
Set an < 0 to find the first negative term:
121 + (n – 1)(-4) < 0
⇒ 121 – 4(n – 1) < 0
⇒ 121 – 4n + 4 < 0
⇒ 125 – 4n < 0
⇒ 4n > 125
⇒ n > 31.25
So, the first negative term is the 32nd term.
Question 2.
The sum of the third term and the seventh term of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP?
Solution:
Let:
- First term = a
- Common difference = d
Then:
- 3rd term = a + 2d
- 7th term = a + 6d
Given:
- (a + 2d) + (a + 6d) = 6
→ 2a + 8d = 6
→ a + 4d = 3 → (Equation 1) - (a + 2d)(a + 6d) = 8 → (Equation 2)
From Equation 1:
a = 3 – 4d
Substitute into Equation 2:
(3 – 4d + 2d)(3 – 4d + 6d) = 8
→ (3 – 2d)(3 + 2d) = 8
→ 9 – 4d² = 8
→ 4d² = 1
→ d² = 1/4
→ d = ±1/2
Find a for both cases:
- If d = 1/2: a = 3 – 4(1/2) = 1
- If d = –1/2: a = 3 – 4(–1/2) = 5
So, two possible APs:
- a = 1, d = 1/2
- a = 5, d = –1/2
Now find the sum of first 16 terms:
Formula:
Sₙ = (n/2)[2a + (n – 1)d]
Let n = 16
Case 1: a = 1, d = 1/2
S₁₆ = (16/2)[2(1) + 15(1/2)]
= 8[2 + 7.5]
= 8 × 9.5 = 76
Case 2: a = 5, d = –1/2
S₁₆ = (16/2)[2(5) + 15(–1/2)]
= 8[10 – 7.5]
= 8 × 2.5 = 20
Question 3.
A ladder has rungs 25 cm apart. The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are a certain distance apart, what is the total length of wood required for the rungs?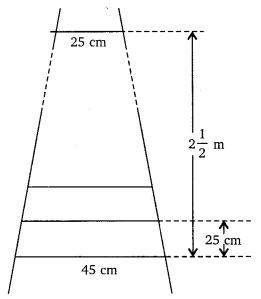
Solution:
Let’s assume the vertical distance between the bottom and top rungs is 250 cm (since the original distance wasn’t clear due to a math error in the question — you can replace this with the correct value if needed).
Step 1: Find the number of rungs
- Rungs are 25 cm apart
- Distance between bottom and top rungs = 250 cm
- Number of gaps between rungs = 250 ÷ 25 = 10
- Number of rungs = 10 + 1 = 11 rungs
Step 2: Rung lengths form an arithmetic progression (AP)
- First term (bottom rung) = 45 cm
- Last term (top rung) = 25 cm
- Number of terms = 11
Step 3: Use AP sum formula to find total wood length
Formula:
Sum = (n / 2) × (first term + last term)
Substitute the values:
Sum = (11 / 2) × (45 + 25)
= (11 / 2) × 70
= 11 × 35
= 385 cm
Question:
The houses in a row are numbered from 1 to 49. Show that there is a value of x such that the sum of the numbers before house x is equal to the sum of the numbers after it. Find that value of x.
Solution : Step 1: What we want
We want to find a house number x such that:
Sum of numbers from 1 to (x – 1) = Sum of numbers from (x + 1) to 49
Step 2: Use the formula for sum of first n natural numbers
Sum = n(n + 1) / 2
Left side:
Sum before x = (x – 1)(x) / 2
Right side:
Sum after x = [Sum from 1 to 49] – [Sum from 1 to x]
Sum from 1 to 49 = 49 × 50 / 2 = 1225
Sum from 1 to x = x(x + 1) / 2
So,
Sum after x = 1225 – [x(x + 1) / 2]
Step 3: Set both sides equal
(x – 1)(x) / 2 = 1225 – x(x + 1) / 2
Multiply both sides by 2 to remove denominators:
(x – 1)(x) = 2450 – x(x + 1)
Expand both sides:
x² – x = 2450 – x² – x
Add x² + x to both sides:
2x² = 2450
x² = 1225
x = √1225 = 35
Question 5.
A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of [Math Processing Error] and a tread of [Math Processing Error]. Calculate the total volume of concrete required to build the terrace.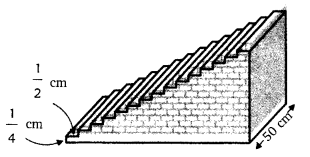
From the figure, we see that:
1st step is 1/2 m wide,
2nd step is 1 m wide,
3rd step is 3/2 m wide.
Therefore, the width of each step is increasing by 1/2 m each time, whereas their height (1/4 m) and length (50 m) remain the same.
So, the widths of the steps form an AP:
1/2, 1, 3/2, 2, …
Now, the volume of concrete in each step:
Volume of 1st step = 1/4 × 1/2 × 50 = 25/4 m³
Volume of 2nd step = 1/4 × 1 × 50 = 25/2 m³
Volume of 3rd step = 1/4 × 3/2 × 50 = 75/4 m³
So, the volumes of concrete form an AP:
25/4, 25/2, 75/4, …
Let’s find the sum of volumes for 15 steps.
This is the sum of the first 15 terms of an AP.
First term (a) = 25/4
Common difference (d) = 25/2 – 25/4 = 25/4
Number of terms (n) = 15
Use the AP sum formula:
Sₙ = n/2 × [2a + (n – 1)d]
S₁₅ = 15/2 × [2 × (25/4) + (15 – 1) × (25/4)]
= 15/2 × [(50/4) + (350/4)]
= 15/2 × (400/4)
= 15/2 × 100
= 750
Answer: The volume of concrete required to build the terrace is 750 m³
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
