Master Class 11 Math Ch 1 Sets Ex 1.1 To Ex 1.6

Welcome to Class 11 Math Ch 1 Sets Ex 1.1 to Ex 1.6, where we explore the foundational concept of modern mathematics. This chapter introduces you to the idea of sets, a collection of well-defined objects or elements, which is widely used in mathematics and computer science.

Class 11 Math Ch 1 Sets Ex 1.1 to Ex 1.6 - NCERT Solutions

In this page, you will find NCERT solutions for Exercises 1.1 to 1.6, explained step-by-step in an easy-to-understand manner. These solutions are designed as per the latest CBSE curriculum to help students strengthen their understanding and perform well in exams.

Whether you’re preparing for your school tests or building your concepts for competitive exams like JEE or CUET, these solutions will help you master important topics such as:

Types of sets (empty, finite, infinite)
Venn diagrams
Union, intersection, and difference of sets
Complement of a set
Cartesian product of sets

Let’s begin your journey through the world of sets with clear concepts and accurate NCERT-based solutions.

Class 11 Math Ch 1 Sets Ex 1.1 to Ex 1.6 Full Chapter Answers

Q.1: Which of the following are sets? Explain your answer.

(a) The collection of all days in a week which have the first letter S.
Yes, it is a set. The collection is well-defined as the days starting with ‘S’ are Sunday and Saturday.

(b) The collection of ten most famous singers of India.
No, it is not a set. The term “most famous” is subjective and can vary from person to person, so the collection is not well-defined.

(c) A group of best football strikers of the world.
No, it is not a set. The term “best” is not clearly defined and can differ based on opinion, making the collection vague.

(d) The collection of all girls in your school.
Yes, it is a set. The collection is well-defined as all girls in a school can be listed specifically.

(e) The collection of all odd numbers below 50.
Yes, it is a set. The collection is well-defined and includes numbers like 1, 3, 5, …, 49.

(f) A collection of poems written by the poet Shakespeare.
Yes, it is a set. The poems written by Shakespeare are documented and can be listed clearly.

(g) The collection of all prime numbers.
Yes, it is a set. Prime numbers are defined mathematically, so the collection is well-defined.

(h) The collection of questions in a science book.
Yes, it is a set. The questions are printed in the book and are clearly listed.

(i) A collection of most dangerous reptiles in India.
No, it is not a set. The term “most dangerous” is not specific and can vary, making the collection ill-defined.

Ex 1.1 Class 11 Maths Q.2: Let P = {2, 3, 4, 5, 6, 7}. Insert the correct symbol ∈or∉ inside the given blank spaces below:
(a). 2 . . . . . . . . . . P
(b). 9 . . . . . . . . . P
(c). 11 . . . . . . . . P
(d). 4 . . . . . . . . P
(e). 0 . . . . . . . . P
(f). 7 . . . . . . . . P

Solution:
(i) 5 ∈ A
(ii) 8 ∉ A
(iii) 0 ∉ A
(iv) 4 ∈ A
(v) 2 ∈ A
(vi) 10 ∉ A

Ex 1.1 Class 11 Maths Q.3: Write the given sets in roster form:
(a). P = {y: y is an integer and -4 < y < 6}.
(b). Q = {y: y is a natural number which is <8}
(c). R = {y: y is a 2 digit natural number in which the sum of its digits is 9}
(d). S = {y: y is a prime number which is a divisor of 70}
(e). T = The set of all letters in the word ELEPHANT

(f). U = The set of all letters in the word DIVISION

Solution:
(a) P = {y: y is an integer and -4 < y < 6}
Integers between -4 and 6 are:
P = {–3, –2, –1, 0, 1, 2, 3, 4, 5}

(b) Q = {y: y is a natural number which is < 8}
Natural numbers less than 8 are:
Q = {1, 2, 3, 4, 5, 6, 7}

(c) R = {y: y is a 2-digit natural number in which the sum of its digits is 9}
Two-digit numbers whose digits add to 9 are:
R = {18, 27, 36, 45, 54, 63, 72, 81, 90}

(d) S = {y: y is a prime number which is a divisor of 70}
First, prime factorization of 70 = 2 × 5 × 7
S = {2, 5, 7}

(e) T = The set of all letters in the word ELEPHANT
Unique letters in “ELEPHANT”:
T = {E, L, P, H, A, N, T}

(f) U = The set of all letters in the word DIVISION
Unique letters in “DIVISION”:
U = {D, I, V, S, O, N}

Ex 1.1 Class 11 Maths Q.4: Write the given sets in set-builder form:
(a). {4, 8, 12, 16, 20}
(b). {3, 9, 27, 81}
(c). {4, 16, 64, 256, 1024}
(d). {1, 3, 5, 7…}
(e). {1, 8, 27, 64….1000}

Solution:
(a) {4, 8, 12, 16, 20}
This is the set of all positive multiples of 4 up to 20.
Set-builder form:
A = {x : x = 4n, n ∈ N and 1 ≤ n ≤ 5}

(b) {3, 9, 27, 81}
These are powers of 3.
Set-builder form:
B = {x : x = 3ⁿ, n ∈ N and 1 ≤ n ≤ 4}

(c) {4, 16, 64, 256, 1024}
These are powers of 4.
Set-builder form:
C = {x : x = 4ⁿ, n ∈ N and 1 ≤ n ≤ 5}

(d) {1, 3, 5, 7…}
This is the set of all odd natural numbers.
Set-builder form:
D = {x : x = 2n – 1, n ∈ N}

(e) {1, 8, 27, 64…1000}
These are cubes of natural numbers from 1 to 10: 1³ to 10³.
Set-builder form:
E = {x : x = n³, n ∈ N and 1 ≤ n ≤ 10}

Ex 1.1 Class 11 Maths Q.5: List all the elements of the following sets :
(i) A = {x : x is an odd natural number}
This is an infinite set as it includes all odd natural numbers:
A = {1, 3, 5, 7, 9, 11, 13, …}

(iii) C = {x : x is an integer, x² < 4}
We need integers whose square is less than 4.
Possible values:

x² < 4 ⇒ x ∈ {–1, 0, 1}
C = {–1, 0, 1}

(iv) D = {x : x is a letter in the word “LOYAL”}
Unique letters in the word “LOYAL”:
D = {L, O, Y, A}

(v) E = {x : x is a month of a year not having 31 days}
Months that do not have 31 days:

April (30), June (30), September (30), November (30), February (28/29)
E = {February, April, June, September, November}

(vi) F = {x : x is a consonant in the English alphabet which precedes k}
Letters before ‘k’ in the alphabet: a, b, c, d, e, f, g, h, i, j
Consonants among them: b, c, d, f, g, h, j
F = {b, c, d, f, g, h, j}

Ex 1.1 Class 11 Maths Q.6: Match the following:

(A)	{1, 2, 3, 6}	(i)	{y: y is a divisor of 6 and also a prime number}
(B)	{T, R, I, G, O, N, M, E, Y}	(ii)	{y: y is less than 10 and also an odd number}
(C)	{2, 3}	(iii)	{y: y is natural number divisor of 6}
(D)	{1, 3, 5, 7, 9}	(iv)	{y: y is a letter of the word TRIGONOMETRY}

Solution:

Given Sets and Options:

(A) {1, 2, 3, 6}
(B) {T, R, I, G, O, N, M, E, Y}
(C) {2, 3}
(D) {1, 3, 5, 7, 9}

(i) {y: y is a divisor of 6 and also a prime number}
(ii) {y: y is less than 10 and also an odd number}
(iii) {y: y is natural number divisor of 6}
(iv) {y: y is a letter of the word TRIGONOMETRY}

Correct Matchings:

(A) {1, 2, 3, 6} → (iii) {y: y is natural number divisor of 6}
(B) {T, R, I, G, O, N, M, E, Y} → (iv) {y: y is a letter of the word TRIGONOMETRY}
(C) {2, 3} → (i) {y: y is a divisor of 6 and also a prime number}
(D) {1, 3, 5, 7, 9} → (ii) {y: y is less than 10 and also an odd number}

Class 11 Math Ch 1 Sets Ex 1.2 – Textbook Solutions

Class 11 Maths Q.1: Which of the following given below is null set?
(i). Set of odd natural numbers which is divisible by 2.
(ii). Set of even numbers which are prime
(iii). {x: x is a natural number, x<5 and x>7}
(iv). {y: y is a point common to any two parallel lines}

Solution:
i) Set of odd natural numbers which is divisible by 2
→ Null set
Odd numbers are never divisible by 2, so no such number exists.
Set = Ø

(ii) Set of even numbers which are prime
→ Not a null set
2 is an even number and also a prime number.
Set = {2}, so not a null set

(iii) {x: x is a natural number, x < 5 and x > 7}
→ Null set
No natural number can be less than 5 and greater than 7 at the same time.
Set = Ø

(iv) {y: y is a point common to any two parallel lines}
→ Null set
Parallel lines never intersect, so they do not have any common point.
Set = Ø

Ex 1.2 Class 11 Maths Q.2: State whether the following sets are infinite or finite:
(i). A set of months of a year.
(ii). {1, 2, 3 ….}
(iii). {1, 2, 3…99, 100}
(iv). The set of positive integers which are greater than 100.
(v). The set of prime numbers which are less than 99

Solution:
(i) A set of months of a year
→ Finite set
There are exactly 12 months in a year.
Answer: Finite

(ii) {1, 2, 3, …}
→ Infinite set
This set continues without an end, representing all natural numbers.
Answer: Infinite

(iii) {1, 2, 3, …, 99, 100}
→ Finite set
It contains 100 elements, from 1 to 100.
Answer: Finite

(iv) The set of positive integers which are greater than 100
→ Infinite set
There is no end to positive integers greater than 100.
Answer: Infinite

(v) The set of prime numbers which are less than 99
→ Finite set
There are only a limited number of prime numbers less than 99.
Answer: Finite

Ex 1.2 Class 11 Maths Q.3: State whether the following sets are infinite or finite:
(i). The set of lines parallel to the x – axis.
(ii). The set of letters in the vowels.
(iii). The set of numbers multiple of 10.
(iv). The set of humans living on Earth.
(v). The set of circles passing through the origin (0, 0).

Solution:
(i) The set of lines parallel to the x-axis
There are infinitely many lines parallel to the x-axis (one at each value of y).
Answer: Infinite

(ii) The set of letters in the vowels
Vowels in English are {A, E, I, O, U} → total of 5 letters.
Answer: Finite

(iii) The set of numbers multiple of 10
Multiples of 10 are infinite: {10, 20, 30, 40, …}
Answer: Infinite

(iv) The set of humans living on Earth
Although a large number, the human population is countable and limited.
Answer: Finite

(v) The set of circles passing through the origin (0, 0)
There are infinitely many circles that can pass through the origin (with different centers and radii).
Answer: Infinite

Ex 1.2 Class 11 Maths Q.4: In the following set given below, state whether A = B or not:
(i). A = {w, x, y, z}
B = {z, y, x, w}
(ii). A = {5, 9, 13, 17}
B = {9, 5, 17, 19}
(iii). A = {4, 2, 6, 10, 8}
B = {x: x is positive even integer and x≤10 }
(iv). A = {x: x is a multiple of 10}
B = {10, 15, 20, 25, 30 …}

Solution:
(i) A = {w, x, y, z}, B = {z, y, x, w}

Both sets have exactly the same elements, just in different order.
A = B

(ii) A = {5, 9, 13, 17}, B = {9, 5, 17, 19}

Elements in A: 5, 9, 13, 17
Elements in B: 5, 9, 17, 19
Different elements (13 ≠ 19)
so, A ≠ B

(iii) A = {4, 2, 6, 10, 8}, B = {x : x is positive even integer and x ≤ 10}

B describes the set of all positive even integers ≤ 10 → {2, 4, 6, 8, 10}
A and B have exactly the same elements.
so, A = B

(iv) A = {x : x is a multiple of 10}, B = {10, 15, 20, 25, 30, …}

A: multiples of 10 → {10, 20, 30, 40, …}
B: not just multiples of 10; includes 15, 25 (not multiples of 10)
so,A ≠ B

Ex 1.2 Class 11 Maths Q.5 In the following set given below, is the pair of sets equal?
(i). A = {3, 4}
B = {y: y is solution of y²+5y+6=0}
(ii). A = {a: a is a letter in the word FOLLOW}
B = {b: b is a letter in the word WOLF}

Solution:
(i) A = {3, 4}, B = {y: y is a solution of y² + 5y + 6 = 0}

Let’s solve the quadratic equation:

= y2+5y+6=0

⇒(y+2)(y+3)=0

⇒y=–2,–3

So,
B = {–2, –3} and
A = {3, 4}

Since the elements of A and B are different,
so, A ≠ B

(ii) A = {a: a is a letter in the word FOLLOW}

Letters in FOLLOW: F, O, L, L, O, W → removing duplicates → {F, O, L, W}

B = {b: b is a letter in the word WOLF}
Letters in WOLF: W, O, L, F → {W, O, L, F}

So,
A = {F, O, L, W} = B

Since both sets have exactly the same elements,
so, A = B

Ex 1.2 Class 11 Maths Q.6: From the following sets, select equal sets:
A = {2, 4, 8, 12}
B = {1, 2, 3, 4}
C = {4, 8, 12, 14}
D = {3, 1, 4, 2}
E = {–1, 1}
F = {0, a}
G = {1, –1}
H = {0, 1}

Solution:
Step-by-step solution:

Compare A and C
A = {2, 4, 8, 12}
C = {4, 8, 12, 14}
→ Not equal (A has 2, C has 14 which is not in A)
Compare B and D
B = {1, 2, 3, 4}
D = {3, 1, 4, 2}
→ Equal (All elements are same, just in different order)
Compare E and G
E = {–1, 1}
G = {1, –1}
→ Equal (Same elements, different order doesn’t matter)
Compare F and H
F = {0, a}
H = {0, 1}
→ Not equal (F contains the letter ‘a’, H contains the number 1)

Final Answer:

Equal sets are:

E = G

B = D

Class 11 Maths NCERT Solutions Chapter 1 Sets Ex 1.3

Ex 1.3 Class 11 Maths Q.1: Fill in the blanks properly using ⊂ and ⊄.
(i). {3, 4, 5} ____ {2, 3, 4, 5, 6}
(ii). {a, b, c} ____ {d, c, d}
(iii). {y: y is a pupil of Class 11 of the school} ____ {y: y is students of the school}
(iv). {y: y is a circle in the plane} ____ {y: y is a circle in the same plane with radius 2 unit}
(v). {y: y is an equilateral triangle in a plane} ____ {y: y is a rectangle in the same plane}
(vi). {y: y is an equilateral triangle in a plane} ____ {y: y is a triangle in the plane}
(vii). {y: y is an odd natural number} ____ {x: x is an integers}

Solution:
(ii) {a, b, c} ⊄ {d, c, d}
Explanation: ‘a’ and ‘b’ are not in the second set.

(iii) {y: y is a pupil of Class 11 of the school} ⊂ {y: y is a student of the school}
Explanation: Every Class 11 pupil is a student of the school.

(iv) {y: y is a circle in the plane} ⊄ {y: y is a circle in the same plane with radius 2 unit}
Explanation: All circles in the plane are not of radius 2. So not a subset.

(v) {y: y is an equilateral triangle in a plane} ⊄ {y: y is a rectangle in the same plane}
Explanation: Triangles are not rectangles. Different shapes.

(vi) {y: y is an equilateral triangle in a plane} ⊂ {y: y is a triangle in the plane}
Explanation: All equilateral triangles are triangles.

(vii) {y: y is an odd natural number} ⊂ {x: x is an integer}
Explanation: Every odd natural number is also an integer.

Ex 1.3 Class 11 Maths Q.2: State whether the given statements are true or false:
(i). {b, c} ⊄ {c, d, e}
(ii). {a, e, i} ⊂ {x: x is a vowel in the English alphabets}
(iii). {1, 2, 3} ⊂{1, 2, 4, 5}
(iv). {c} ⊂ {b, c, d}
(v). {b} ∈ {a, b, c, d}
(vi). {y: y is an even natural no. less than 6} ⊂ {y: y is a natural no. which can divide 36}

Solution:
(i) {b, c} ⊄ {c, d, e}
→ True, because ‘b’ is not in the second set.

(ii) {a, e, i} ⊂ {x: x is a vowel in the English alphabets}
→ True, because a, e, i are vowels.

(iii) {1, 2, 3} ⊂ {1, 2, 4, 5}
→ False, because 3 is not in the second set.

(iv) {c} ⊂ {b, c, d}
→ True, because c is present in the second set.

(v) {b} ∈ {a, b, c, d}
→ False, because {b} is a set and not an element. ‘b’ ∈ {a, b, c, d} would be true.

(vi) {y: y is an even natural number less than 6} ⊂ {y: y is a natural number which can divide 36}
→ Even natural numbers less than 6 are {2, 4}
Divisors of 36 are {1, 2, 3, 4, 6, 9, 12, 18, 36}
→ {2, 4} ⊂ {1, 2, 3, 4, 6, 9, 12, 18, 36} → True

Ex 1.3 Class 11 Maths Q.3: Let X = {11, 12, {13, 14}, 15}. According to the given set which of the given statements are false? Explain why.
(i). {13, 14} ⊂ X
(ii). {13, 14} ∈ X
(iii). {{13, 14}} ⊂ X
(iv). 11 ∈ X
(v). 11 ⊂ X
(vi). {11, 12, 15} ⊂ X
(vii). {11, 12, 15} ∈ X
(viii). {11, 12, 13} ⊂ X
(ix). Ø ∈ X
(x). Ø ⊂ X
(xi). {Ø} ⊂ X

Solution:

Let
X = {11, 12, {13, 14}, 15}

That means X has four elements:

(i) {13, 14} ⊂ X
False
→ {13, 14} is not a subset of X because neither 13 nor 14 are elements of X.
→ X contains the set {13, 14} as a single element, not 13 or 14 individually.

(ii) {13, 14} ∈ X
True
→ The set {13, 14} is an element of X.

(iii) {{13, 14}} ⊂ X
True
→ {{13, 14}} is a set containing the set {13, 14} as its only element, and since {13, 14} ∈ X, it is a valid subset.

(iv) 11 ∈ X
True
→ 11 is directly an element of X.

(v) 11 ⊂ X
False
→ 11 is not a set; hence it can’t be a subset

(vi) {11, 12, 15} ⊂ X
True
→ All elements 11, 12, and 15 are elements of X.

(vii) {11, 12, 15} ∈ X
False
→ X has 11, 12, 15 as individual elements, not as a single set.

(viii) {11, 12, 13} ⊂ X
False
→ 13 is not an element of X.

(ix) Ø ∈ X
False
→ The empty set is not an element of X.

(x) Ø ⊂ X
True
→ The empty set is a subset of every set.

(xi) {Ø} ⊂ X
False
→ X does not contain Ø as an element, so {Ø} is not a subset.

Ex 1.3 Class 11 Maths Q.4: Write all the subsets of the given sets:
(i). {b}
(ii). {b, c}
(iii). {2, 3, 4}
(iv). Ø

Solution:
(i) {b}

A set with 1 element has 21=22^1 = 221=2 subsets:

Subsets:
→ Ø, {b}

(ii) {b, c}

A set with 2 elements has 22=42^2 = 422=4 subsets:

Subsets:
→ Ø, {b}, {c}, {b, c}

(iii) {2, 3, 4}

A set with 3 elements has 23=82^3 = 823=8 subsets:

Subsets:
→ Ø, {2}, {3}, {4}, {2, 3}, {2, 4}, {3, 4}, {2, 3, 4}

(iv) Ø

The empty set has only one subset, which is itself.

Subsets:
→ Ø

Ex 1.3 Class 11 Maths Q.5: How many elements has P(X), if X = Ø ?

Solution:
P(X) means the power set of set X.

The power set of a set with n elements has 2ⁿ elements.

Here,
X = Ø, which means X has 0 elements.

So,
n = 0
⇒ Number of elements in P(X) = 2⁰ = 1

Ex 1.3 Class 11 Maths Q.6: Write the given in the form of intervals:
(i). {y: y ∈ R, –5 < y ≤ 7}
(ii). {y: y ∈ R, –13 < y < –11}
(iii). {y: y ∈ R, 1 ≤ y < 8}
(iv). {y: y ∈ R, 4 ≤ y ≤ 5}

Solution:
(i) {y ∈ ℝ : –5 < y ≤ 7}

Interval form:
→ (–5, 7]

(ii) {y ∈ ℝ : –13 < y < –11}

Interval form:
→ (–13, –11)

(iii) {y ∈ ℝ : 1 ≤ y < 8}

Interval form:
→ [1, 8)

(iv) {y ∈ ℝ : 4 ≤ y ≤ 5}

Interval form:
→ [4, 5]

Ex 1.3 Class 11 Maths Q.7: Write the given intervals in the form of set – builder:
(i). (–4, 1)
(ii). [7, 13]
(iii). (7, 13]
(iv). [–24, 6)

Solution:
(i) (–4, 1)

Set-builder form:
→ {x ∈ ℝ : –4 < x < 1}

(ii) [7, 13]

Set-builder form:
→ {x ∈ ℝ : 7 ≤ x ≤ 13}

(iii) (7, 13]

Set-builder form:
→ {x ∈ ℝ : 7 < x ≤ 13}

(iv) [–24, 6)

Set-builder form:
→ {x ∈ ℝ : –24 ≤ x < 6}

Ex 1.3 Class 11 Maths Q.8: What universal set/ sets would you propose for the given sets?

(i). The set of right triangles
(ii). The set of isosceles triangles

Solution:
(i) The set of right triangles

Proposed Universal Set:
→ The set of all triangles
(i.e., U = {x : x is a triangle})

Because all right triangles are a part of the larger group of all triangles.

(ii) The set of isosceles triangles

Proposed Universal Set:
→ The set of all triangles
(i.e., U = {x : x is a triangle})

Since isosceles triangles are a specific type of triangle, the universal set should again be all triangles.

Ex 1.3 Class 11 Maths Q.9: X = {1, 3, 5}, Y = {2, 4, 6} and Z = {0, 2, 4, 6, 8}

Which of the given sets can be considered as the universal set for the given sets X, Y and Z?
(i). {0, 1, 2, 3, 4, 5, 6}
(ii). Ø
(iii). {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv). {1, 2, 3, 4, 5, 6, 7, 8}

Solution:
(i) {0, 1, 2, 3, 4, 5, 6}

This contains:
→ All elements of X: 1, 3, 5
→ All elements of Y: 2, 4, 6
→ All elements of Z: 0, 2, 4, 6, but 8 is missing
Not a universal set (missing 8)

(ii) Ø

The empty set contains no elements, so it can’t be a universal set for any non-empty set.
Not a universal set

(iii) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

This contains all elements of X, Y, and Z
This is a valid universal set

(iv) {1, 2, 3, 4, 5, 6, 7, 8}

→ Contains X and Y
→ Contains most of Z, but missing 0
Not a universal set (missing 0)

Class 11 Maths NCERT Solutions Chapter 1 Sets Ex 1.4

Ex 1.4 Class 11 Maths Q.1: Find the union of each of the following pairs of sets:
(i). P = {1, 4, 6} and Q = {1, 3, 4}
(ii). X = {a, e, i, o, u} and Y = {x, y, z}
(iii). X = {x: x is a natural number and multiple of 3} and Y = {x: x is a natural number less than 6}
(iv). X = {x: x is a natural number and 1 < x ≤ 5} and Y = {x: x is a natural number and 5 < x < 10}
(v). X = {4, 5, 6} and Y = Φ

Solution:
(i) P = {1, 4, 6} and Q = {1, 3, 4}

P ∪ Q = {1, 3, 4, 6}

(ii) X = {a, e, i, o, u} and Y = {x, y, z}

X ∪ Y = {a, e, i, o, u, x, y, z}

(iii)

X = {x : x is a natural number and multiple of 3} = {3, 6, 9, 12, …}
Y = {x : x is a natural number less than 6} = {1, 2, 3, 4, 5}
X ∪ Y = {1, 2, 3, 4, 5, 6, 9, 12, …}
→ This is an infinite set: All natural numbers < 6 and all multiples of 3
X ∪ Y = {1, 2, 3, 4, 5, 6, 9, 12, 15, …}

(iv)

X = {x : x is a natural number and 1 < x ≤ 5} = {2, 3, 4, 5}
Y = {x : x is a natural number and 5 < x < 10} = {6, 7, 8, 9}
X ∪ Y = {2, 3, 4, 5, 6, 7, 8, 9}

(v) X = {4, 5, 6} and Y = Φ

X ∪ Y = {4, 5, 6}
(Since union with the empty set gives the set itself)

Ex 1.4 Class 11 Maths Q.2: Let A = {x, y} and B = {x, y, z}
Is A ⊂ B? What is A ∪ B?

Solution:
(i) Is A ⊂ B?

Yes,
→ A is a subset of B because all elements of A (x and y) are also in B.

So,
A ⊂ B is True

(ii) What is A ∪ B?

Union means all elements from both sets without repetition.

A ∪ B = {x, y} ∪ {x, y, z}
= {x, y, z}

Ex 1.4 Class 11 Maths Q.3: If X and Y are two sets such that X ⊂ Y, then what is X ∪ Y?

Solution:

Ex 1.4 Class 11 Maths Q.4: If P = {1, 2, 3, 4}, Q = {3, 4, 5, 6}, R = {5, 6, 7, 8} and S = {7, 8, 9, 10}
Find the following:
(i). P ∪ Q
(ii). P ∪ R
(iii). Q ∪ R
(iv). Q ∪ S
(v). P ∪ Q ∪ R
(vi). P ∪ Q ∪ S
(vii). Q ∪ R ∪ S

Solution:
(i) P ∪ Q

= {1, 2, 3, 4} ∪ {3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}

(ii) P ∪ R

= {1, 2, 3, 4} ∪ {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}

(iii) Q ∪ R

= {3, 4, 5, 6} ∪ {5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}

(iv) Q ∪ S

= {3, 4, 5, 6} ∪ {7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}

(v) P ∪ Q ∪ R

= {1, 2, 3, 4} ∪ {3, 4, 5, 6} ∪ {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}

(vi) P ∪ Q ∪ S

= {1, 2, 3, 4} ∪ {3, 4, 5, 6} ∪ {7, 8, 9, 10}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

(vii) Q ∪ R ∪ S

= {3, 4, 5, 6} ∪ {5, 6, 7, 8} ∪ {7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}

Ex 1.4 Class 11 Maths Q.5: Find the intersection of each of the following pairs of sets:
(i). P = {1, 4, 6} and Q = {1, 3, 4}
(ii). X = {a, e, i, o, u} and Y = {x, y, z}
(iii). X = {x: x is a natural number and multiple of 3} and Y = {x: x is a natural number less than 6}
(iv). X = {x: x is a natural number and 1 < x ≤ 5} and Y = {x: x is a natural number and 5 < x < 10}
(v). X = {4, 5, 6} and Y = Φ

Solution

(i) P = {1, 4, 6}
Q = {1, 3, 4}
P ∩ Q = {1, 4}

(ii) X = {a, e, i, o, u}
Y = {x, y, z}
X ∩ Y = Φ (no common elements)

(iii)
X = {x: x is a natural number and multiple of 3} = {3, 6, 9, 12, …}
Y = {x: x is a natural number less than 6} = {1, 2, 3, 4, 5}
X ∩ Y = {3}

(iv)
X = {x: x is a natural number and 1 < x ≤ 5} = {2, 3, 4, 5}
Y = {x: x is a natural number and 5 < x < 10} = {6, 7, 8, 9}
X ∩ Y = Φ (no common elements)

(v)
X = {4, 5, 6}
Y = Φ (empty set)
X ∩ Y = Φ

Ex 1.4 Class 11 Maths Q.6: If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}
Find the following:
(i). A ∩ B
(ii). B ∩  C
(iii). A ∩  C ∩  D
(iv). A ∩  C
(v).   B ∩  D
(vi). A ∩  (B ∪ C)
(vii). A ∩  D
(viii). A ∩  (B ∪ D)
(ix). (A ∩  B) ∩  (B ∪ C)
(x). (A∪  D) ∩  (B ∪ C)

Solution:
(i). A ∩ B
Common elements in A and B = {7, 9, 11}

(ii). B ∩ C
Common elements in B and C = {11, 13}

(iii). A ∩ C ∩ D
A ∩ C = {11}
Now, {11} ∩ D = Φ

(iv). A ∩ C
Common elements in A and C = {11}

(v). B ∩ D
Common elements in B and D = Φ

(vi). A ∩ (B ∪ C)
First, B ∪ C = {7, 9, 11, 13, 15}
Now, A ∩ {7, 9, 11, 13, 15} = {7, 9, 11}

(vii). A ∩ D
Common elements in A and D = Φ

(viii). A ∩ (B ∪ D)
B ∪ D = {7, 9, 11, 13, 15, 17}
A ∩ {7, 9, 11, 13, 15, 17} = {7, 9, 11}

(ix). (A ∩ B) ∩ (B ∪ C)
A ∩ B = {7, 9, 11}
B ∪ C = {7, 9, 11, 13, 15}
Now, {7, 9, 11} ∩ {7, 9, 11, 13, 15} = {7, 9, 11}

(x). (A ∪ D) ∩ (B ∪ C)
A ∪ D = {3, 5, 7, 9, 11, 15, 17}
B ∪ C = {7, 9, 11, 13, 15}
Now, intersection = {7, 9, 11, 15}

Ex 1.4 Class 11 Maths Q.7: If A = {y: y is a natural number}, B ={y: y is an even natural number}, C = {y: y is an odd natural number} and D = {y: y is a prime number}
Find the following:
(i). A ∩ B
(ii). A ∩ C
(iii). A ∩ D
(iv). B ∩ C
(v). B ∩ D
(vi). C ∩ D

Solution :
(i) A ∩ B

→ Common elements in A and B = all even natural numbers
Answer: {2, 4, 6, 8, 10, …} = B

(ii) A ∩ C

→ Common elements in A and C = all odd natural numbers
Answer: {1, 3, 5, 7, 9, …} = C

(iii) A ∩ D

→ Common elements in A and D = all prime numbers (since primes are part of natural numbers)
Answer: {2, 3, 5, 7, 11, 13, …} = D

(iv) B ∩ C

→ Even ∩ Odd = No common element
Answer: Φ (null set)

(v) B ∩ D

→ Even numbers that are prime
Only even prime number = 2
Answer: {2}

(vi) C ∩ D

→ Odd numbers that are prime = All odd prime numbers
(excluding 2 which is the only even prime)
Answer: {3, 5, 7, 11, 13, …} (all odd primes)

Ex 1.4 Class 11 Maths Q.8: Which of the given pairs of sets are disjoint?
(i). A = {1, 2, 3, 4} and B = {x: x is a natural number and 4 ≤ x ≤ 6}
(ii). A = {a, e, i, o, u} and B = {c, d, e, f}
(iii). A = {x: x is an even integer} and B = {x: x is an odd integer}

Solution:
(i)

A = {1, 2, 3, 4}
B = {x: x is a natural number and 4 ≤ x ≤ 6} = {4, 5, 6}
→ Common element: 4
Not disjoint

(ii)

A = {a, e, i, o, u}
B = {c, d, e, f}
→ Common element: e
Not disjoint

(iii)

A = {x: x is an even integer} = {…, –4, –2, 0, 2, 4, …}
B = {x: x is an odd integer} = {…, –3, –1, 1, 3, 5, …}
→ No common elements between even and odd integers
Disjoint

Ex 1.4 Class 11 Maths Q.9: If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}
Find the following:
(i). A – B
(ii). A – C
(iii). A – D
(iv). B – A
(v). C – A
(vi). D – A
(vii). B – C
(viii). B – D
(ix). C – B
(x). D – B
(xi). C – D
(xii). D – C

Solution 9:
(i) A – B

Elements in A but not in B
= {3, 6, 9, 12, 15, 18, 21} – {4, 8, 12, 16, 20}
= {3, 6, 9, 15, 18, 21}

(ii) A – C

= A – C
= {3, 6, 9, 12, 15, 18, 21} – {2, 4, 6, 8, 10, 12, 14, 16}
= {3, 9, 15, 18, 21}

(iii) A – D

= {3, 6, 9, 12, 15, 18, 21} – {5, 10, 15, 20}
= {3, 6, 9, 12, 18, 21}

(iv) B – A

= {4, 8, 12, 16, 20} – {3, 6, 9, 12, 15, 18, 21}
= {4, 8, 16, 20}

(v) C – A

= {2, 4, 6, 8, 10, 12, 14, 16} – {3, 6, 9, 12, 15, 18, 21}
= {2, 4, 8, 10, 14, 16}

(vi) D – A

= {5, 10, 15, 20} – {3, 6, 9, 12, 15, 18, 21}
= {5, 10, 20}

(vii) B – C

= {4, 8, 12, 16, 20} – {2, 4, 6, 8, 10, 12, 14, 16}
= {20}

(viii) B – D

= {4, 8, 12, 16, 20} – {5, 10, 15, 20}
= {4, 8, 12, 16}

(ix) C – B

= {2, 4, 6, 8, 10, 12, 14, 16} – {4, 8, 12, 16, 20}
= {2, 6, 10, 14}

(x) D – B

= {5, 10, 15, 20} – {4, 8, 12, 16, 20}
= {5, 10, 15}

(xi) C – D

= {2, 4, 6, 8, 10, 12, 14, 16} – {5, 10, 15, 20}
= {2, 4, 6, 8, 12, 14, 16}

(xii) D – C

= {5, 10, 15, 20} – {2, 4, 6, 8, 10, 12, 14, 16}
= {5, 15, 20}

Ex 1.4 Class 11 Maths Q.10: If X = {a, b, c, d} and Y = {f, b, d, g}
Find the following:
(i). X – Y
(ii). Y – X
(iii). X ∩ Y

Solution:
i) X – Y

Elements in X but not in Y
= {a, b, c, d} – {b, d, f, g}
= {a, c}

(ii) Y – X

Elements in Y but not in X
= {f, b, d, g} – {a, b, c, d}
= {f, g}

(iii) X ∩ Y

Common elements in X and Y
= X ∩ Y = elements common to both
= {b, d}

Q.11: What is R – Q, if R is the set of real numbers and Q is the set of rational?

Solution:

R = Set of real numbers
Q = Set of rational numbers
R – Q = Set of real numbers that are not rational
= Set of irrational numbers

Answer:
R – Q = Set of irrational numbers

12.Examples include: √2, √3, π, e, etc.ther the following statements are true or false. Give reason.
(i). A = {2, 3, 4, 5} and B = {3, 6} are disjoint sets.
(ii). A = {a, e, i, o, u } and B = {a, b, c, d} are disjoint sets.
(iii). A = {2, 6, 10, 14} and B = {3, 7, 11, 15} are disjoint sets.
(iv). A = {2, 6, 10} and B = {3, 7, 11} are disjoint sets.

Solution:
(i) A = {2, 3, 4, 5} and B = {3, 6}

Common element(s): 3 is present in both A and B.
Conclusion: They are not disjoint.

False – Because the sets share the element 3.

(ii) A = {a, e, i, o, u} and B = {a, b, c, d}

Common element(s): ‘a’ is present in both A and B.
Conclusion: They are not disjoint.

False – Because the sets share the element ‘a’.

(iii) A = {2, 6, 10, 14} and B = {3, 7, 11, 15}

Common element(s): None.
Conclusion: They are disjoint.

True – Because they do not share any elements.

(iv) A = {2, 6, 10} and B = {3, 7, 11}

Common element(s): None.
Conclusion: They are disjoint.

True – Because they do not share any elements.

NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.5

Ex 1.5 Class 11 Maths Q.1: Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
X = {1, 2, 3, 4, 5}
Y = {2, 4, 6} and
Z = {2, 4, 5, 6}.
Find the following sets:
(i). X’
(ii). Y’
(iii). (X∪Y)′
(iv). (X∪Z)′
(v). (X′)‘
(vi). (Y–Z)′

Solution:
Given:

Universal set, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
X = {1, 2, 3, 4, 5}
Y = {2, 4, 6}
Z = {2, 4, 5, 6}

(i) X′
= U – X
= {6, 7, 8, 9}

(ii) Y′
= U – Y
= {1, 3, 5, 7, 8, 9}

(iii) (X ∪ Y)′
X ∪ Y = {1, 2, 3, 4, 5, 6}
(X ∪ Y)′ = U – (X ∪ Y)
= {7, 8, 9}

(iv) (X ∪ Z)′
X ∪ Z = {1, 2, 3, 4, 5, 6}
(X ∪ Z)′ = U – (X ∪ Z)
= {7, 8, 9}

(v) (X′)′
= X
= {1, 2, 3, 4, 5}

(vi) (Y – Z)′
Y – Z = {} (empty set)
(Y – Z)′ = U – {}
= {1, 2, 3, 4, 5, 6, 7, 8, 9}

Ex 1.5 Class 11 Maths Q.2: If U = {a, b, c, d, e, f, g, h}, find the complements of the given sets:
(i). W = {a, b, c}
(ii). X = {d, e, f, g}
(iii). Y = {a, c, e, g}
(iv). Z = {f, g, h, a}

Solution:
Universal set,
U = {a, b, c, d, e, f, g, h}

(i) W = {a, b, c}

W′ = U – W
= {d, e, f, g, h}

(ii) X = {d, e, f, g}

X′ = U – X
= {a, b, c, h}

(iii) Y = {a, c, e, g}

Y′ = U – Y
= {b, d, f, h}

(iv) Z = {f, g, h, a}

Z′ = U – Z
= {b, c, d, e}

Ex 1.5 Class 11 Maths Q.3: Take natural numbers as the universal set. Write the complements of the given sets:
(i). A = {y: y is an even natural number}
(ii). B = {y: y is an odd natural number}
(iii). C = {y: y is a positive multiple of 3}
(iv). D = {y: y is a prime number}
(v). E = {y: y is a natural number divisible by 3 and 5}
(vi). F = {y: y is a perfect square}
(vii). G = {y: y is perfect cube}
(viii). H = {y: y + 5 = 8}
(ix). I = {y: 2y + 5 = 9}
(x). J = {y: y ≥ 7}
(xi). K = {y: y ∈ N and 2y + 1 > 10}

Solution:
(i) A = {y: y is an even natural number}

A′ = All odd natural numbers
A′ = {1, 3, 5, 7, 9, 11, …}

(ii) B = {y: y is an odd natural number}

B′ = All even natural numbers
B′ = {2, 4, 6, 8, 10, 12, …}

(iii) C = {y: y is a positive multiple of 3}

C′ = All natural numbers not divisible by 3
C′ = {1, 2, 4, 5, 7, 8, 10, …}

(iv) D = {y: y is a prime number}

D′ = All natural numbers that are not prime
D′ = {1, 4, 6, 8, 9, 10, 12, …}

(v) E = {y: y is a natural number divisible by 3 and 5}

Multiples of 15
E = {15, 30, 45, 60, …}
E′ = N without multiples of 15
E′ = {1–14, 16–29, 31–44, …}

(vi) F = {y: y is a perfect square}

F = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …}
F′ = All natural numbers not perfect squares
F′ = {2, 3, 5, 6, 7, 8, 10, 11, …}

(vii) G = {y: y is a perfect cube}

G = {1, 8, 27, 64, 125, …}
G′ = Natural numbers that are not perfect cubes
G′ = {2–7, 9–26, 28–63, 65–124, …}

(viii) H = {y: y + 5 = 8}

Solve: y = 3
H = {3}
H′ = N without 3
H′ = {1, 2, 4, 5, 6, 7, …}

(ix) I = {y: 2y + 5 = 9}

Solve: 2y = 4 → y = 2
I = {2}
I′ = N without 2
I′ = {1, 3, 4, 5, 6, 7, …}

(x) J = {y: y ≥ 7}

J = {7, 8, 9, 10, …}
J′ = {1, 2, 3, 4, 5, 6}

(xi) K = {y ∈ N and 2y + 1 > 10}

Solve: 2y + 1 > 10
→ 2y > 9
→ y > 4.5
→ y ≥ 5 (since y ∈ N)
K = {5, 6, 7, 8, …}
K′ = {1, 2, 3, 4}

Ex 1.5 Class 11 Maths Q.4: If U = {1, 2, 3, 4, 5,6,7,8, 9}
A = {2, 4, 6, 8} and, B = {2, 3, 5, 7}.
Verify that:
(i). (A∪B)′ = A′∩B′
(ii). (A∩B)′ = A′∪B′

Solution:
(i) Verify: (A ∪ B)’ = A’ ∩ B’

Step 1:
A ∪ B = {2, 3, 4, 5, 6, 7, 8}

Step 2:
(A ∪ B)’ = U – (A ∪ B) = {1, 9}

Step 3:
A’ = U – A = {1, 3, 5, 7, 9}
B’ = U – B = {1, 4, 6, 8, 9}

Step 4:
A’ ∩ B’ = Common elements of A’ and B’ = {1, 9}

Result:
(A ∪ B)’ = {1, 9}
A’ ∩ B’ = {1, 9}
Verified

(ii) Verify: (A ∩ B)’ = A’ ∪ B’

Step 1:
A ∩ B = {2}

Step 2:
(A ∩ B)’ = U – {2} = {1, 3, 4, 5, 6, 7, 8, 9}

Step 3:
A’ = {1, 3, 5, 7, 9}
B’ = {1, 4, 6, 8, 9}

Step 4:
A’ ∪ B’ = {1, 3, 4, 5, 6, 7, 8, 9}

Result:
(A ∩ B)’ = {1, 3, 4, 5, 6, 7, 8, 9}
A’ ∪ B’ = {1, 3, 4, 5, 6, 7, 8, 9}
Verified

Ex 1.5 Class 11 Maths Q.5: Draw the Venn diagrams for the following:
(i). (A∪B)′
(ii). A′∩B′
(iii). (A∩B)′
(iv). A′∪B′

Solution: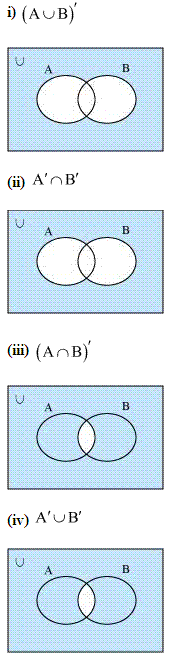
sets class 11 NCERT Solutions Ex 1.5 Q 5

Q.6: Let U be the universal set that is the set of all triangles in a plane. If X is the set of all triangles with at least one angle different from 60∘, what is X’ ?

Solution:
Given:

Universal set U = set of all triangles in a plane
Set X = set of all triangles with at least one angle different from 60°
We are asked to find X′, the complement of X.

Understanding X′ (the complement of X):

X′ = all elements in U that are not in X
In other words, X′ contains all triangles where none of the angles is different from 60°
That means all three angles must be 60°

X′ = {all equilateral triangles}

These are the only triangles where all angles are exactly 60°, so they do not belong to X (which includes all triangles with at least one angle different from 60°).

Q.7: Complete the given statements using proper symbols:
(i). A∪A′
(ii). Ø ∩A
(iii). A∩A′
(iv). U′∩A

Solution:
(i) A ∪ A′ = U

The union of a set and its complement is the universal set.
Answer: A ∪ A′ = U

(ii) Ø ∩ A = Ø

The intersection of the empty set with any set is always the empty set.
Answer: Ø ∩ A = Ø

(iii) A ∩ A′ = Ø

A set and its complement have no common elements, so their intersection is the empty set.
Answer: A ∩ A′ = Ø

(iv) U′ ∩ A = Ø

So, Ø ∩ A = Ø
Answer: U′ ∩ A = Ø

The complement of the universal set (U′) is the empty set.

NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.6

Ex 1.6 Class 11 Maths Q.1: If A and B are two sets such that n(A) = 16, n(B) = 24 and n(A∪B) = 39. Find n(A∩B).

Solution:

Given:
n(A) = 16
n(B) = 24
n(A ∪ B) = 39

We use the formula:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Substitute the values:
39 = 16 + 24 – n(A ∩ B)
39 = 40 – n(A ∩ B)

So,
n(A ∩ B) = 40 – 39 = 1

Q.2: If A and B are two sets such that A∪B has 17 elements, A has 9 elements and B has 14 elements. How many elements does A∩B have?

Solution:
Given:
n(A ∪ B) = 17
n(A) = 9
n(B) = 14

Formula:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Substitute values:
17 = 9 + 14 – n(A ∩ B)
17 = 23 – n(A ∩ B)

So,
n(A ∩ B) = 23 – 17 = 6

Q.3: In a group there are 450 people, 200 speaks Hindi and 270 can speak English. How many people can speak Ex both English and Hindi?

Solution:
Given:
Total people = 450
People who speak Hindi = 200
People who speak English = 270

Let the number of people who speak both Hindi and English = n(H ∩ E)

Using the formula:
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)

Since total people = 450, and everyone is counted at least once in Hindi or English speakers or both, we assume:
n(H ∪ E) ≤ 450

To find n(H ∩ E), we use:
n(H ∪ E) = total people = 450 (assuming everyone speaks at least one language)

So,
450 = 200 + 270 – n(H ∩ E)
450 = 470 – n(H ∩ E)

Therefore,
n(H ∩ E) = 470 – 450 = 20

Ex 1.6 Class 11 Maths Q.4: If X and Y are two sets such that X has 22 elements, Y has 34 elements, and n(X∩Y) has 10 elements, how many elements does n(X∪Y) have?

Solution:
Given:
n(X) = 22
n(Y) = 34
n(X ∩ Y) = 10

Formula:
n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)

n(X ∪ Y) = 22 + 34 – 10
n(X ∪ Y) = 56

Ex 1.6 Class 11 Maths Q.5: If A and B are two sets such that A has 45 elements, n (A ∩ B) has 15 elements and n (A ∪ B) has 70 elements, how many elements does B have?

Solution:
Given:
n(A) = 45
n(A ∩ B) = 15
n(A ∪ B) = 70

Formula:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Substitute values:
70 = 45 + n(B) – 15

70 = 30 + n(B)

Solve for n(B):
n(B) = 70 – 30 = 40

Ex 1.6 Class 11 Maths Q.6:There are 70 people, out of which 35 like tea, 55 like coffee, and each person likes at least one of the two beverages. How many people like both tea and coffee?

Solution:
Total people = 70
People who like tea = 35
People who like coffee = 55
Each person likes at least one of the two beverages.

Let:
Number of people who like both tea and coffee = n(T ∩ C)

Formula:
n(T ∪ C) = n(T) + n(C) – n(T ∩ C)

Since everyone likes at least one beverage,
n(T ∪ C) = 70

Substitute values:
70 = 35 + 55 – n(T ∩ C)
70 = 90 – n(T ∩ C)

Solve for n(T ∩ C):
n(T ∩ C) = 90 – 70 = 20

Ex 1.6 Class 11 Maths Q.7: There are 70 students in a group, 35 like cricket, 15 like both tennis and cricket. How many like tennis only and not cricket? How many like tennis?

Solution:
Given:
Total students = 70
Students who like cricket = 35
Students who like both tennis and cricket = 15

Let:

Number of students who like tennis only (not cricket) = x
Total students who like tennis = T = tennis only + both tennis and cricket = x + 15

Since we don’t know how many students like tennis in total or only tennis, we can’t find exact numbers without more info.

But if we assume everyone likes at least one of the two games (cricket or tennis), then:

Total students = Students who like cricket only + Students who like tennis only + Students who like both

Let cricket only = 35 – 15 = 20 (because 15 like both cricket and tennis)
Let tennis only = x
Both = 15

So,
20 + x + 15 = 70
x + 35 = 70
x = 70 – 35 = 35

Therefore:

Total students who like tennis = tennis only + both = 35 + 15 = 50

Number of students who like tennis only = 35

Q.8: In a committee, 60 people speak French, 30 speak Spanish and 20 speak both Spanish and French. How many speak at least one of these two languages?

Solution:
Given:
People who speak French = 60
People who speak Spanish = 30
People who speak both French and Spanish = 20

Let:
Number of people who speak at least one language = n(F ∪ S)

Formula:
n(F ∪ S) = n(F) + n(S) – n(F ∩ S)

n(F ∪ S) = 60 + 30 – 20
n(F ∪ S) = 70

CLASS 11 Biology SOLUTIONS