Class 11 Physics Gravitation is arguably one of the most fundamental and pervasive forces in the universe. Early in our lives, we become acutely aware of the tendency of all material objects to be attracted towards the Earth. Whether it’s a ball thrown upward falling back down, raindrops streaming from the clouds, or the simple effort required to walk uphill—all these everyday phenomena are manifestations of this unseen force.
Historically, the study of gravity was a crucial step in the development of modern physics. It was the brilliant Italian physicist Galileo Galilei (1564-1642) who first recognized that all bodies, regardless of their mass, accelerate towards the Earth at a constant rate.
However, the complete understanding of gravitation required linking terrestrial phenomena with celestial motion. Observations of the stars, planets, and their intricate movements had captivated astronomers for millennia.
The pivotal breakthrough came with the work of Johannes Kepler and later, Sir Isaac Newton, who provided the mathematical framework that successfully described both an apple falling from a tree and the orbit of the Moon around the Earth.

In this chapter, we will embark on a journey from the simple kinematics of falling bodies to the grand mechanics of the solar system. We will explore Kepler’s Laws, formulate Newton’s Universal Law of Gravitation, and delve into key concepts like acceleration due to gravity, gravitational potential energy, and the critical mechanics governing Earth satellites.
Kepler’s Laws
The motion of planets had been a subject of great fascination and study for thousands of years. Early models of the solar system, such as those proposed by Claudius Ptolemy, were geocentric (Earth-centered). The significant shift to the heliocentric (Sun-centered) model was championed by Nicolaus Copernicus (1473-1543).
However, it was the meticulous astronomical observations gathered by Tycho Brahe (1546-1601) that allowed his successor, Johannes Kepler (1571-1630), to formulate three fundamental laws of planetary motion.
Kepler’s laws describe the motion of planets in the solar system.
Law I: Law of Orbits
All planets move in elliptical orbits with the Sun situated at one of the foci.
This law refuted the ancient idea that planetary orbits must be perfectly circular. An ellipse has two focal points, and the Sun sits at one of them. The distance from the Sun to the planet is not constant; it changes as the planet moves through its orbit.
Law II: Law of Areas
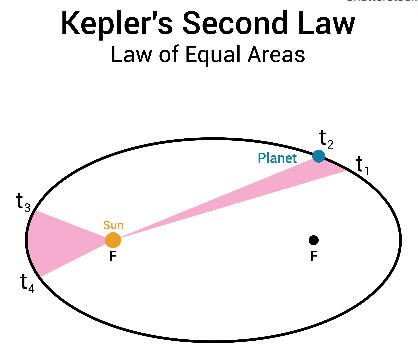
The line that joins any planet to the Sun sweeps out equal areas in equal intervals of time.
This law is a consequence of the conservation of angular momentum. Since the planet-Sun line sweeps out equal areas in equal times, the planet must move faster when it is closer to the Sun (at the perihelion) and slower when it is farther away (at the aphelion).
Law III: Law of Periods
The square of the time period of revolution (T^2) of any planet around the Sun is directly proportional to the cube of the semi-major axis (R^3) of its elliptical orbit. Mathematically:
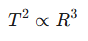
This law shows that the farther a planet is from the Sun (larger R), the longer its orbital period (T) will be. This relationship holds true for all planets orbiting the Sun and for any set of satellites orbiting a central body. Kepler’s third law provided crucial evidence for Newton to formulate the inverse-square nature of the gravitational force.
Class 11 Physics Gravitation – Exercises Solve
7.1 You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of a nearby body by putting it inside a hollow sphere or by some other means?
Ans: No, a body cannot be shielded from the gravitational influence of another body by placing it inside a hollow sphere or by any other method.
Unlike electric forces, gravity is always attractive and cannot be cancelled because there are no negative masses.
Although a hollow spherical shell exerts no net force on a body placed inside it, it cannot block or shield the gravitational effect of external bodies.
7.2 An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station is too small to create a detectable gravitational field, what is the cause of the gravity that he cannot detect?
Ans: The astronaut and the spaceship are both in free fall towards the Earth due to Earth’s gravity.
Since they fall with the same acceleration, the astronaut experiences weightlessness and cannot detect gravity inside the spaceship.
Thus, the cause of the gravity he cannot detect is Earth’s gravitational pull, but it is not felt because both the astronaut and the spaceship are accelerating together under its influence.
7.3 Select the correct alternative: (a) Acceleration due to gravity is always directed towards the centre of the earth/is directed towards the point where the mass is concentrated/is zero/is maximum at the equator.
(b) The gravitational force between a hollow spherical shell of uniform density and a point mass outside is the same as if the entire mass is concentrated at the centre of the shell/is zero/depends on the position of the point mass.
(c) The change in gravitational potential energy is defined as the work done by the gravitational force in taking the mass from initial point to final point/work done by external force in taking the mass from initial point to final point/negative of the work done by the gravitational force in taking the mass from initial point to final point.
(d) Gravitational potential energy of a two particle system is positive/negative/zero.
7.4 State true or false: (a) The escape velocity of a body from the surface of the earth is dependent on the mass of the body. (b) The escape velocity of a body from the surface of the earth is dependent on the direction of projection. (c) The escape velocity of a body from the surface of the earth is dependent on the height from which it is projected. (d) The escape velocity of a body from the surface of the earth is dependent on the rotation of the earth.
Ans: The astronaut and the spaceship are both in free fall towards the Earth due to Earth’s gravity.
Since they fall with the same acceleration, the astronaut experiences weightlessness and cannot detect gravity inside the spaceship.
Thus, the cause of the gravity he cannot detect is Earth’s gravitational pull, but it is not felt because both the astronaut and the spaceship are accelerating together under its influence.
7.5 State true or false: (a) The time period of a satellite in a circular orbit depends on the radius of its orbit. (b) The total energy of an orbiting satellite is always conserved. (c) The mechanical energy of an orbiting satellite is negative. (d) The potential energy of an orbiting satellite is positive.
Ans: (a) True – The time period of a satellite in circular orbit depends on the radius of its orbit (T2∝r3) (b) True – The total (mechanical) energy of an orbiting satellite remains conserved. (c) True – The mechanical energy of an orbiting satellite is negative (since it is bound to Earth’s gravitational field). (d) False – The potential energy of an orbiting satellite is negative, not positive.
7.6 An object weighs 10 N at the north pole of the earth. In a geostationary satellite, what is its true weight?
Ans: In a geostationary satellite, the object and the satellite both revolve around the Earth with the same angular velocity.
They are in a state of free fall under Earth’s gravity, so the object exerts no force on the supporting surface. Hence, its apparent (true) weight = 0 N.
7.7 What is the gravitational potential energy of a two particle system separated by a distance r?
Ans: The gravitational potential energy (U) of a two-particle system separated by a distance r is given by: U = – G m1 m2 / r where
G = universal gravitational constant,
m1 and m2 = masses of the two particles,
r = distance between them.
7.8 What is the gravitational potential at a distance r from the centre of the earth?
Ans: The gravitational potential (V) at a distance r from the centre of the Earth is given by: V = – G M / r where
G = universal gravitational constant,
M = mass of the Earth,
r = distance from the centre of the Earth
7.9 Calculate the escape speed for a satellite from the surface of the earth.
Ans: The escape speed (ve) of a satellite from the surface of the Earth is given by the formula: ve = √(2 G M / R) where
G = universal gravitational constant,
M = mass of the Earth,
R = radius of the Earth. For Earth,
ve = √(2 × 6.67 × 10⁻¹¹ × 5.97 × 10²⁴ / 6.37 × 10⁶)
≈ 1.12 × 10⁴ m/s
7.10 At what height above the earth’s surface is the acceleration due to gravity 1/4th of its value on the surface?
Ans: We know the formula for gravity at height h: g′ = g (R / (R + h))² Here,
g′ = new gravity,
g = gravity on Earth’s surface,
R = radius of Earth. Given that g′ = g / 4, So,
g / 4 = g (R / (R + h))²
1 / 4 = (R / (R + h))²
1 / 2 = R / (R + h)
R + h = 2R
h = R The height where gravity becomes one-fourth of its surface value is equal to the radius of the Earth,
that is h = 6.4 × 10⁶ m (or 6400 km) above the Earth’s surface.
7.11 Find the total mechanical energy of a satellite of mass 1000 kg orbiting at a height of 400 km above the earth’s surface. Mass of earth =6.0×1024 kg, Radius of earth =6.4×106 m.
Ans:
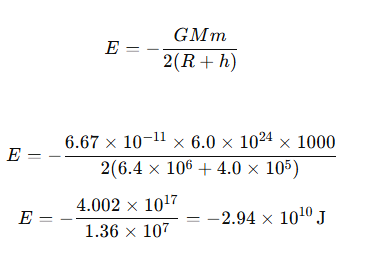
7.12 A satellite of mass 200 kg is lifted to a height of 600 km above the earth’s surface. Find the work done in lifting the satellite.
Ans:

7.13 A geostationary satellite orbits the earth at a height of 35,800 km. Find the time period of a satellite orbiting at a height of 400 km.
Ans:

7.14 The kinetic energy of an artificial satellite is: 1/2 of its potential energy/1/2 of its total energy/equal to its total energy/negative of its total energy.
Ans:
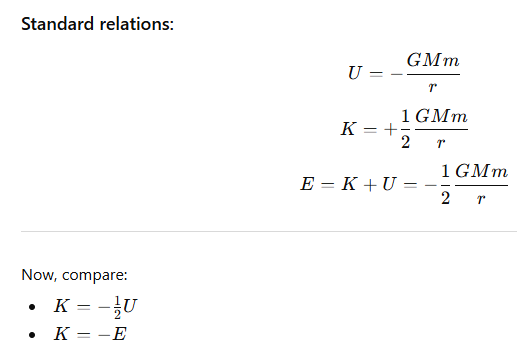
7.15 How will you weigh the sun?
Ans:

7.16 A body weighs 200 N on the surface of the earth. How much will it weigh half way down to the centre of the earth?
Ans:

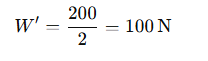
7.17 A rocket is fired vertically with a speed of 5 km / s from the earth’s surface. How far from the earth does the rocket go before returning to the earth? Mass of the earth =6.0×1024 kg; mean radius of the earth =6.4×106 m; G=6.67×10−11 N m^2 kg^{-2}
Ans:
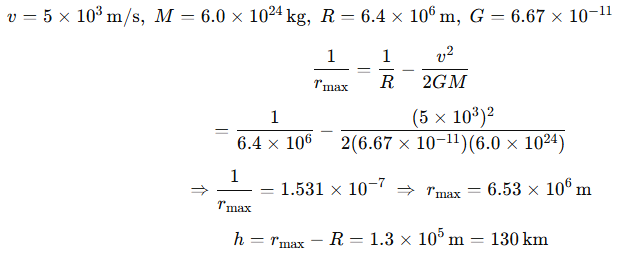
7.18 The escape speed of a projectile on the earth’s surface is 11.2 km /s . A body is projected out with thrice this speed. What is the speed of the body far away from the earth? Ignore the presence of the sun and other planets.
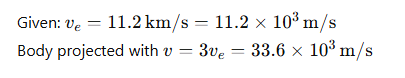
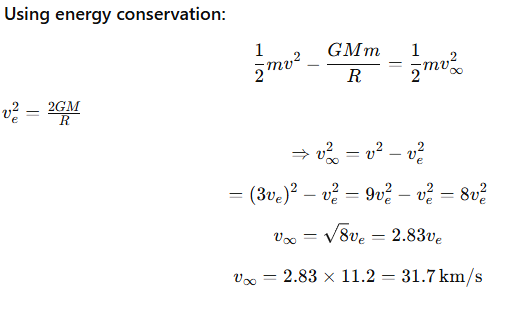
7.19 A satellite orbits the earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out of the earth’s gravitational influence? Mass of the satellite =200 kg; mass of the earth =6.0×1024 kg; radius of the earth =6.4×106 m; G=6.67×10−11 N m^2 kg^{-2}
Ans:
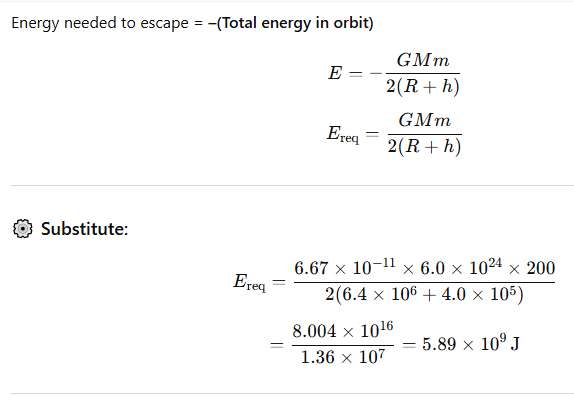
7.20 Two stars each of one solar mass (=2×1030 kg) are approaching each other for a head on collision. When they are a distance 109 km, their speeds are negligible. What is the speed with which they collide? The radius of each star is 104 km. Assume the stars to remain undistorted until they collide. (Use the known value…

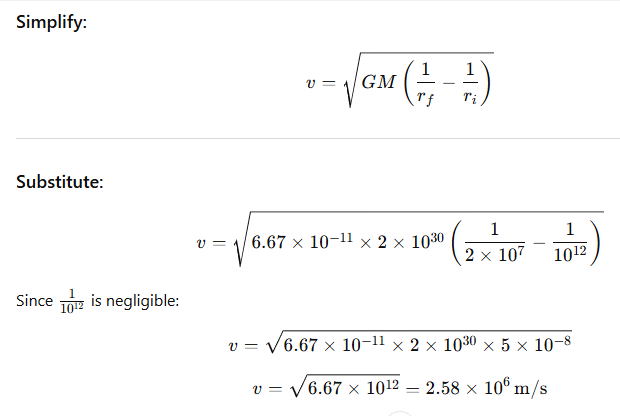
For the official Class 11 Physics Gravitation, you can visit:
- NCERT Textbooks (for Class 11):
Class-wise Solutions
Class 12:
Class 11:
- Class 11 Physics – NCERT Solutions
- Class 11 Chemistry – NCERT Solutions
- Class 11 Biology – NCERT Solutions
- Class 11 Math – NCERT Solutions
Class 10:
Class 9:
Class 8:
Class 7:
Class 6:
Subject-wise Solutions
Physics:
Chemistry:
Biology:
Math:
- Class 11 Math – NCERT Solutions
- Class 10 Math – NCERT Solutions
- Class 9 Math – NCERT Solutions
- Class 8 Math – NCERT Solutions
Science:
- Class 10 Science – NCERT Solutions
- Class 9 Science – NCERT Solutions
- Class 8 Science – Oxford Solutions
- Class 7 Science – Oxford Solutions
- Class 6 Science – Oxford Solutions
