The chapter System of Particles and Rotational Motion is an important part of Class 11 Physics (NCERT / CBSE syllabus) and is also studied as part of Grade 11 / High School Physics worldwide.

In this chapter, we extend the study of mechanics from individual particles to systems of particles and rigid bodies. It introduces key concepts such as the centre of mass, torque, angular momentum, equilibrium of rigid bodies, rotational dynamics, and moment of inertia.
These concepts are not only important for Class 11 exams but also form the foundation for Class 12 Physics, JEE, and NEET.
Class 11 System of Particles and Rotational Motion (NCERT / Grade 11)
Centre of Mass (COM)
The Centre of Mass (COM) of a system of particles is the point that represents the average position of the entire mass of the system. When analyzing motion, it is often easier to study the motion of the COM instead of dealing with each particle separately.
Every system of particles, no matter how complex, behaves as if all its mass were concentrated at the COM and all external forces acted at that point.
2. Definition
The centre of mass of a body or system of particles is defined as:
“The point at which the whole mass of the system may be considered to be concentrated, and about which the motion of the system can be described under the action of external forces.”
3. Mathematical Expression
3.1 For a System of Discrete Particles
For particles of masses m₁, m₂, m₃, … at position vectors r₁, r₂, r₃, …
Position vector of COM (R):
R = (m₁r₁ + m₂r₂ + m₃r₃ + …) / (m₁ + m₂ + m₃ + …)
In Cartesian coordinates:
- x-coordinate of COM:
x_com = (m₁x₁ + m₂x₂ + m₃x₃ + …) / (m₁ + m₂ + m₃ + …) - y-coordinate of COM:
y_com = (m₁y₁ + m₂y₂ + m₃y₃ + …) / (m₁ + m₂ + m₃ + …) - z-coordinate of COM:
z_com = (m₁z₁ + m₂z₂ + m₃z₃ + …) / (m₁ + m₂ + m₃ + …)
3.2 For a Continuous Body
If mass is distributed continuously, then:
R = (1/M) ∫ r dm
where M is total mass of the body and integration is over the entire volume.
4. Properties of COM
- The COM moves as if all external forces act on it.
- Internal forces do not affect the motion of COM (Newton’s third law).
- For symmetric bodies of uniform density, COM lies at the geometrical centre.
- Sphere: Centre of sphere.
- Cube: Geometrical centre.
- Rod (uniform): Midpoint.
- Ring: Centre of ring.
- COM may lie outside the body (e.g., hollow ring, boomerang).
5. Motion of COM
If a system of particles has total external force F_ext, then:
M (d²R/dt²) = F_ext
This shows the COM obeys Newton’s second law. The entire system behaves as if mass M were concentrated at COM.
6. Special Cases
6.1 Two-Particle System
If two masses m₁ and m₂ are placed on x-axis at positions x₁ and x₂:
x_com = (m₁x₁ + m₂x₂) / (m₁ + m₂)
The COM lies closer to the heavier mass.
6.2 Symmetrical Bodies of Uniform Density
- For a uniform rod, COM is at its midpoint.
- For a uniform sphere, COM is at the centre.
- For a uniform ring or disc, COM is at the centre.
7. Applications of COM
- Projectile motion of a body: A rotating projectile (like a thrown hammer) follows a parabolic path traced by its COM.
- Rocket motion: COM shifts as fuel is consumed.
- Stability of objects: Lower COM increases stability (e.g., racing cars).
- Astronomy: Earth-Moon system rotates about their common COM.
- Sports: Athletes shift their COM to optimize performance (e.g., high jump).
Linear Momentum in a System
- Linear momentum (p) = m × v
- For a system of particles, total momentum is the vector sum of all particles.
- Law of Conservation of Momentum: Total momentum remains constant if no external force acts.
Torque and Angular Momentum
- Torque (τ) = r × F
- Angular Momentum (L) = r × p
- Relation: τ = dL/dt
- Conservation of Angular Momentum: If no external torque acts, angular momentum remains conserved.
Equilibrium of Rigid Bodies
A rigid body is in equilibrium when:
- ΣF = 0 → No net force (translational equilibrium)
- Στ = 0 → No net torque (rotational equilibrium)
Rotational Dynamics
Newton’s second law for rotation:
τ = I × α
Where τ = torque, I = moment of inertia, α = angular acceleration
Moment of Inertia (MI) and Radius of Gyration
- MI measures resistance to change in rotational motion.
- I = Σ mi ri²
- Radius of gyration: K = √(I/M)
Standard values of MI (no derivations required):
- Uniform rod (about centre) = (1/12) ML²
- Uniform rod (about end) = (1/3) ML²
- Circular ring (about diameter) = (1/2) MR²
- Disc (about diameter) = (1/4) MR²
- Solid sphere (about diameter) = (2/5) MR²
- Hollow sphere = (2/3) MR²
Formula Summary
- COM (2-particle system): xcm = (m1x1 + m2x2) / (m1 + m2)
- Momentum: p = mv
- Torque: τ = r × F
- Angular Momentum: L = r × p
- Rotational Law: τ = Iα
- Radius of Gyration: K = √(I/M)
NCERT Exercise Solutions
Exercise 7.1 (Class 11 System of Particles and Rotational Motion)
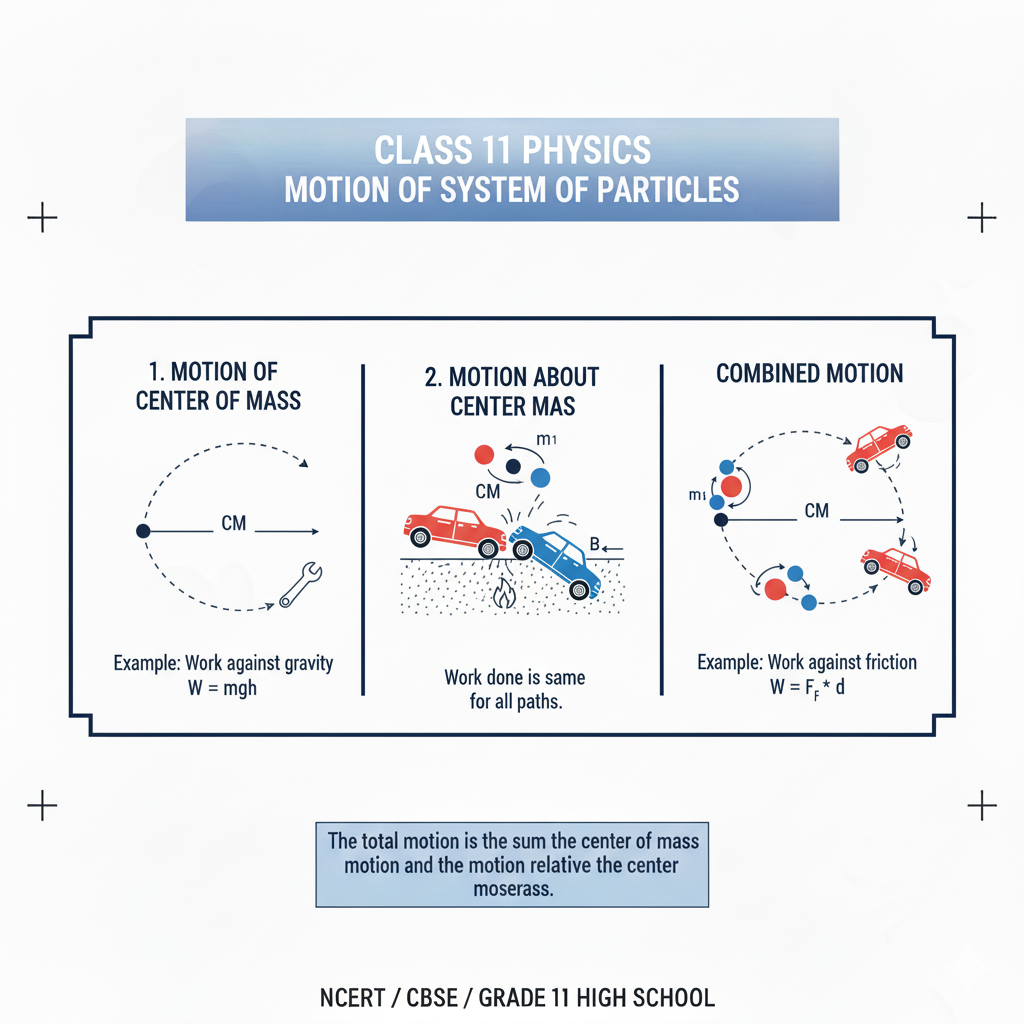
1.Show that the motion of a system of particles can be separated into motion of the centre of mass and motion about the centre of mass.
Consider a system of N particles. Let the i-th particle have mass mi and position vector ri(t) (measured from a fixed inertial origin). Define the total mass
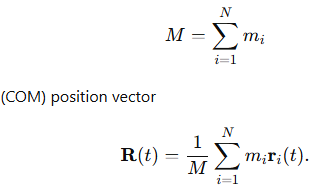
Now write the position of each particle as the sum of the COM position and the position relative to the COM:
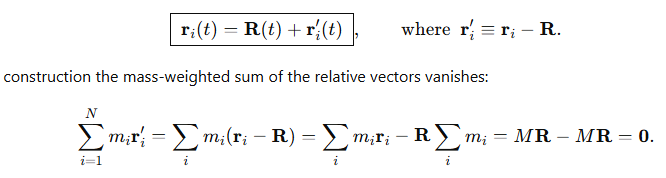

Thus the total momentum equals the momentum of a single particle of mass M located at the COM and moving with V. This shows the translational motion of the whole system is captured by motion of the COM.

Interpretation: the total kinetic energy equals the kinetic energy of the whole mass M moving with the COM velocity (pure translation) plus the kinetic energy of motion relative to the COM (internal or “internal” kinetic energy — rotation, vibrations, etc.).



2. Give the location of the centre of mass of the following uniform, symmetric bodies: i) a sphere ii) a cylinder iiii) a ring iv) a cube
Also, answer: Does the centre of mass of a body necessarily lie inside the body?
Ans:
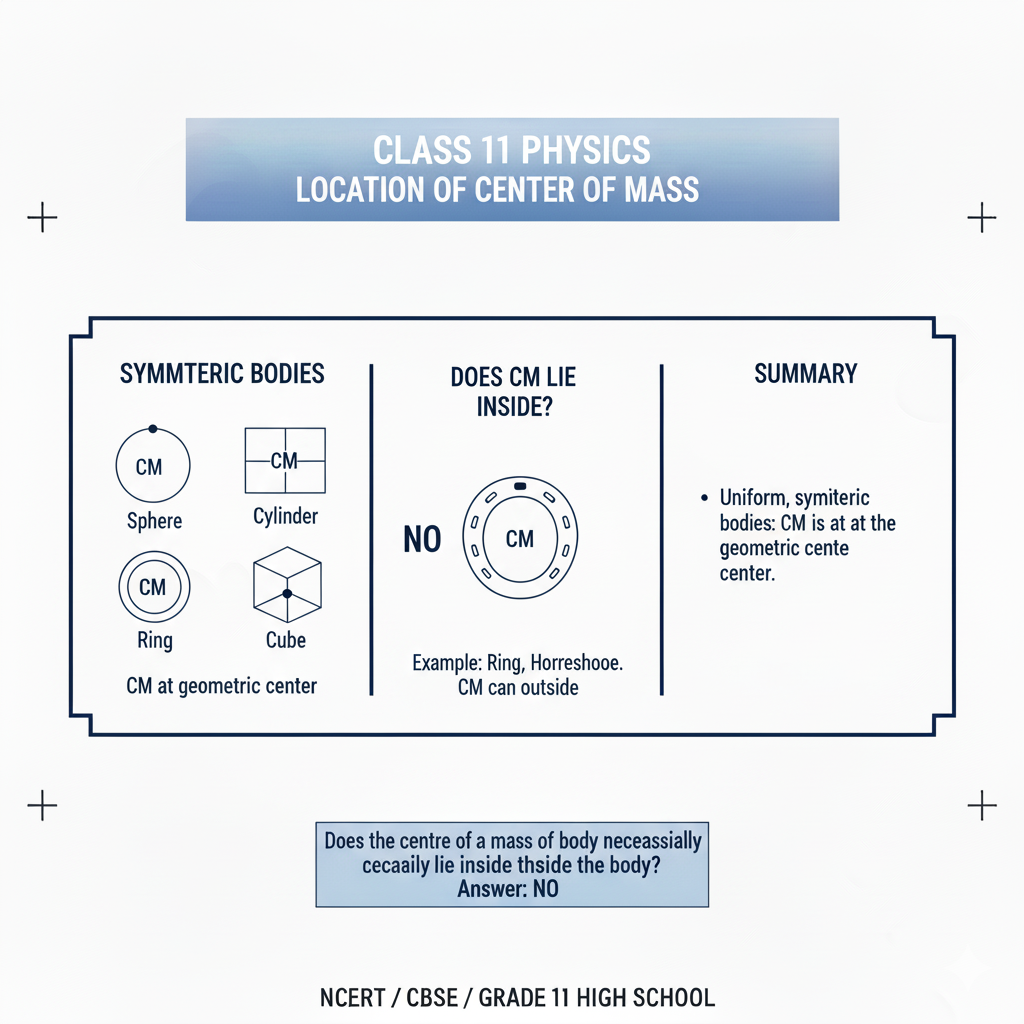
Location of the centre of mass (COM) for common uniform, symmetric bodies
i) Sphere (solid, uniform)
The COM is at the geometric centre of the sphere — the centre point equidistant from every point on the surface.
Reason: perfect spherical symmetry → every direction equivalent, so the only possible unique point is the centre.
ii) Cylinder (uniform, right circular)
The COM is on the axis of the cylinder at the midpoint of its height (i.e. halfway between the two circular faces).
Reason: symmetry about the axis and top/bottom; mass distribution is uniform along the axis so centre lies at mid-height on the central axis.
iii) Ring (thin circular ring / hoop, uniform)
The COM is at the centre of the circle (the geometric centre).
Note: for a thin ring this point is in the empty space at the middle of the ring (not in the material itself). The COM coincides with the centre of symmetry of the ring.
iv) Cube (uniform)
The COM is at the geometric centre of the cube — the intersection point of its body diagonals (midpoint of length, width and height).
Reason: translational symmetry along x, y, z directions; the only symmetric point is the centre.
Does the centre of mass necessarily lie inside the body?
No — not necessarily.
So the COM always lies inside the convex hull of the body, but need not lie within the material itself.
For solid, convex, homogeneous bodies (sphere, solid cube, solid cylinder, solid cone, etc.) the COM lies inside the material.
However, for hollow or non-convex objects the COM can lie outside the material. Examples:
A thin ring or hollow circular hoop: COM is at the circle centre, which is empty space.
A C-shaped or boomerang-shaped plate: COM may be outside the actual material.
3. In the HCl molecule, the distance between nuclei is approximately 1.27 Å. Find the approximate location of the centre of mass, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom.
Ans: Let the hydrogen nucleus be at position zero. The chlorine nucleus is at position 1.27 angstrom away from hydrogen.
Let the mass of hydrogen be 1 unit. Then the mass of chlorine is 35.5 units.
The position of the centre of mass is given by:
(mass of hydrogen × position of hydrogen + mass of chlorine × position of chlorine) ÷ (total mass).
Substituting values:
= (1 × 0 + 35.5 × 1.27) ÷ (1 + 35.5)
= (45.085) ÷ (36.5)
≈ 1.24 angstrom
Therefore, the centre of mass lies about 1.24 angstrom from the hydrogen atom, which is very close to the chlorine atom.
Distance of centre of mass from chlorine nucleus = 1.27 − 1.24 = 0.03 angstrom (approximately).
4. A child sits at one end of a trolley moving uniformly with speed V on a frictionless floor. If the child moves inside the trolley in any manner, what is the speed of the centre of mass of the system (trolley + child)?
Ans:

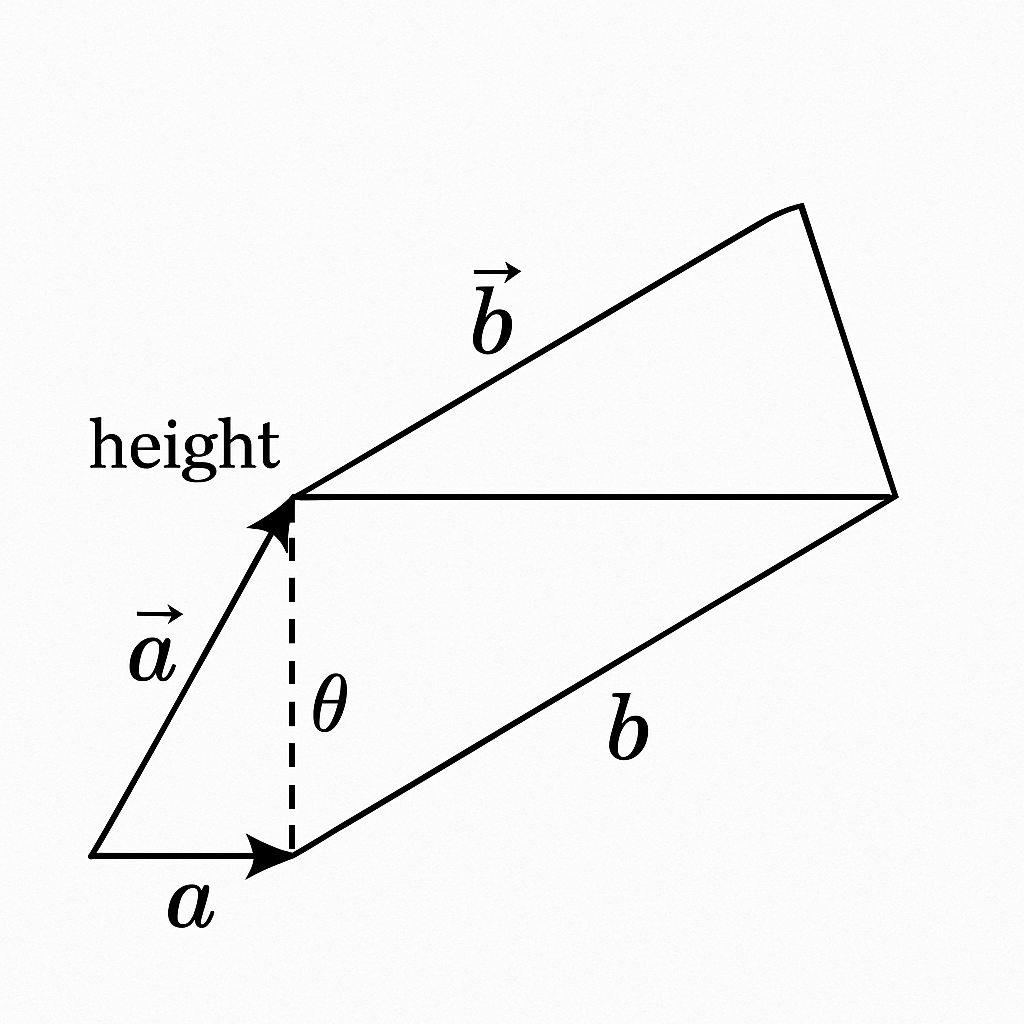
5. Show that the area of the triangle formed by vectors a and b is (1/2) |a × b|.
Ans:



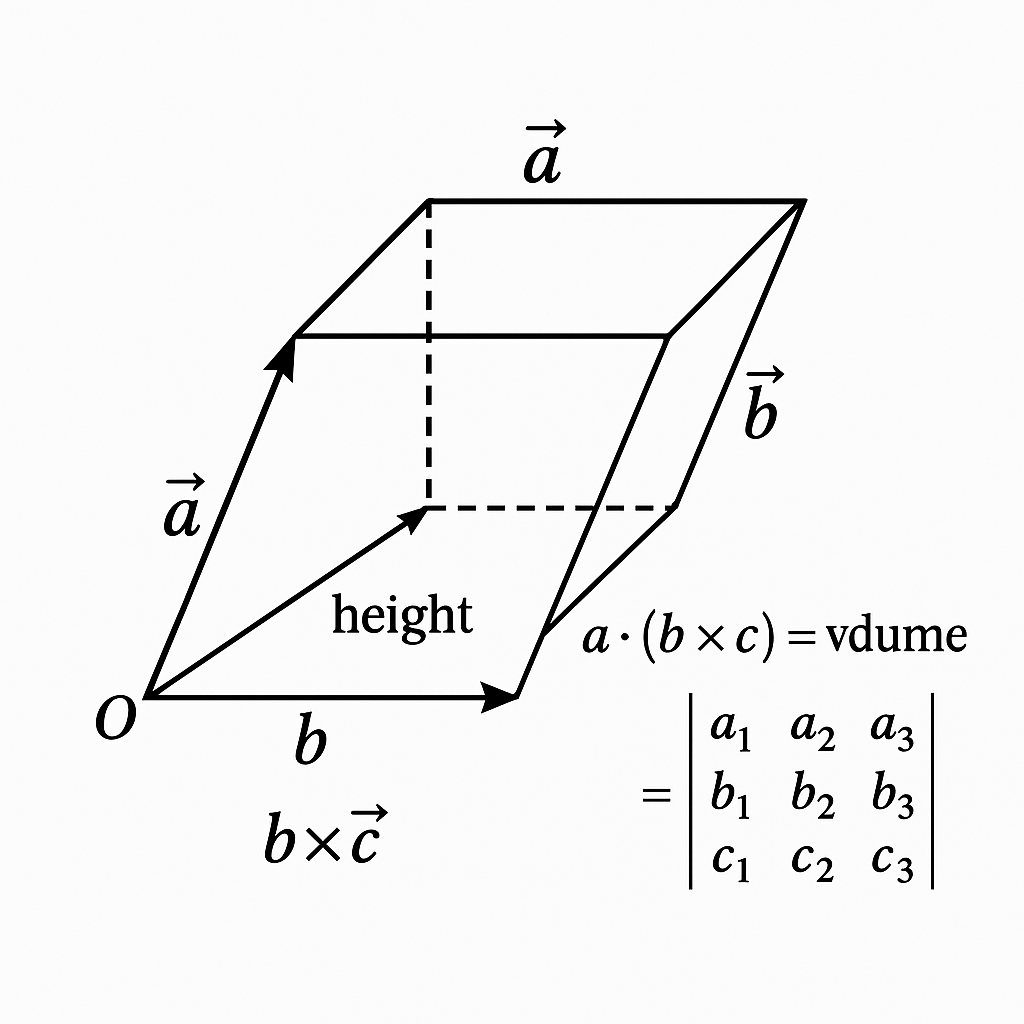
6. Show that a·(b × c) equals the volume of the parallelepiped formed by vectors a, b, and c.
Ans:




7. For a particle with position vector r = (x, y, z) and momentum p = (pₓ, p_y, p_z), find the components of angular momentum L. Also show that if the motion is confined to the xy-plane, L has only a z-component.
Ans:
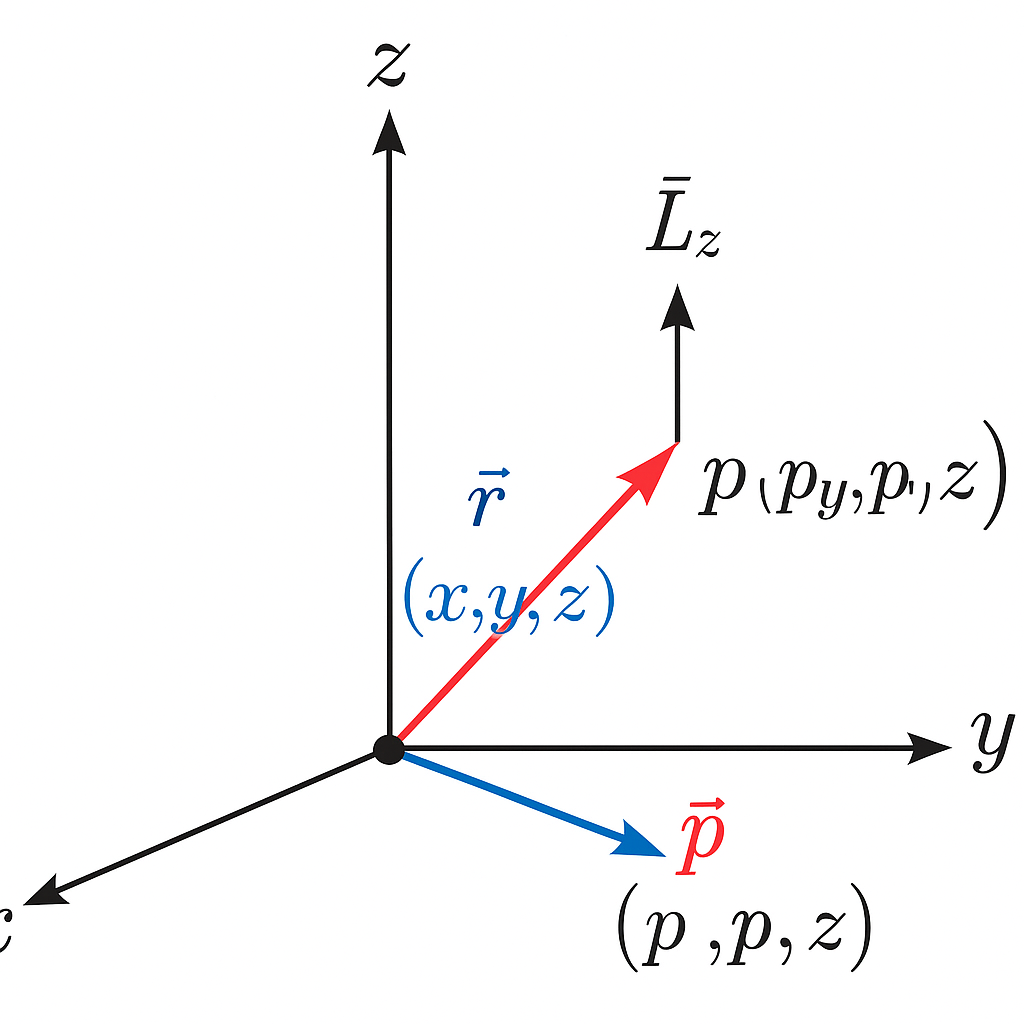
Angular momentum is defined as L=r×p
Using the determinant form of the cross product,
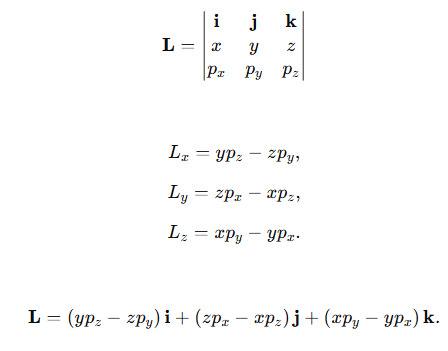

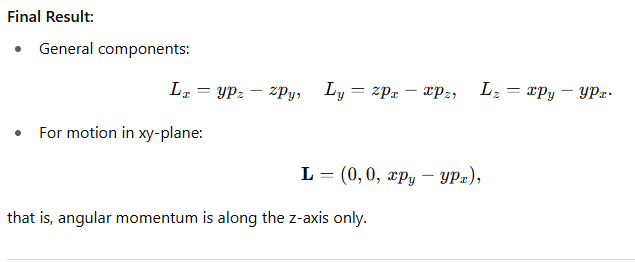
8. Two equal masses travel in opposite directions along parallel lines, separated by distance d. Prove that the vector angular momentum of the system is the same irrespective of the point about which it’s taken.
Ans:
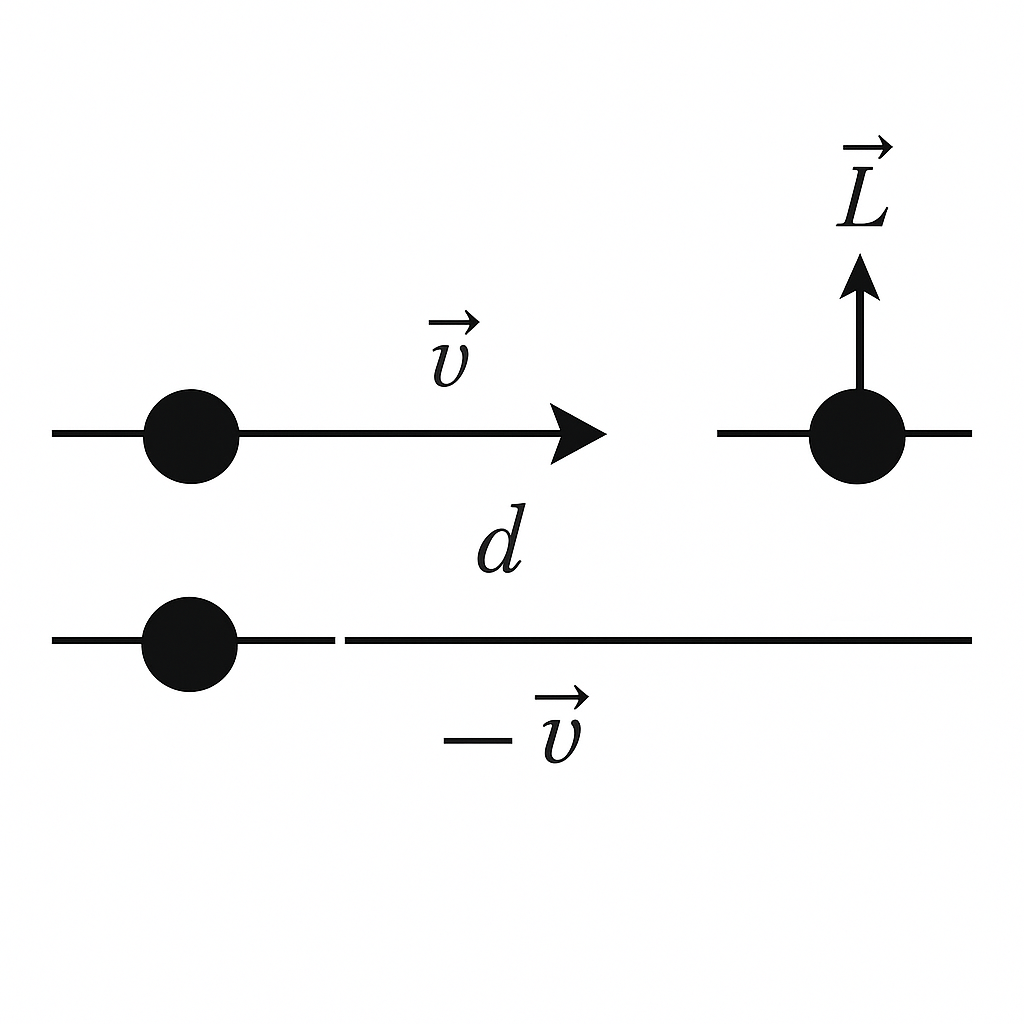
Let each mass be m
Let their velocities be equal in magnitude but opposite in direction: one moves with velocity v, the other with velocity −v.
The two parallel lines of motion are separated by a distance d
Step 1: Angular momentum of a particle about a point
For one particle: L=r×p=r×(mv)
where r is the position vector of the particle relative to the chosen point.
Step 2: System angular momentum
For two particles:
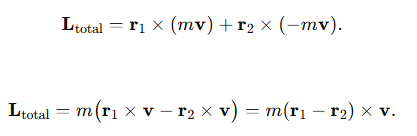
Step 3: Relative position
The difference r1−r2 is a vector of length d, perpendicular to v, pointing from one line of motion to the other.
Thus, Ltotal=m d×v
Here d is the displacement vector between the parallel lines, of magnitude d, and perpendicular to velocity v.
Step 4: Independence from origin
Notice that the result depends only on the separation vector d between the two lines of motion and the velocity v. It does not depend on the choice of reference point (origin).
Therefore, the angular momentum of the system is the same about any point.
Final Result:
The total angular momentum of the system is L=m (d×v)
which is independent of the origin chosen.
9. A plank of weight W is 2 m long and is suspended by two strings making angles 36.9° and 53.2° with the vertical. Calculate the distance of the centre of gravity from the left end.
Ans:
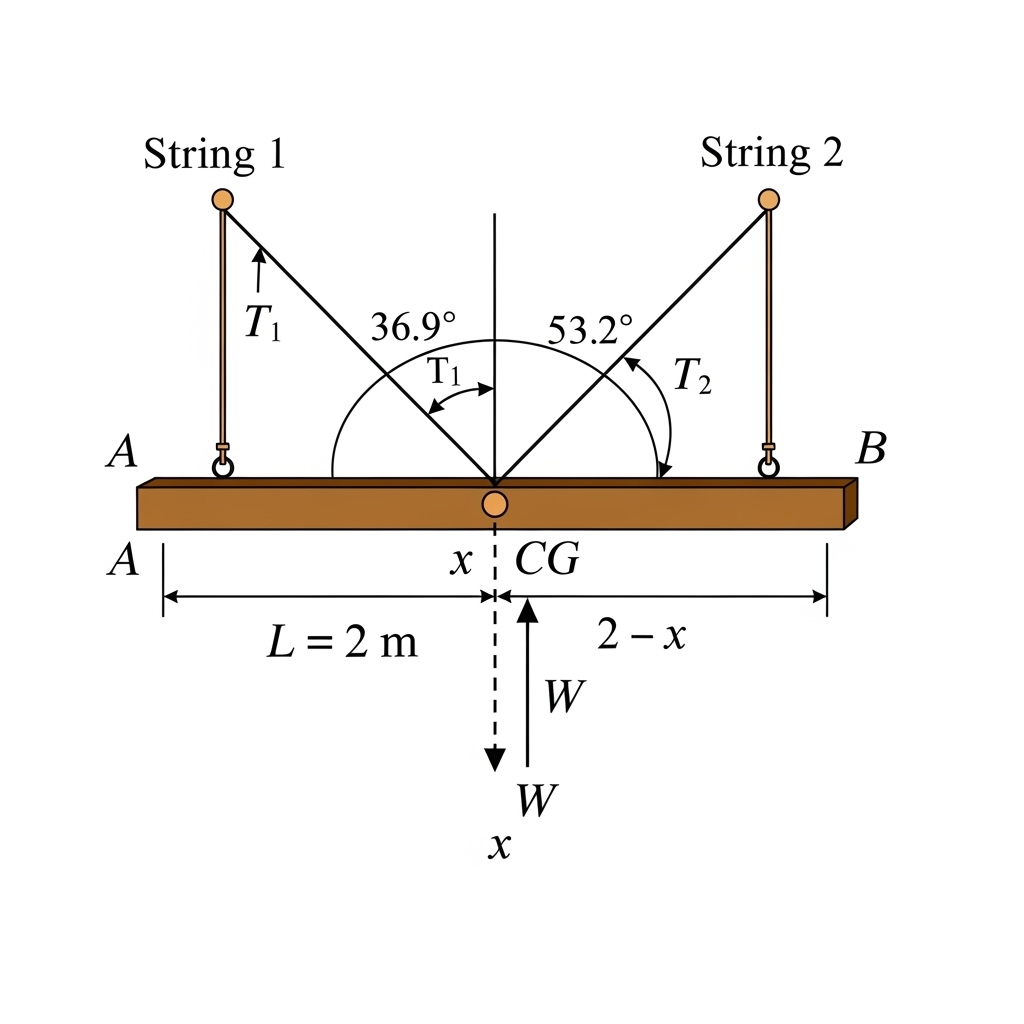
Let the tensions in the left and right strings be T1 and T2.
Horizontal equilibrium:
T1 sin 36.9° = T2 sin 53.2°
So, T1 / T2 = sin 53.2° / sin 36.9° = 0.8 / 0.6 = 4 / 3.
Hence, T1 = (4/3) T2.
Vertical equilibrium:
T1 cos 36.9° + T2 cos 53.2° = W.
Substitute values: cos 36.9° = 0.8, cos 53.2° = 0.6.
(4/3 T2)(0.8) + T2(0.6) = W.
1.0667 T2 + 0.6 T2 = W.
1.6667 T2 = W.
T2 = 0.6 W, and T1 = 0.8 W.
Taking moments about the left end:
Let the distance of the centre of gravity from the left end be x.
Moment of W = W × x.
Moment of T2 vertical component = (T2 cos 53.2°) × 2.
So, W × x = (0.6 W × 0.6) × 2 = 0.72 W.
Therefore, x = 0.72 m.
10. A car weighing 1800 kg has its centre of gravity 1.05 m behind the front axle, over a wheelbase of 1.8 m. Determine the force exerted by the ground on front and rear wheels.
Ans:
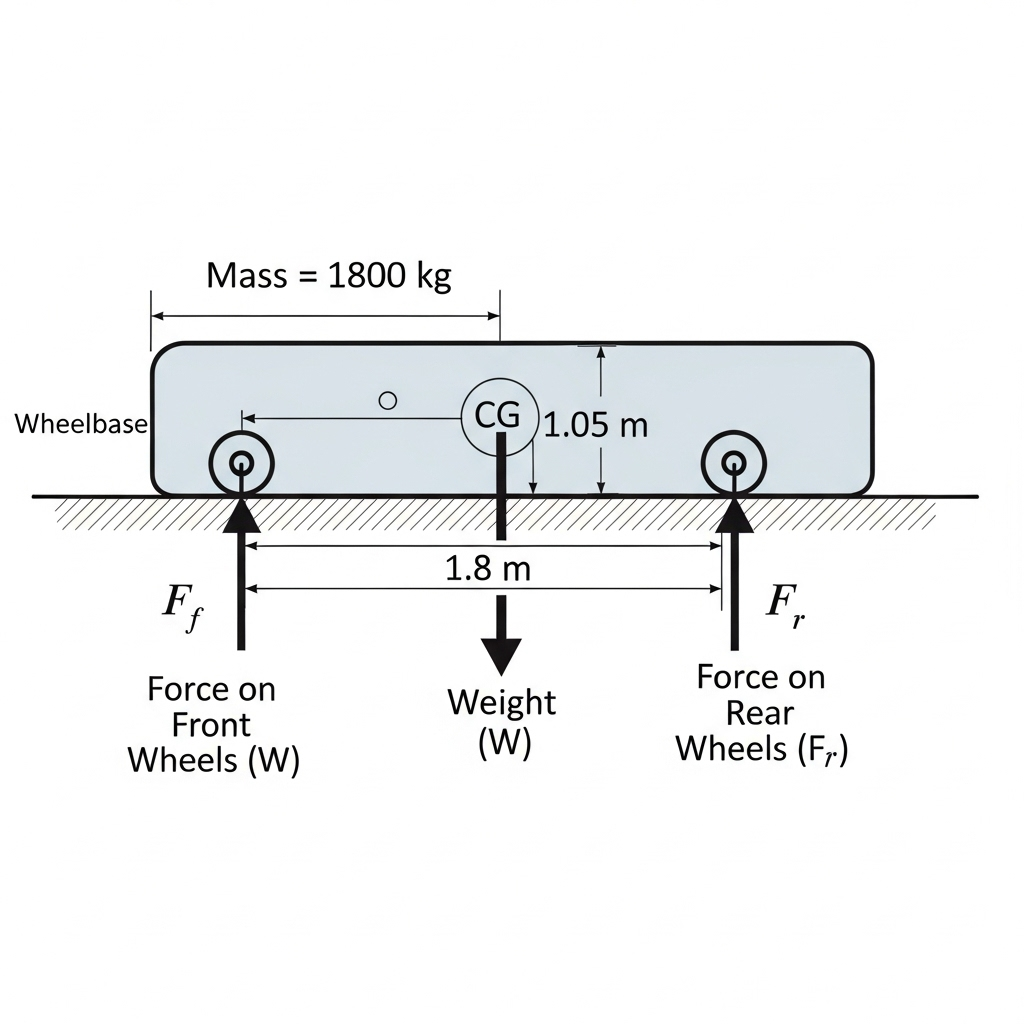
This is a problem of static equilibrium, where we can apply the principles of force and torque balance.
The forces acting on the car are its total weight acting downwards at the center of gravity, and the upward forces exerted by the ground on the front and rear wheels.
1. Calculate the Total Weight of the Car
First, we calculate the total weight of the car, which acts at its center of gravity. The formula for weight is: W=mg where m is the mass and g is the acceleration due to gravity (9.8m/s2).
- Mass (m) = 1800kg
- Acceleration due to gravity (g) = 9.8m/s2
W=1800kg×9.8m/s2=17640N
2. Determine the Force on the Rear Wheels
To find the force on the rear wheels (Fr), we can take the sum of the torques about the front axle and set it to zero, as the car is in equilibrium. Let’s consider the torques about the front axle:
- The torque due to the force on the front wheels is zero since it acts at the pivot point.
- The torque due to the car’s weight (W) acts clockwise.
- The torque due to the force on the rear wheels (Fr) acts counter-clockwise.
The equation for torque balance is:

3. Determine the Force on the Front Wheels
Now, we can find the force on the front wheels (Ff) by using the condition for force balance, where the sum of the upward forces equals the total downward force (the car’s weight).
11. Find the moment of inertia of given bodies using perpendicular and parallel axis theorems.
Ans:
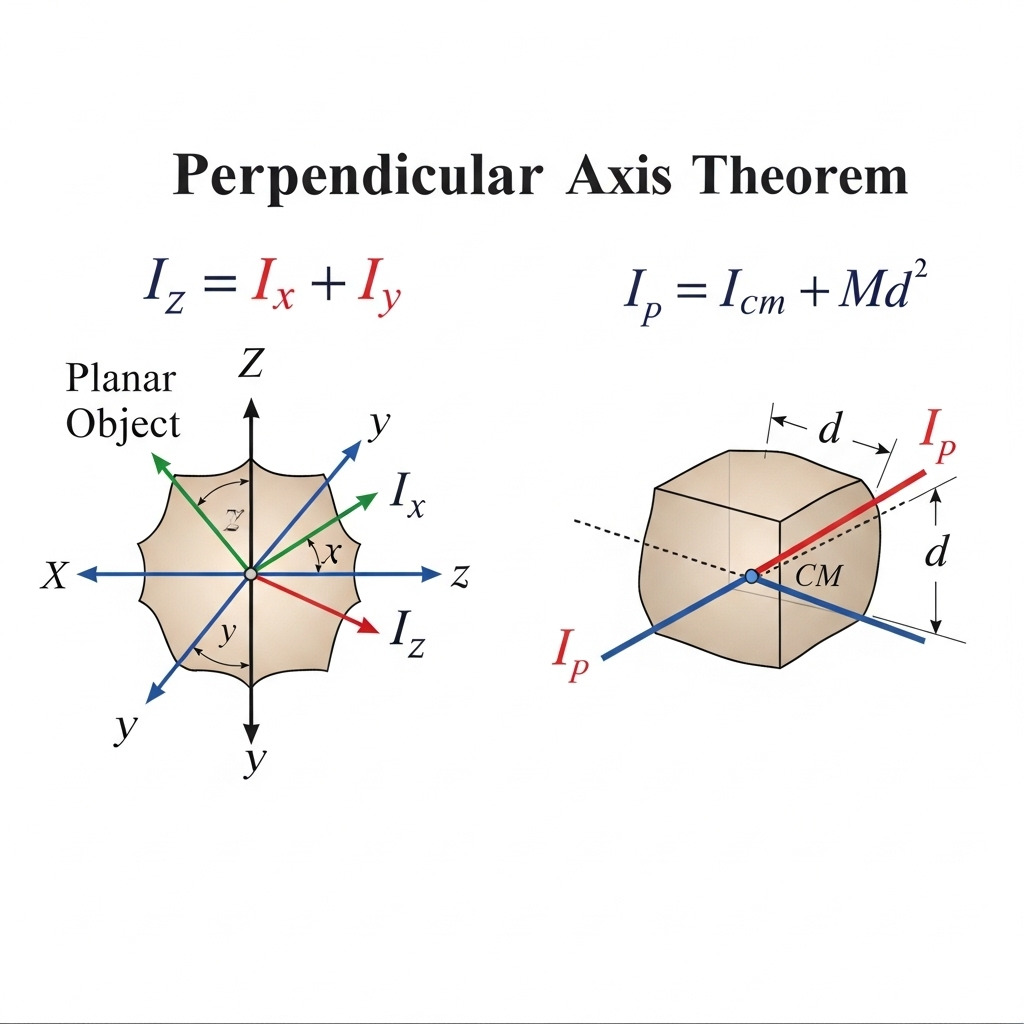
(A) Perpendicular Axis Theorem:
If a plane lamina lies in the XY–plane, then the moment of inertia about an axis perpendicular to the plane (Z–axis) is equal to the sum of the moments of inertia about two mutually perpendicular axes (X and Y) in the plane and intersecting at a point.
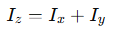
(B) Parallel Axis Theorem:
The moment of inertia of a body about any axis parallel to an axis through the centre of mass is given by
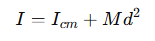



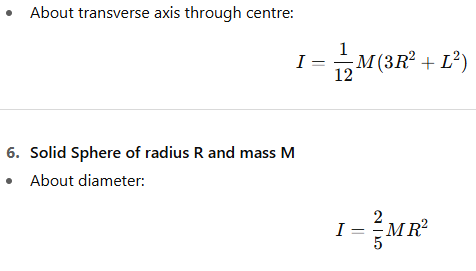
12. A uniform disc of radius R has a hole of radius R/2 cut out such that the center of the hole is at R/2 from the center of the disc. Locate the centre of gravity of the remaining body.
Ans:
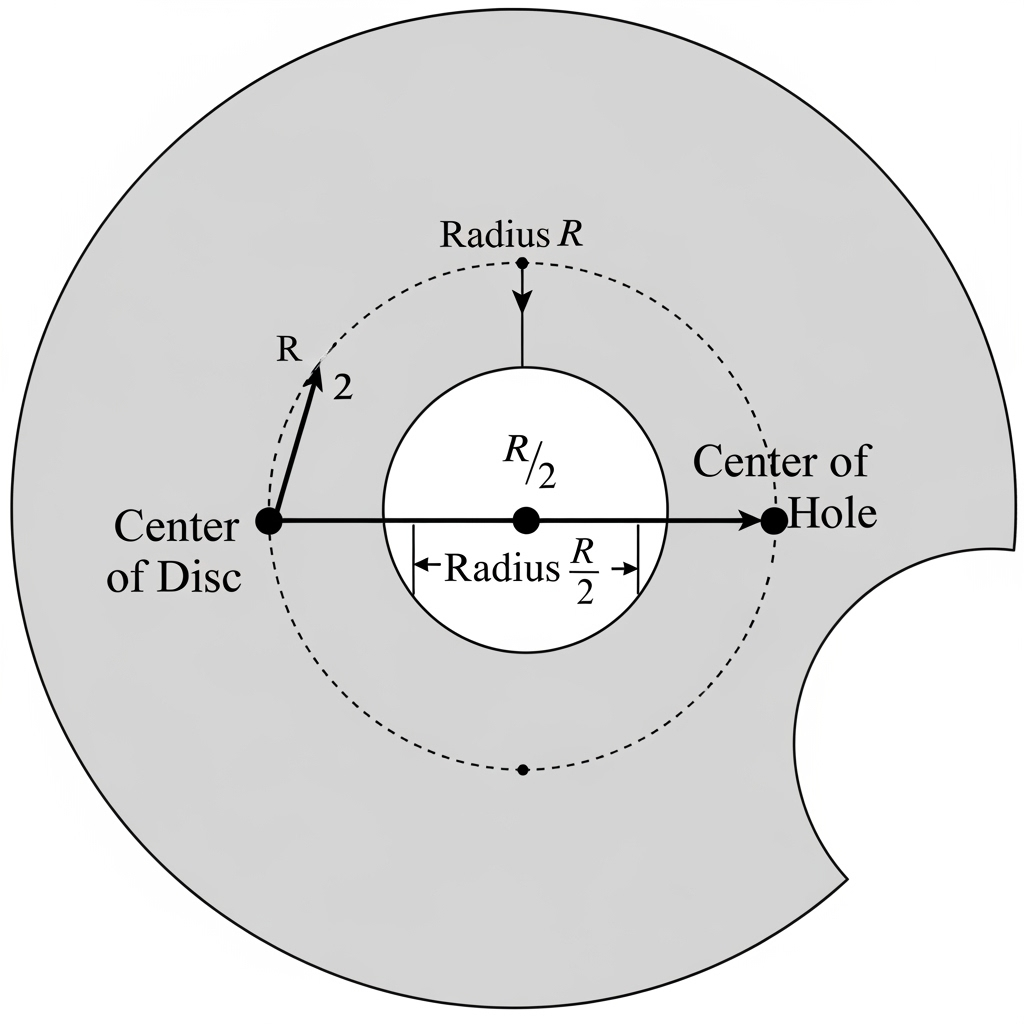
A uniform disc with a hole can be considered a composite body, and we can find its center of gravity (CG) using the principle of superposition. We can model the remaining body as a large complete disc with a positive mass, and a smaller disc (the hole) with a negative mass.
Let’s place the origin of our coordinate system at the center of the original, complete disc.
1. Define Mass and Center of Mass for Each Part
Since the disc is uniform, the mass is proportional to the area. Let σ be the surface mass density of the disc. The area

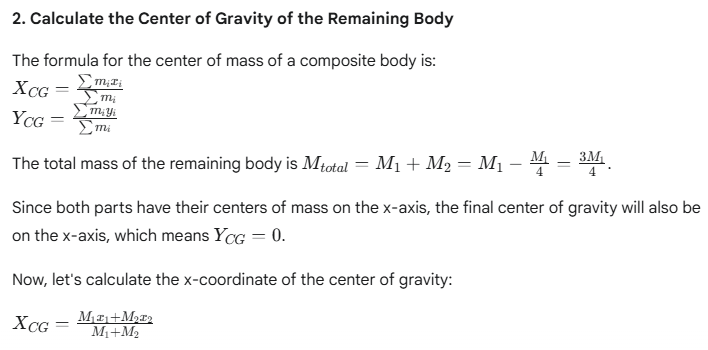
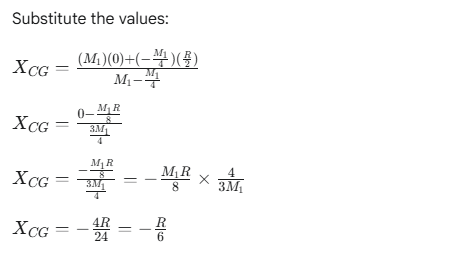
The negative sign indicates that the center of gravity has shifted from the origin in the opposite direction of the hole.
The center of gravity of the remaining body is at a distance of R/6 from the original center of the disc, on the side opposite to the hole.
13. A metre stick is balanced at its centre. When two coins of mass 5 g each are placed at the 12 cm mark, the knife edge shifts to balance at 45 cm. Find the mass of the metre stick.
Ans:
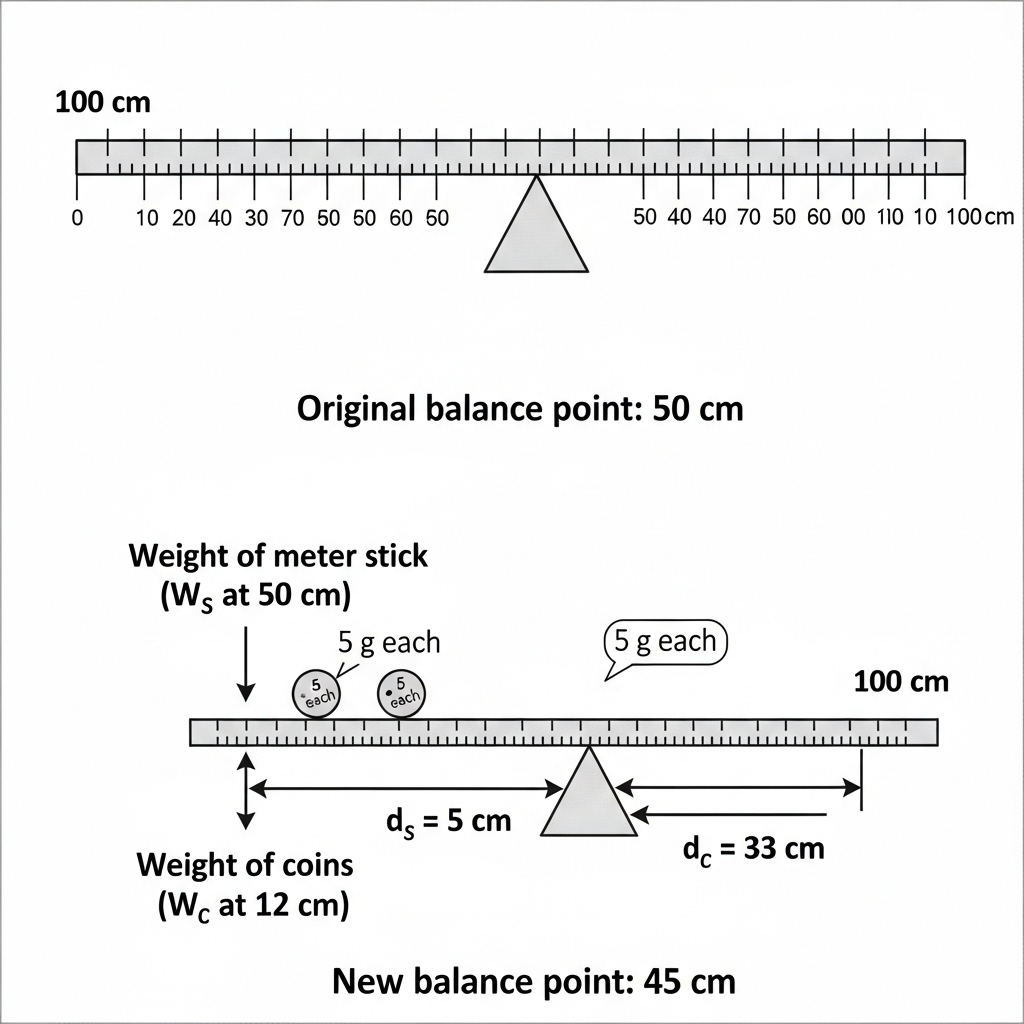
A metre stick is balanced at its centre. Mass of the stick = M grams.
Two coins of 5 g each are placed at the 12 cm mark. Total mass of coins = 10 g.
The balance point shifts to 45 cm.
Taking moments about 45 cm:
Moment due to stick = M × (50 – 45) = 5M
Moment due to coins = 10 × (45 – 12) = 10 × 33 = 330
For balance: 5M = 330
So, M = 330 ÷ 5 = 66 g
14. A solid sphere is released from rest at the top of two inclines of the same height but different angles.
(a) Does the sphere reach the bottom with the same speed?
(b) Does it take the same time? Explain.
Ans:
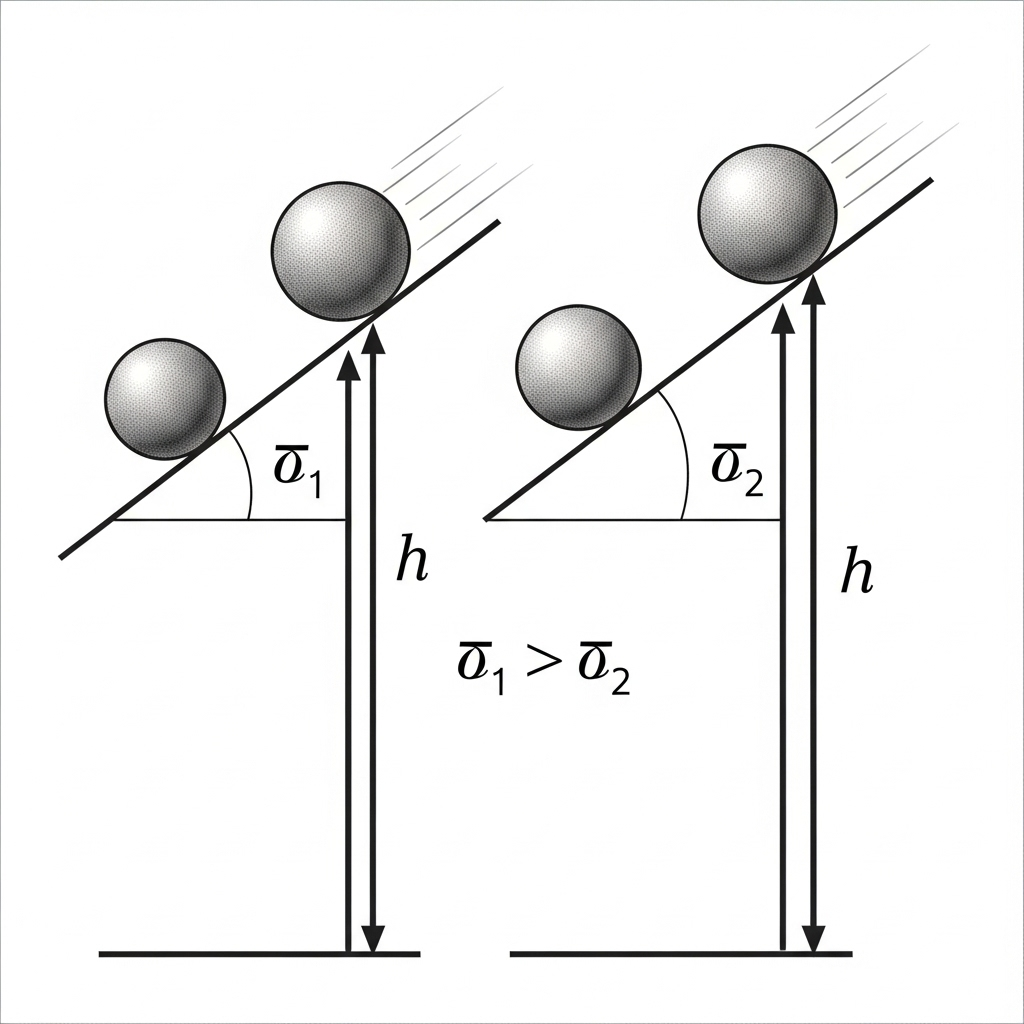
(a) Yes. If the solid sphere rolls without slipping and there is no energy loss, it reaches the bottom with the same speed for both inclines (because the final speed depends only on the drop in height, not the slope).
(b) No. The time is different — the steeper incline gives a larger acceleration, so the sphere reaches the bottom faster.
Now the explanation and derivation.
(a) Final speed — energy method
Assume pure rolling without slipping, no frictional energy loss. Initial potential energy mgh (height h) converts to translational plus rotational kinetic energy at bottom:

(b) Time to reach bottom — dynamics / kinematics
The acceleration of the rolling sphere down an incline of angle θ\thetaθ can be found from Newton’s laws + rolling constraint. For a rigid body with moment of inertia III,

15. A hoop (mass = 100 kg, radius = 2 m) rolls at 20 cm/s. How much work is needed to bring it to rest?
Ans:
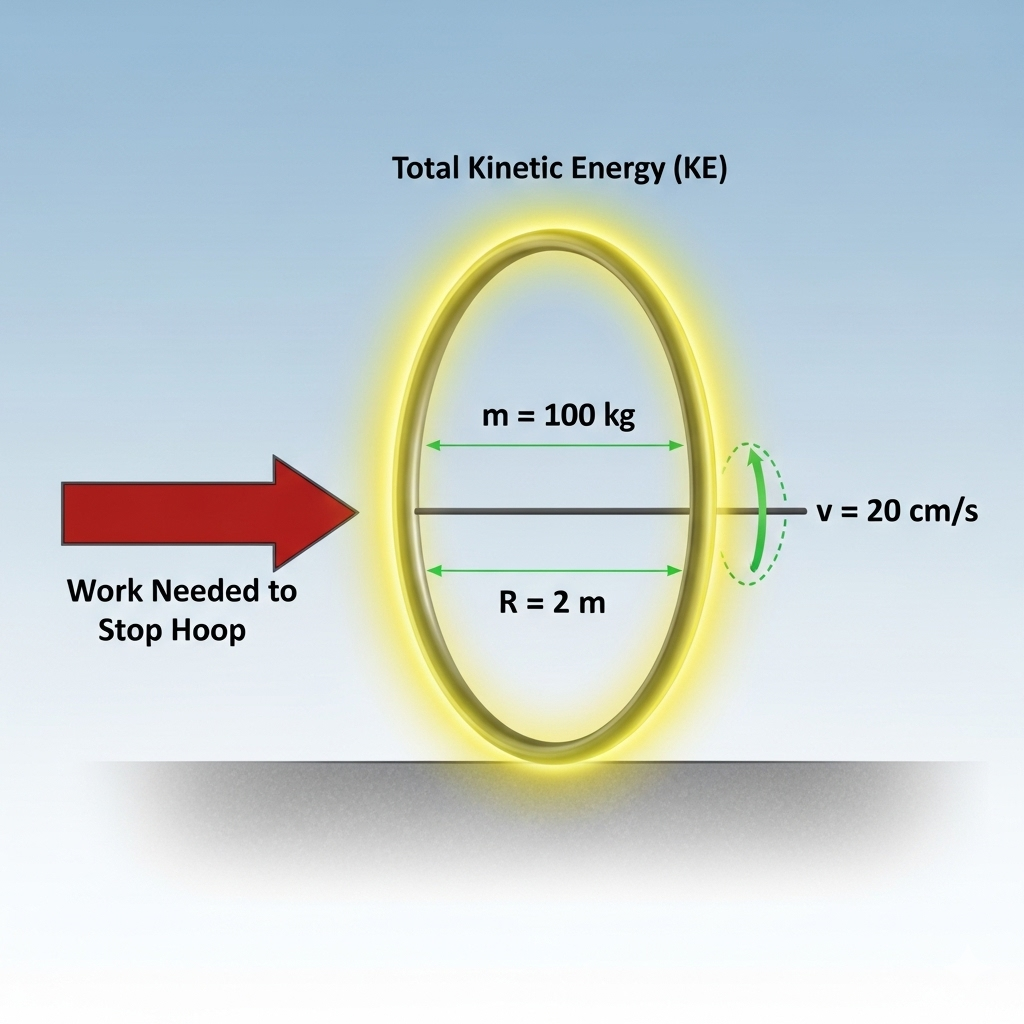
To bring the hoop to rest, the work done on it must be equal to its total initial kinetic energy. The total kinetic energy of a rolling object is the sum of its translational and rotational kinetic energy.
The work needed is 4 Joules.
1. Total Kinetic Energy

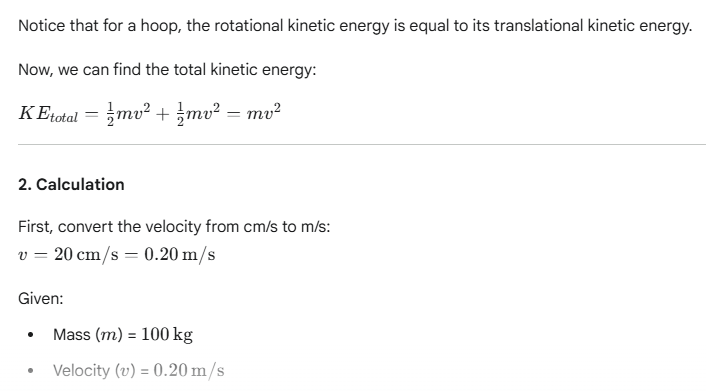

16. A solid cylinder with centre-of-mass speed 5 m/s is at the base of a plane inclined at 30°. Find:
(a) the height it reaches,
(b) the time taken to return to the bottom.
Ans:
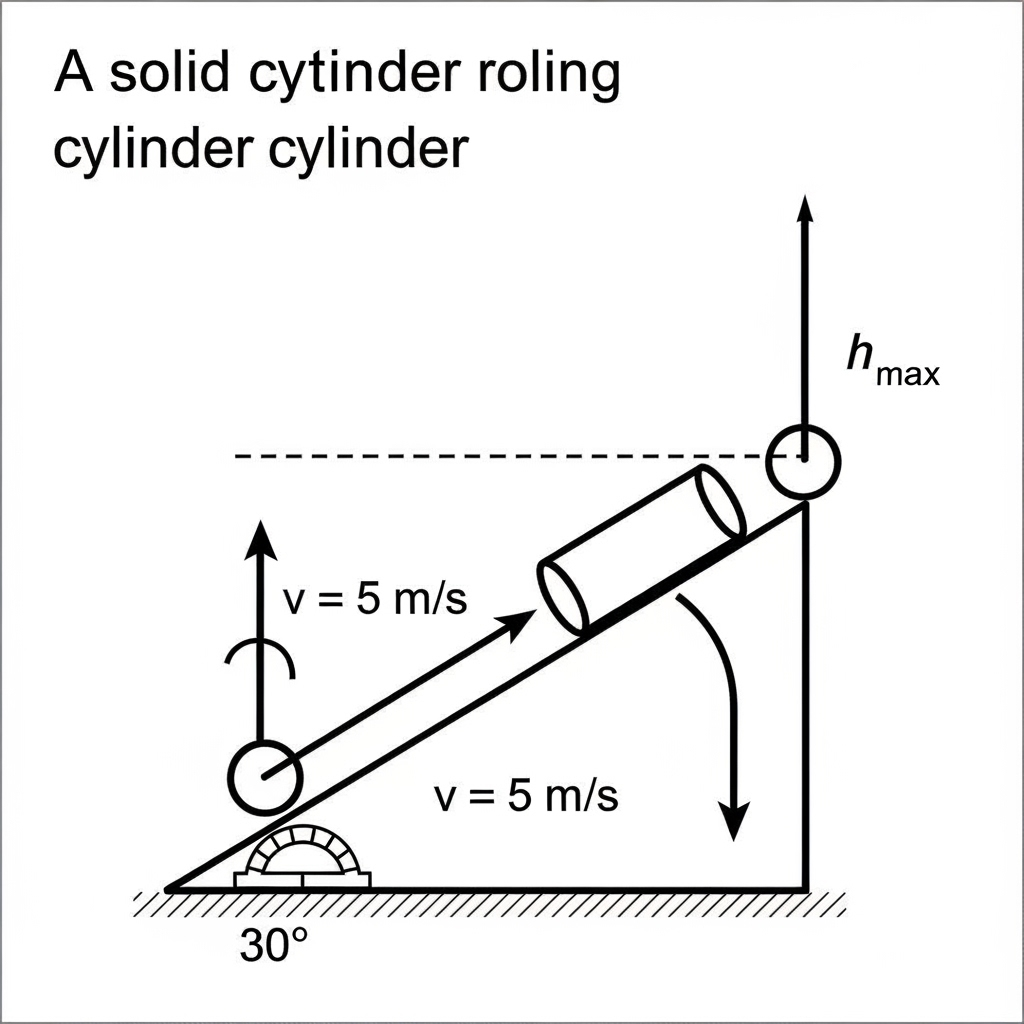
To solve this problem, we will use the principle of conservation of mechanical energy for the height calculation and kinematic equations with a force analysis for the time calculation. We assume the cylinder rolls without slipping.
(a) Height Reached by the Cylinder
The total initial energy of the cylinder at the base of the incline is purely kinetic, a combination of translational and rotational kinetic energy. At its maximum height, its energy is entirely potential. By the principle of conservation of energy, initial total kinetic energy equals final potential energy.

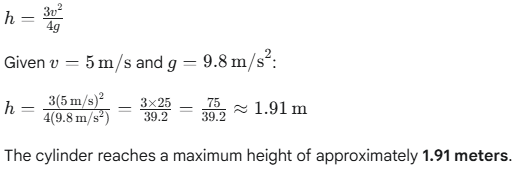
(b) Time Taken to Return to the Bottom
The motion is symmetrical; the time to roll up the incline is the same as the time to roll back down. Therefore, the total time is twice the time taken to reach the top. To find this time, we first need to determine the acceleration of the cylinder on the incline.
The acceleration of a solid cylinder rolling down an incline is given by:
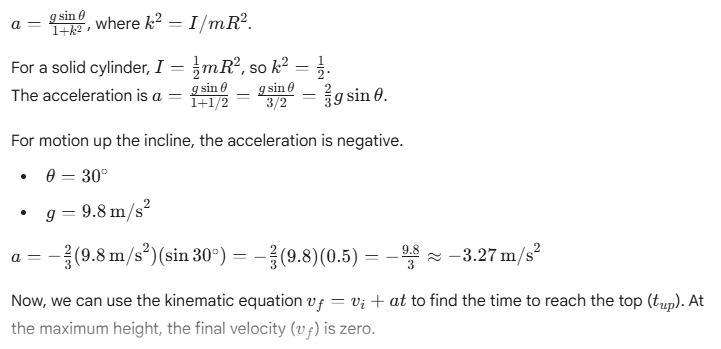

17. Prove that for a body with radius of gyration k and radius R rolling down an incline from rest,
v² = (2gh) / (1 + k²/R²).
Ans:
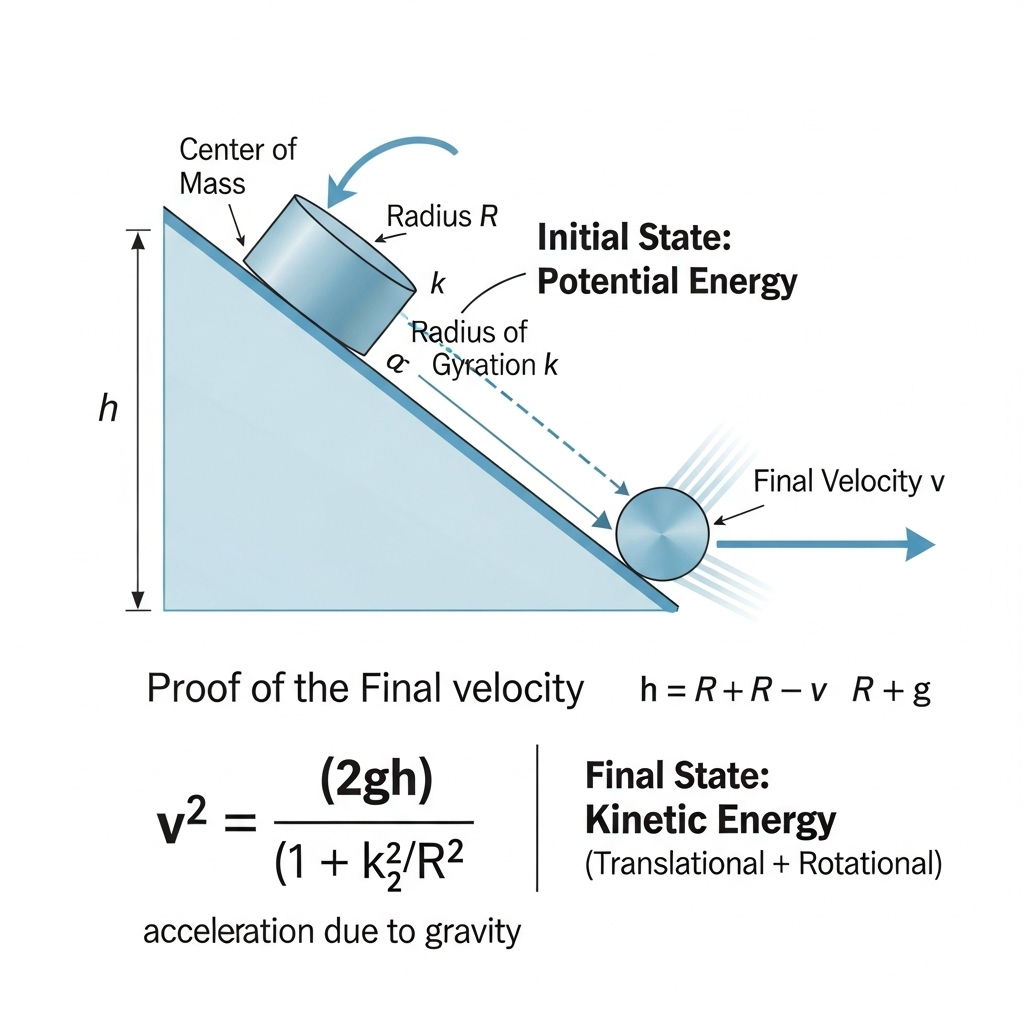
The statement can be proven by applying the principle of conservation of energy. For a body rolling down an incline from rest, the initial potential energy at the top is completely converted into translational and rotational kinetic energy at the bottom.
Proof
Let’s define the initial and final energy of the body:
Initial Energy (Einitial): At the top of the incline, the body starts from rest. Its initial kinetic energy is zero. All of its energy is potential energy (PE).



18. A disc spinning at angular velocity ω₀ is placed on a frictionless table. What are the linear velocities of points A, B, and C on the disc? Will the disc roll in a certain direction?
Ans:
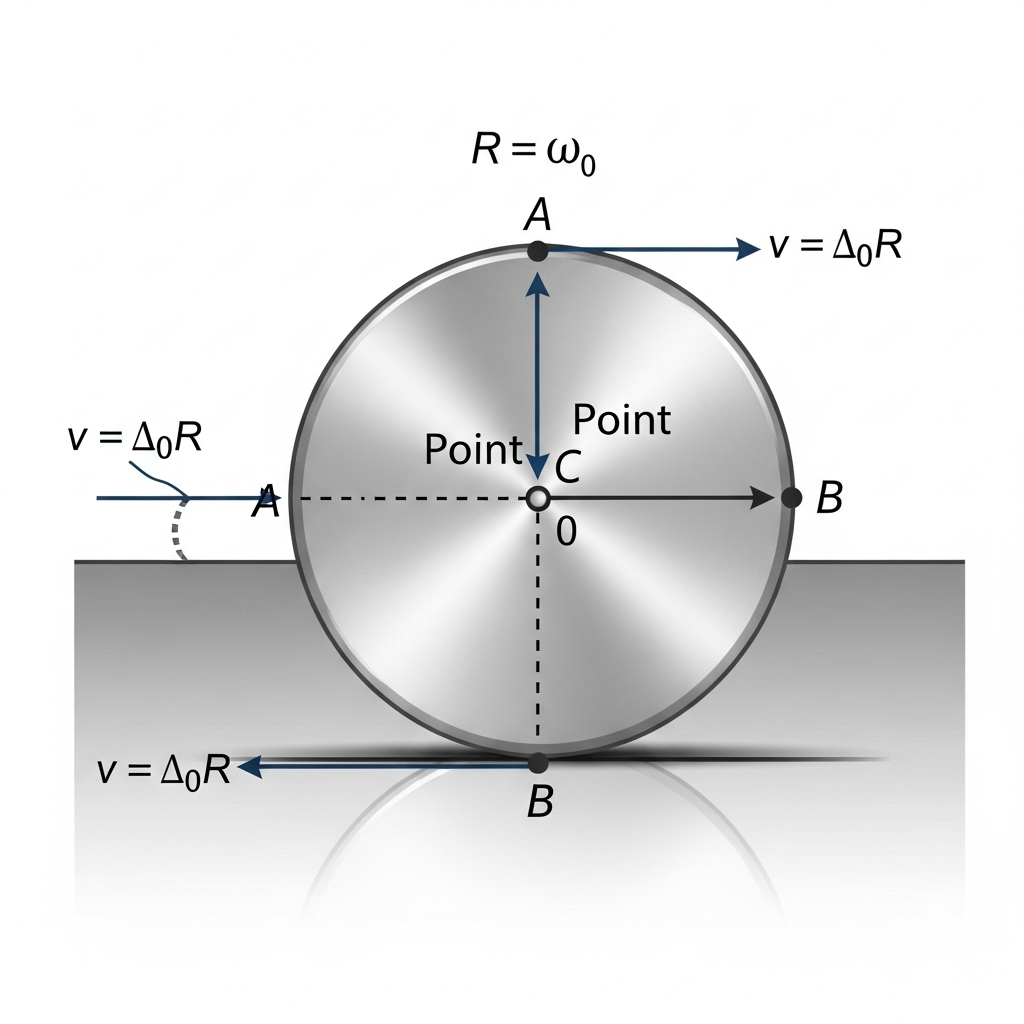


The problem states that the disc is on a frictionless table. A rolling object requires a force of static friction to create the torque that causes rotation and to provide the horizontal force that makes the center of mass move. In this case, with no friction, there is no net horizontal force to cause the center of mass to translate.
Therefore, the disc will only spin in place, and its center of mass will not move
19. (a) Why is friction necessary to start rolling?
(b) What is the direction of frictional force for a point B before rolling, and the torque sense?
(c) What is the force after perfect rolling starts?
Ans: (a) Why is friction necessary to start rolling?
Friction is necessary to start rolling because it provides the torque required for the body to rotate. Rolling motion is a combination of two types of motion:
- Translational motion: The center of mass of the body moves in a straight line.
- Rotational motion: The body spins about its center of mass.
An external force applied to the center of mass would only cause the body to slide or skid, as it provides no torque to initiate rotation. However, a force of static friction acting at the point of contact with the ground creates a torque about the center of mass. This torque causes the body to start spinning, linking the translational and rotational motions together to achieve rolling.
(b) Direction of Frictional Force and Torque
If a horizontal force is applied to the center of mass of a body at rest, the body will initially tend to skid forward. The force of static friction opposes this tendency to slip. Therefore:
- Direction of Frictional Force: The static frictional force acts forward, in the same direction as the intended motion of the body.
- Torque Sense: This forward-acting frictional force, applied at a distance from the center of mass, creates a torque that causes the body to rotate. The sense of this torque is such that it causes the body to spin in the direction of the rolling motion (e.g., a clockwise torque for a body rolling to the right).
(c) Force After Perfect Rolling Starts
After perfect rolling begins (i.e., without slipping), the force at the point of contact is the force of static friction. The magnitude of this force depends on the motion of the rolling body:
If the body is accelerating (either speeding up or slowing down), a non-zero static frictional force is required to produce the necessary torque for the change in angular velocity. The magnitude of this force is just enough to prevent slipping.
If the body is rolling at a constant velocity on a horizontal surface, the net force and net torque are both zero. In this ideal case, the static frictional force required to maintain the rolling condition is also zero.
20. A solid disc and a ring are set into rotation with the same angular speed on a rough surface. Which one will start rolling first if μₖ = 0.2?
Ans:
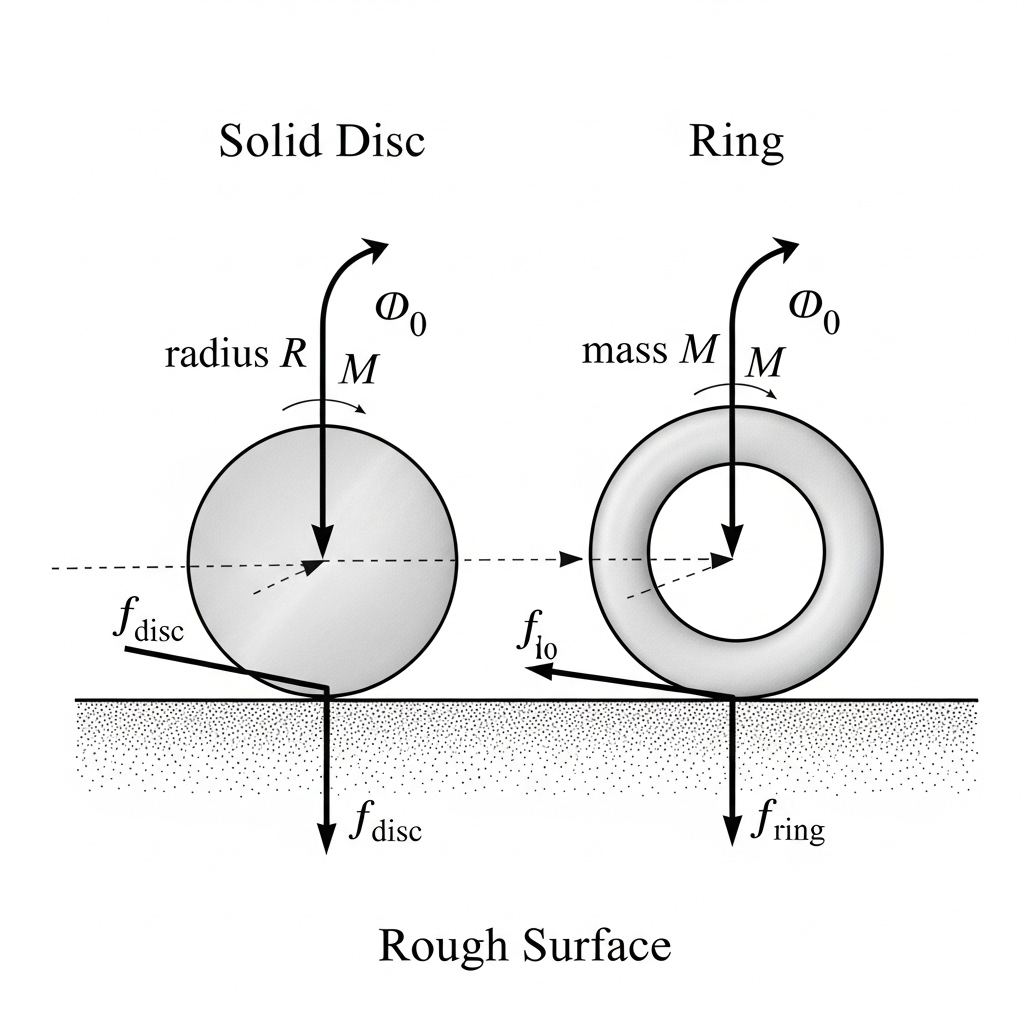




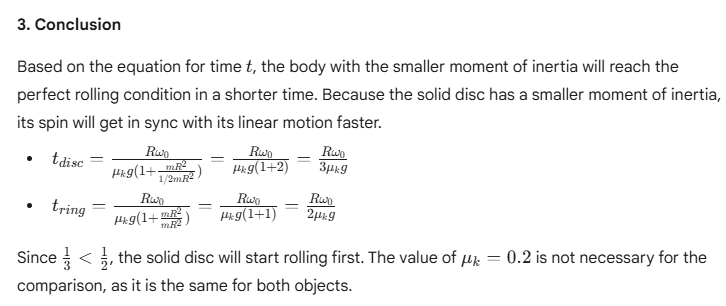
21. A 10 kg cylinder (radius 15 cm) rolls without slipping on a 30° incline. Coefficient of static friction μₛ = 0.25.
(a) Find the frictional force.
(b) Find the work done against friction during rolling.
(c) At what incline angle does it begin to skid?
Ans:
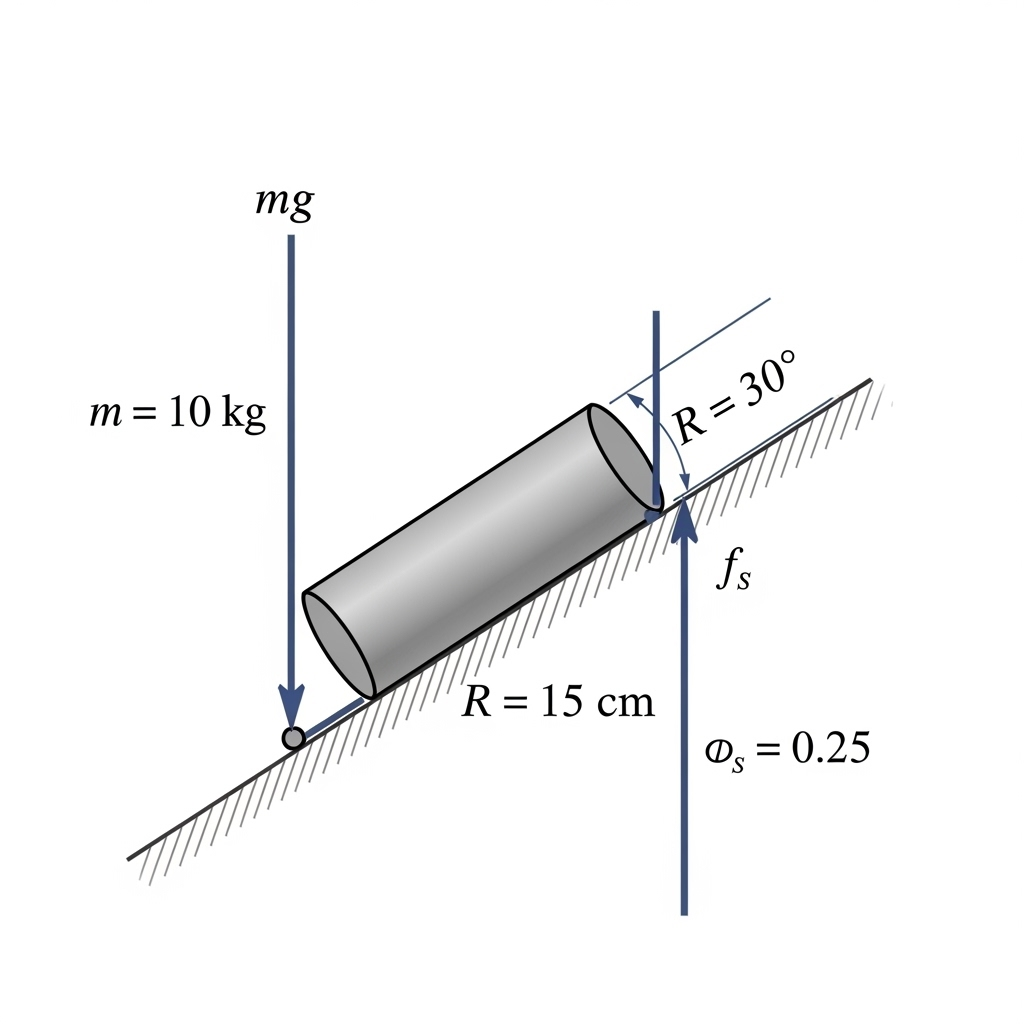
(a) Frictional Force
The frictional force is the static friction that prevents the cylinder from slipping. We can find its value by applying Newton’s second law for both translational and rotational motion.


(b) Work Done Against Friction
The work done by a force is given by W=F⋅d
. For an object rolling without slipping, the point of contact where the static frictional force acts is instantaneously at rest relative to the ground. Since the point of application of the frictional force has zero displacement, the work done by the force of static friction is zero.
Therefore, the work done against friction during rolling is zero.

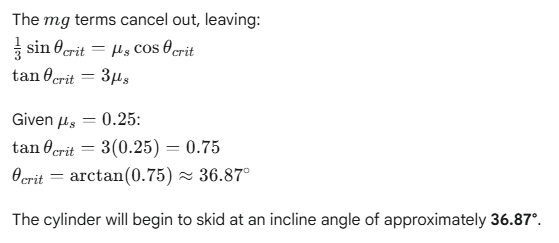
Practice for JEE/NEET
- Assertion-Reason questions on torque and COM
- Conceptual MCQs on angular momentum
- Numerical questions on moment of inertia
Conclusion
The chapter System of Particles and Rotational Motion links linear and rotational motion. By understanding torque, angular momentum, equilibrium, and MI, students can solve problems related to rigid bodies and prepare strongly for board exams and competitive exams.
Class 11 Physics NCERT Solutions-All Chapters-OLD SYLLABUS
Chapter-wise Links:
- Chapter 1: Physical World
- Chapter 2: Units and Measurements
- Chapter 3: Motion in a Straight Line
- Chapter 4: Motion in a Plane
- Chapter 5: Laws of Motion
- Chapter 6: Work, Energy and Power
- Chapter 7: System of Particles and Rotational Motion
- Chapter 8: Gravitation
- Chapter 9: Mechanical Properties of Solids
- Chapter 10: Mechanical Properties of Fluids
- Chapter 11: Thermal Properties of Matter
- Chapter 12: Thermodynamics
- Chapter 13: Kinetic Theory
- Chapter 14: Oscillations
- Chapter 15: Waves
For the official Class 11 Physics Solutions, you can visit:
- NCERT Textbooks
Class-wise Solutions
Class 12:
Class 12 Physics – NCERT Solutions
Class 12 Chemistry – NCERT Solutions
Class 11:
- Class 11 Physics – NCERT Solutions
- Class 11 Chemistry – NCERT Solutions
- Class 11 Biology – NCERT Solutions
- Class 11 Math – NCERT Solutions
Class 10:
Class 9:
Class 8:
Class 7:
Class 6:
Subject-wise Solutions
Physics:
Chemistry:
Biology:
Math:
- Class 11 Math – NCERT Solutions
- Class 10 Math – NCERT Solutions
- Class 9 Math – NCERT Solutions
- Class 8 Math – NCERT Solutions
Science:
- Class 10 Science – NCERT Solutions
- Class 9 Science – NCERT Solutions
- Class 8 Science – Oxford Solutions
- Class 7 Science – Oxford Solutions
- Class 6 Science – Oxford Solutions
