Class 8 Math Ch 6 Squares and Square Roots Ex 6.2 focuses on methods to find the square roots of numbers, especially through prime factorisation and estimation techniques. This exercise helps students understand how to break down a number into its prime factors and use them to find the square root easily. It also introduces the process of estimating square roots for non-perfect squares, improving number sense and calculation accuracy. Class 8 Math Ch 6 Squares and Square Roots Ex 6.2 builds critical problem-solving skills that are useful in algebra, geometry, and real-life applications involving measurements and areas.

Class 8 Math Ch 6 Squares and Square Roots Ex 6.2 – Textbook Answers

  1. Question 1.
    Find the square of the following numbers.
    (i) 32
    (ii) 35
    (iii) 86
    (iv) 93
    (v) 71
    (vi) 46
    Solution:
    (i) 32 = 30 + 2
    (32)2 = (30 + 2)2
    = 30(30 + 2) + 2(30 + 2)
    = 302 + 30 × 2 + 2 × 30 + 22
    = 900 + 60 + 60 + 4
    = 1024
    Thus (32)2 = 1024

(ii) 35 = (30 + 5)
(35)2 = (30 + 5)2
= 30(30 + 5) + 5(30 + 5)
= (30)2 + 30 × 5 + 5 × 30 + (5)2
= 900 + 150 + 150 + 25
= 1225
Thus (35)2 = 1225

(iii) 86 = (80 + 6)
862 = (80 + 6)2
= 80(80 + 6) + 6(80 + 6)
= (80)2 + 80 × 6 + 6 × 80 + (6)2
= 6400 + 480 + 480 + 36
= 7396
Thus (86)2 = 7396

(iv) 93 = (90+ 3)
932 = (90 + 3)2
= 90 (90 + 3) + 3(90 + 3)
= (90)2 + 90 × 3 + 3 × 90 + (3)2
= 8100 + 270 + 270 + 9
= 8649
Thus (93)2 = 8649

(v) 71 = (70 + 1)
712 = (70 + 1)2
= 70 (70 + 1) + 1(70 + 1)
= (70)2 + 70 × 1 + 1 × 70 + (1)2
= 4900 + 70 + 70 + 1
= 5041
Thus (71)2 = 5041

(vi) 46 = (40+ 6)
462 = (40 + 6)2
= 40 (40 + 6) + 6(40 + 6)
= (40)2 + 40 × 6 + 6 × 40 + (6)2
= 1600 + 240 + 240 + 36
= 2116
Thus (46)2 = 2116

Ex 6.2 Class 8 Maths Question 2.
Write a Pythagorean triplet whose one member is
(i) 6
(ii) 14
(iii) 16
(iv) 18
Solution:
(i) Let m2 – 1 = 6
[Triplets are in the form 2m, m2 – 1, m2 + 1]
m2 = 6 + 1 = 7
So, the value of m will not be an integer.
Now, let us try for m2 + 1 = 6
⇒ m2 = 6 – 1 = 5
Also, the value of m will not be an integer.
Now we let 2m = 6 ⇒ m = 3 which is an integer.
Other members are:
m2 – 1 = 32 – 1 = 8 and m2 + 1 = 32 + 1 = 10
Hence, the required triplets are 6, 8 and 10

(ii) Let m2 – 1 = 14 ⇒ m2 = 1 + 14 = 15
The value of m will not be an integer.
Now take 2m = 14 ⇒ m = 7 which is an integer.
The member of triplets are 2m = 2 × 7 = 14
m2 – 1 = (7)2 – 1 = 49 – 1 = 48
and m2 + 1 = (7)2 + 1 = 49 + 1 = 50
i.e., (14, 48, 50)

(iii) Let 2m = 16 m = 8
The required triplets are 2m = 2 × 8 = 16
m2 – 1 = (8)2 – 1 = 64 – 1 = 63
m2 + 1 = (8)2 + 1 = 64 + 1 = 65
i.e., (16, 63, 65)

(iv) Let 2m = 18 ⇒ m = 9
Required triplets are:
2m = 2 × 9 = 18
m2 – 1 = (9)2 – 1 = 81 – 1 = 80
and m2 + 1 = (9)2 + 1 = 81 + 1 = 82
i.e., (18, 80, 82)

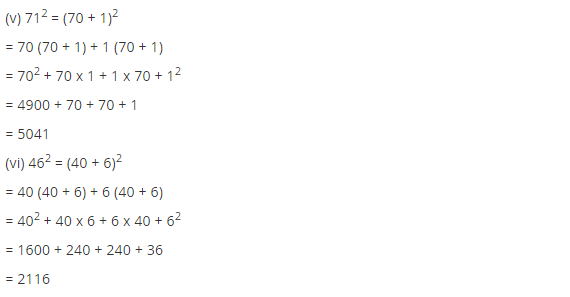
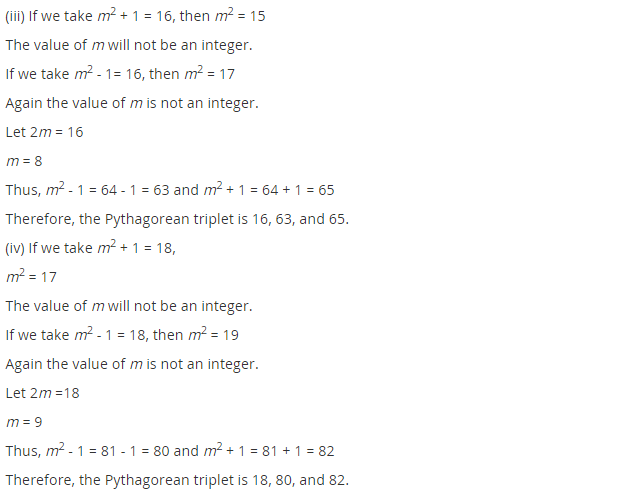
Class 8 Math Ch 6 Squares and Square Roots Ex 6.2
Class 8 Math Ch 6 Squares and Square Roots Ex 6.2
NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2 Q2
Class 8 Math Ch 6 Squares and Square Roots Ex 6.2
CLASS 8 MATH EX 6.3

📘 Math & Science Solutions by Class

🔹 Class 10

🔹 Class 9

🔹 Class 8

🔹 Class 7

🔹 Class 6

🔹 Class 12

🔹 Class 11

For the official Class 8 Mathematics Solutions, you can visit:

  1. NCERT Textbooks (for Class 8):
NCERT TEXTBOOK