Class 8 Math Ch 7 Cubes and Cube Roots Ex 7.1 introduces students to the concept of cube numbers and how to find the cube of a given number. This exercise helps build a strong foundation in number operations by exploring patterns in cubes and identifying perfect cube numbers. Through simple problems, students learn to recognize the structure of cube numbers and understand their mathematical significance. Practicing Class 8 Math Ch 7 Cubes and Cube Roots Ex 7.1 improves logical thinking and prepares students for advanced topics like cube roots and algebraic identities.
Class 8 Math Ch 7 Cubes and Cube Roots Ex 7.1 Textbook Answers
Ex 7.1 Class 8 Maths Question 1.
Which of the following numbers are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
Solution:
(i) Prime factorisation of 216 is:
216 = 2 × 2 × 2 × 3 × 3 × 3
In the above factorisation, 2 and 3 have formed a group of three.
Thus, 216 is a perfect cube.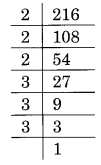
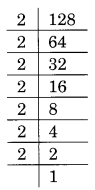
(ii) Prime factorisation of 128 is:
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Here, 2 is left without making a group of three.
Thus 128 is not a perfect cube.
(iii) Prime factorisation of 1000, is:
1000 = 2 × 2 × 2 × 5 × 5 × 5
Here, no number is left for making a group of three.
Thus, 1000 is a perfect cube.

(iv) Prime factorisation of 100, is:
100 = 2 × 2 × 5 × 5
Here 2 and 5 have not formed a group of three.
Thus, 100 is not a perfect cube.

(v) Prime factorisation of 46656 is:
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Here 2 and 3 have formed the groups of three.
Thus, 46656 is a perfect cube.

Ex 7.1 Class 8 Maths Question 2.
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
Solution:
(i) Prime factorisation of 243, is:
243 = 3 × 3 × 3 × 3 × 3 = 33 × 3 × 3
Here, number 3 is required to make 3 × 3 a group of three, i.e., 3 × 3 × 3
Thus, the required smallest number to be multiplied is 3.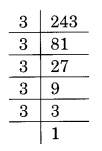
(ii) Prime factorisation of 256, is:
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 23 × 23 × 2 × 2
Here, a number 2 is needed to make 2 × 2 a group of three, i.e., 2 × 2 × 2
Thus, the required smallest number to be multiplied is 2.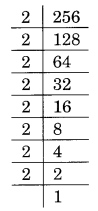
(iii) Prime factorisation of 72, is:
72 = 2 × 2 × 2 × 3 × 3 = 23 × 3 × 3
Here, a number 3 is required to make 3 × 3 a group of three, i.e. 3 × 3 × 3
Thus, the required smallest number to be multiplied is 3.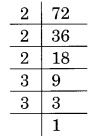
(iv) Prime factorisation of 675, is:
675 = 3 × 3 × 3 × 5 × 5 = 33 × 5 × 5
Here, a number 5 is required to make 5 × 5 a group of three to make it a perfect cube, i.e. 5 × 5 × 5
Thus, the required smallest number is 5.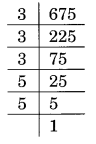
(v) Prime factorisation of 100, is:
100 = 2 × 2 × 5 × 5
Here, number 2 and 5 are needed to multiplied 2 × 2 × 5 × 5 to make it a perfect cube, i.e., 2 × 2 × 2 × 5 × 5 × 5
Thus, the required smallest number to be multiplied is 2 × 5 = 10.
Ex 7.1 Class 8 Maths Question 3.
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 92
(v) 704
Solution:
(i) Prime factorisation of 81, is:
81 = 3 × 3 × 3 × 3 = 33 × 3
Here, a number 3 is the number by which 81 is divided to make it a perfect cube,
i.e., 81 ÷ 3 = 27 which is a perfect cube.
Thus, the required smallest number to be divided is 3.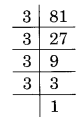
(ii) Prime factorisation of 128, is:
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 23 × 23 × 2
Here, a number 2 is the smallest number by which 128 is divided to make it a perfect cube,
i.e., 128 ÷ 2 = 64 which is a perfect cube.
Thus, 2 is the required smallest number.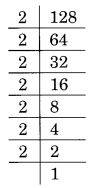
(iii) Prime factorisation of 135 is:
135 = 3 × 3 × 3 × 5 = 33 × 5
Here, 5 is the smallest number by which 135 is divided to make a perfect cube,
i.e., 135 ÷ 5 = 27 which is a perfect cube.
Thus, 5 is the required smallest number.
(iv) Prime factorisation of 192 is:
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 23 × 23 × 3
Here, 3 is the smallest number by which 192 is divided to make it a perfect cube,
i.e., 192 ÷ 3 = 64 which is a perfect cube.
Thus, 3 is the required smallest number.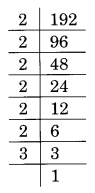
(v) Prime factorisation of 704 is:
704 = 2 × 2 × 2 × 2 × 2 × 2 × 11 = 23 × 23 × 11
Here, 11 is the smallest number by which 704 is divided to make it a perfect cube,
i.e., 704 ÷ 11 = 64 which is a perfect cube.
Thus, 11 is the required smallest number.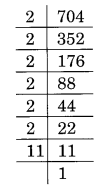
Ex 7.1 Class 8 Maths Question 4.
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will be needed to form a cube?
Solution:
The sides of the cuboid are given as 5 cm, 2 cm and 5 cm.
Volume of the cuboid = 5 cm × 2 cm × 5 cm = 50 cm3
For the prime factorisation of 50, we have
50 = 2 × 5 × 5
To make it a perfect cube, we must have
2 × 2 × 2 × 5 × 5 × 5
= 20 × (2 × 5 × 5)
= 20 × volume of the given cuboid
Thus, the required number of cuboids = 20.
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 8 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 8):
