Exercise 14.1 of Chapter 14 – Factorisation introduces the basic methods of factorising algebraic expressions. In this exercise, students learn how to take out common factors and simplify expressions step by step. It builds the foundation for solving more complex algebraic problems.
Class 8 Maths Chapter14 Factorisation Ex14.1-NCERT Textbook
Ex 14.1 Class 8 Maths Question 1.
Find the common factors of the given terms.
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14pq, 28p2q2
(iv) 2x, 3x2, 4
(v) 6abc, 24ab2, 12a2b
(vi) 16x3, -4x2, 32x
(vii) 10pq, 20qr, 30rp
(viii) 3x2y3, 10x3y2, 6x2y2z
Solution:
(i) 12x, 36
(2 × 2 × 3 × x) and (2 × 2 × 3 × 3)
Common factors are 2 × 2 × 3 = 12
Hence, the common factor = 12
(ii) 2y, 22xy
= (2 × y) and (2 × 11 × x × y)
Common factors are 2 × y = 2y
Hence, the common factor = 2y
(iii) 14pq, 28p2q2
= (2 × 7 × p × q) and (2 × 2 × 7 × p × p × q × q)
Common factors are 2 × 7 × p × q = 14pq
Hence, the common factor = 14pq
(iv) 2x, 3x2, 4
= (2 × x), (3 × x × x) and (2 × 2)
Common factor is 1
Hence, the common factor = 1 [∵ 1 is a factor of every number]
(v) 6abc, 24ab2, 12a2b
= (2 × 3 × a × b × c), (2 × 2 × 2 × 3 × a × b × b) and (2 × 2 × 3 × a × a × b)
Common factors are 2 × 3 × a × b = 6ab
Hence, the common factor = 6ab
(vi) 16x3, -4x2, 32x
= (2 × 2 × 2 × 2 × x × x × x), -(2 × 2 × x × x), (2 × 2 × 2 × 2 × 2 × x)
Common factors are 2 × 2 × x = 4x
Hence, the common factor = 4x
(vii) 10pq, 20qr, 30rp
= (2 × 5 × p × q), (2 × 2 × 5 × q × r), (2 × 3 × 5 × r × p)
Common factors are 2 × 5 = 10
Hence, the common factor = 10
(viii) 3x2y2, 10x3y2, 6x2y2z
= (3 × x × x × y × y), (2 × 5 × x × x × x × y × y), (2 × 3 × x × x × y × y × z)
Common factors are x × x × y × y = x2y2
Hence, the common factor = x2y2.
Ex 14.1 Class 8 Maths Question 2.
Factorise the following expressions.
(i) 7x – 42
(ii) 6p – 12q
(iii) 7a2 + 14a
(iv) -16z + 20z3
(v) 20l2m + 30alm
(vi) 5x2y – 15xy2
(vii) 10a2 – 15b2 + 20c2
(viii) -4a2 + 4ab – 4ca
(ix) x2yz + xy2z + xyz2
(x) ax2y + bxy2 + cxyz
Solution:
(i) 7x – 42 = 7(x – 6)
(ii) 6p – 12q = 6(p – 2q)
(iii) 7a2 + 14a = 7a(a + 2)
(iv) -16z + 20z3 = 4z(-4 + 5z2)
(v) 20l2m + 30alm = 10lm(2l + 3a)
(vi) 5x2y – 15xy2 = 5xy(x – 3y)
(vii) 10a2 – 15b2 + 20c2 = 5(2a2 – 3b2 + 4c2)
(viii) -4a2 + 4ab – 4ca = 4a(-a + b – c)
(ix) x2yz + xy2z + xyz2 = xyz(x + y + z)
(x) ax2y + bxy2 + cxyz = xy(ax + by + cz)
Ex 14.1 Class 8 Maths Question 3.
Factorise:
(i) x2 + xy + 8x + 8y
(ii) 15xy – 6x + 5y – 2
(iii) ax + bx – ay – by
(iv) 15pq + 15 + 9q + 25p
(v) z – 7 + 7xy – xyz
Solution:
(i) x2 + xy + 8x + 8y
Grouping the terms, we have
x2 + xy + 8x + 8y
= x(x + y) + 8(x + y)
= (x + y)(x + 8)
Hence, the required factors = (x + y)(x + 8)
(ii) 15xy – 6x + 5y – 2
Grouping the terms, we have
(15xy – 6x) + (5y – 2)
= 3x(5y – 2) + (5y – 2)
= (5y – 2)(3x + 1)
(iii) ax + bx – ay – by
Grouping the terms, we have
= (ax – ay) + (bx – by)
= a(x – y) + b(x – y)
= (x – y)(a + b)
Hence, the required factors = (x – y)(a + b)
(iv) 15pq + 15 + 9q + 25p
Grouping the terms, we have
= (15pq + 25p) + (9q + 15)
= 5p(3q + 5) + 3(3q + 5)
= (3q + 5) (5p + 3)
Hence, the required factors = (3q + 5) (5p + 3)
(v) z – 7 + 7xy – xyz
Grouping the terms, we have
= (-xyz + 7xy) + (z – 7)
= -xy(z – 7) + 1 (z – 7)
= (-xy + 1) (z – 1)
Hence the required factor = -(1 – xy) (z – 7)


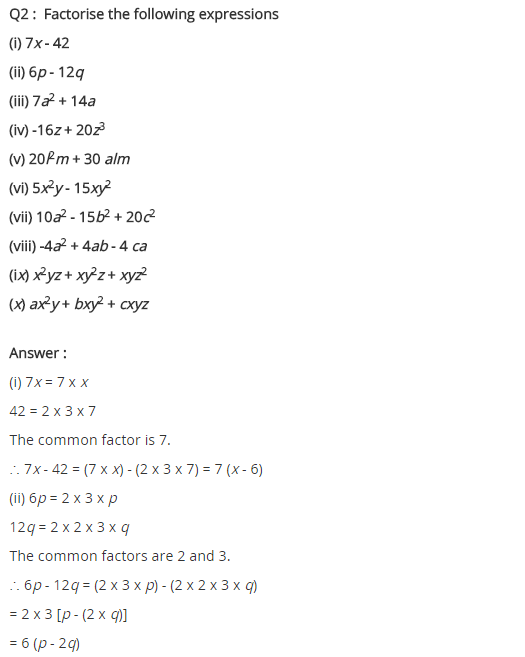



📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
