Class 8 Maths Exercise 2.6 Easy Solutions NCERT delves into solving more advanced linear equations involving fractions and decimal terms. This exercise is aimed at helping students improve their skills in handling equations with multiple steps. The solutions provided are based on the NCERT textbook, offering clear, step-by-step explanations to make complex problems easier to understand. With these easy solutions, students can confidently approach and solve various types of linear equations, strengthening their algebraic problem-solving abilities.
Class 8 Maths Exercise 2.6 Easy Solutions NCERT
Solve the following equations.
Ex 2.6 Class 8 Maths Question 1.
(8x-3 )/3x =2
Solution:
We have (8x-3 )/3x=2
⇒ ( 8x-3 )/3x = 2 / 1
⇒ 8x – 3 = 2 × 3x (Cross-multiplication)
⇒ 8x – 3 = 6x
⇒ 8x – 6x = 3 (Transposing 6x to LHS and 3 to RHS)
⇒ 2x = 3
⇒ x = 3/2
Ex 2.6 Class 8 Maths Question 2.
9x /(7-6x ) = 15
Solution:
we have 9x /(7-6x } = 15
⇒ 9x/(7-6x ) = 15 /1
⇒ 9x = 15(7 – 6x) (Cross-multiplication)
⇒ 9x = 105 – 90x (Solving the bracket)
⇒ 9x + 90x = 105 (Transposing 90x to LHS)
⇒ 99x = 105
⇒ x = \frac { 105 }{ 99 }
⇒ x = \frac { 35 }{ 33 }
Ex 2.6 Class 8 Maths Question 3.
\frac { z }{ z+15 } =\frac { 4 }{ 9 }
Solution:
We have \frac { z }{ z+15 } =\frac { 4 }{ 9 }
⇒ 9z = 4 (z + 15) (Cross-multiplication)
⇒ 9z = 4z + 60 (Solving the bracket)
⇒ 9z – 42 = 60
⇒ 5z = 60
⇒ z = 12
Ex 2.6 Class 8 Maths Question 4.
\frac { 3y+4 }{ 2-6y } =\frac { -2 }{ 5 }
Solution:
we have \frac { 3y+4 }{ 2-6y } =\frac { -2 }{ 5 }
⇒ 5(3y + 4) = -2(2 – 6y) (Cross-multiplication)
⇒ 15y + 20 = -4 + 12y (Solving the bracket)
⇒ 15y – 12y = -4 – 20 (Transposing 12y to LHS and 20 to RHS)
⇒ 3y = -24 (Transposing 3 to RHS) -24
⇒ y = -8
Ex 2.6 Class 8 Maths Question 5.
\frac { 7y+4 }{ y+2 } =\frac { -4 }{ 3 }
Solution:
we have \frac { 7y+4 }{ y+2 } =\frac { -4 }{ 3 }
⇒ 3(7y + 4) = -4 (y + 2) (Corss-multiplication)
⇒ 21y + 12 = -4y – 8 [Solving the bracket]
⇒ 21y + 4y = -12 – 8 [Transposing 4y to LHS and 12 to RHS]
⇒ 25y = -20 [Transposing 25 to RHS]
⇒ y = \frac { -4 }{ 5 }
Ex 2.6 Class 8 Maths Question 6.
The ages of Hari and Harry are in the ratio 5 : 7. Four years from now the ratio of their ages will be 3 : 4. Find their present ages.
Solution:
Let the present ages of Hari and Harry be 5x years and 7x years respectively.
After 4 years Hari’s age will be (5x + 4) years and Harry’s age will be (7x + 4) years.
As per the conditions, we have
\frac { 5x+4 }{ 7x+4 } =\frac { 3 }{ 4 }
⇒ 4(5x + 4) = 3(7x + 4) (Cross-multiplication)
⇒ 20x + 16 = 21x + 12 (Solving the bracket)
⇒ 20x – 21x = 12 – 16 (Transposing 21x to LHS and 16 to RHS)
⇒ -x = -4
⇒ x = 4
Hence the present ages of Hari and Harry are 5 × 4 = 20years and 7 × 4 = 28years respectively.
Ex 2.6 Class 8 Maths Question 7.
The denominator of a rational number is greater than its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, the number obtained is \frac { 3 }{ 2 }. Find the rational number.
Solution:
Let the numerator of the rational number be x.
Denominator = (x + 8)
As per the conditions, we have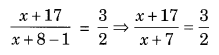
⇒ 2(x + 17) = 3(x + 7) (Cross-multiplication)
⇒ 2x + 34 = 3x + 21 (Solving the bracket)
⇒ 2x – 3x = 21 – 34 (Transposing 3x to LHS and 34 to RHS)
⇒ -x = -13
⇒ x = 13
Thus, numerator = 13
and denominator = 13 + 8 = 21
Hence the rational number is \frac { 13 }{ 21 }.
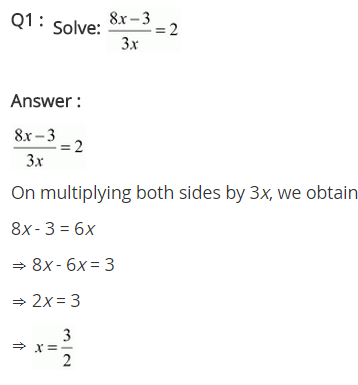



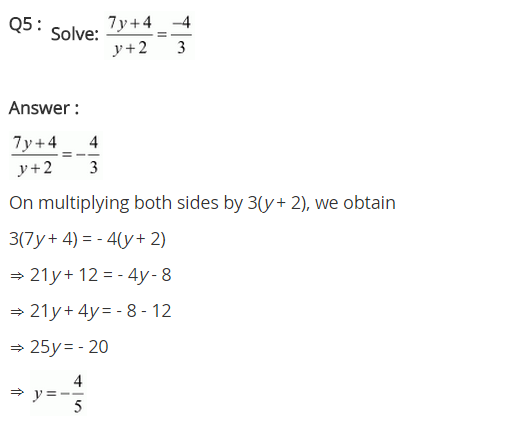


📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
https://ncert.nic.in/textbook.php?class=10
