Class 8 Maths Exercise 3.2 Easy Solutions NCERT focuses on understanding the properties of quadrilaterals. In this exercise, students learn to identify and work with different types of quadrilaterals, such as parallelograms, rectangles, and squares, by applying key concepts. The easy, step-by-step solutions provided are based on the NCERT textbook, offering clear and simple explanations to help you grasp the concepts better. With these solutions, you’ll be able to solve problems involving angles, sides, and properties of various quadrilaterals with confidence.
Class 8 Maths Exercise 3.2 Easy Solutions NCERT
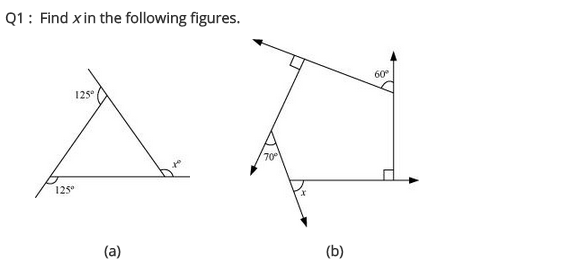
Ex 3.2 Class 8 Maths Question 1.
Find x in the following figures.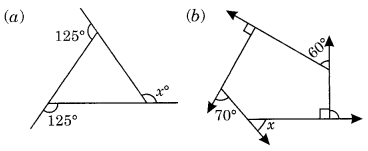
Solution:
(a) We know that the sum of all the exterior angles of a polygon = 360°
125° + 125° + x = 360°
⇒ 250° + x = 360°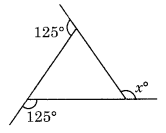
x = 360° – 250° = 110°
Math educational software
NCERT Books
Hence x = 110°
(b) Here ∠y = 180° – 90° = 90°
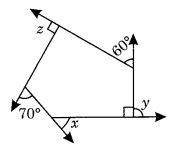
and ∠z = 90° (given)
x + y + 60° + z + 70° = 360° [∵ Sum of all the exterior angles of a polygon = 360°]
⇒ x + 90° + 60° + 90° + 70° = 360°
⇒ x + 310° = 360°
⇒ x = 360° – 310° = 50°
Hence x = 50°
Ex 3.2 Class 8 Maths Question 2.
Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides
Solution:
(i) We know the sum of all the exterior angles of polygon = 360°
Measure of each angle of 9 sided regular polygon = 3609 = 40°
(ii) Sum of all the exterior angles of a polygon = 360°
Measure of each angle of 15 sided regular polygon = 36015 = 24°
Ex 3.2 Class 8 Maths Question 3.
How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Solution:
Sum of all exterior angles of a regular polygon = 360°
Number of sides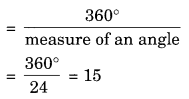
Hence, the number of sides = 15
Ex 3.2 Class 8 Maths Question 4.
How many sides does a regular polygon have if each of its interior angles is 165°?
Solution:
Let re be the number of sides of a regular polygon.
Sum of all interior angles = (n – 2) × 180°
and, measure of its each angle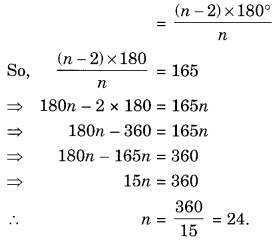
Hence, the number of sides = 24
Ex 3.2 Class 8 Maths Question 5.
(a) Is it possible to have a regular polygon with measure of each exterior angle a is 22°?

not a whole number.
Since number of sides cannot be in fractions.
It is not possible for a regular polygon to have its interior angle = 22°.
Ex 3.2 Class 8 Maths Question 6.
(a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Solution:
(a) Sum of all interior angles of a regular polygon of side n = (n – 2) × 180°
The measure of each interior angle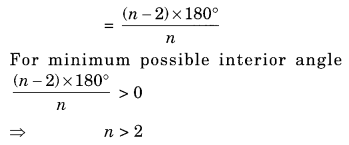
The minimum measure the angle of an equilateral triangle (n = 3) = 60°.
(b) From part (a) we can conclude that the maximum exterior angle of a regular polygon = 180° – 60° = 120°.


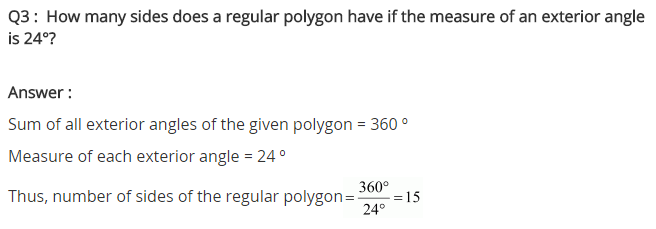



📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
https://ncert.nic.in/textbook.php?class=10
