Class 8 Maths Exercise 3.3 Easy Solutions NCERT continues the exploration of quadrilaterals, focusing on their properties and how to solve related problems. This exercise includes questions on identifying and calculating angles, sides, and diagonals of various quadrilaterals. The step-by-step solutions are based on the NCERT textbook, designed to make complex concepts easier to understand. With clear and simple explanations, students can confidently work through each problem and deepen their understanding of quadrilaterals and their properties.
Class 8 Maths Exercise 3.3 Easy Solutions NCERT
Ex 3.3 Class 8 Maths Question 1.
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD = …………
(ii) ∠DCB = ………
(iii) OC = ………
(iv) m∠DAB + m∠CDA = ……..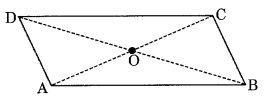
Solution:
(i) AD = BC [Opposite sides of a parallelogram are equal]
NCERT Books
Mathematics textbooks
(ii) ∠DCB = ∠DAB [Opposite angles of a parallelogram are equal]
(iii) OC = OA [Diagonals of a parallelogram bisect each other]
(iv) m∠DAB + m∠CDA = 180° [Adjacent angles of a parallelogram are supplementary]
Ex 3.3 Class 8 Maths Question 2.
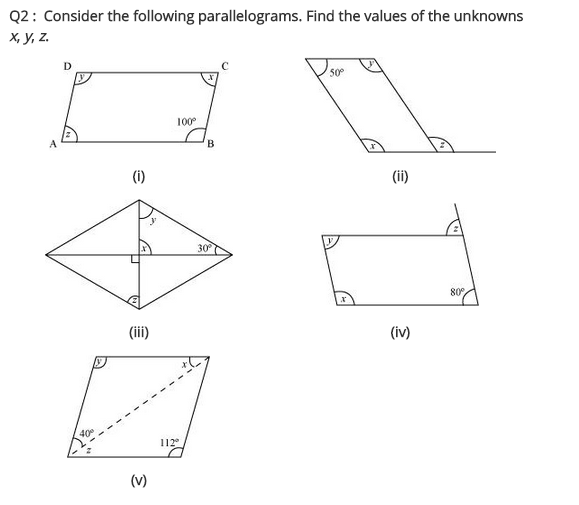
Consider the following parallelograms. Find the values of the unknowns x, y, z.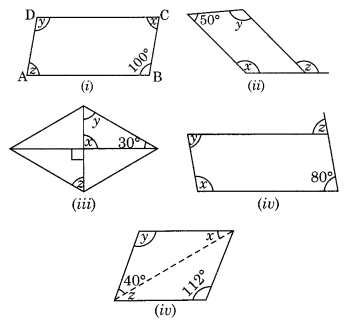
Solution:
(i) ABCD is a parallelogram.
∠B = ∠D [Opposite angles of a parallelogram are equal]
∠D = 100°
⇒ y = 100°
∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]
⇒ z + 100° = 180°
⇒ z = 180° – 100° = 80°
∠A = ∠C [Opposite angles of a ||gm]
x = 80°
Hence x = 80°, y = 100° and z = 80°
(ii) PQRS is a parallelogram.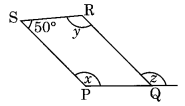
∠P + ∠S = 180° [Adjacent angles of parallelogram]
⇒ x + 50° = 180°
x = 180° – 50° = 130°
Now, ∠P = ∠R [Opposite angles are equal]
⇒ x = y
⇒ y = 130°
Also, y = z [Alternate angles]
z = 130°
Hence, x = 130°, y = 130° and z = 130°
(iii) ABCD is a rhombus.
[∵ Diagonals intersect at 90°]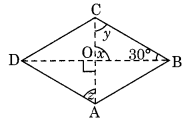
x = 90°
Now in ∆OCB,
x + y + 30° = 180° (Angle sum property)
⇒ 90° + y + 30° = 180°
⇒ y + 120° = 180°
⇒ y = 180° – 120° = 60°
y = z (Alternate angles)
⇒ z = 60°
Hence, x = 90°, y = 60° and z = 60°.
(iv) ABCD is a parallelogram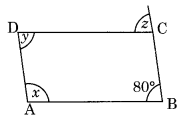
∠A + ∠B = 180° (Adjacent angles of a parallelogram are supplementary)
⇒ x + 80° = 180°
⇒ x = 180° – 80° = 100°
Now, ∠D = ∠B [Opposite angles of a |jgm]
⇒ y = 80°
Also, z = ∠B = 80° (Alternate angles)
Hence x = 100°, y = 80° and z = 80°
(v) ABCD is a parallelogram.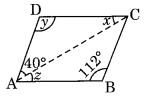
∠D = ∠B [Opposite angles of a ||gm]
y = 112°
x + y + 40° = 180° [Angle sum property]
⇒ x + 112° + 40° = 180°
⇒ x + 152° = 180°
⇒ x = 180° – 152 = 28°
z = x = 28° (Alternate angles)
Hence x = 28°, y = 112°, z = 28°.
Ex 3.3 Class 8 Maths Question 3.
Can a quadrilateral ABCD be a parallelogram if
(i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii) ∠A = 70° and ∠C = 65°?
Solution:
(i) For ∠D + ∠B = 180, quadrilateral ABCD may be a parallelogram if following conditions are also fulfilled.
(a) The sum of measures of adjacent angles should be 180°.
(b) Opposite angles should also be of same measures. So, ABCD can be but need not be a parallelogram.
(ii) Given: AB = DC = 8 cm, AD = 4 cm, BC = 4.4 cm
In a parallelogram, opposite sides are equal.
Here AD ≠ BC
Thus, ABCD cannot be a parallelogram.
(iii) ∠A = 70° and ∠C = 65°
Since ∠A ≠ ∠C
Opposite angles of quadrilateral are not equal.
Hence, ABCD is not a parallelogram.
Ex 3.3 Class 8 Maths Question 4.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Solution:
ABCD is a rough figure of a quadrilateral in which m∠A = m∠C but it is not a parallelogram. It is a kite.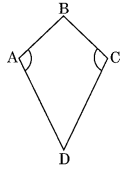
Ex 3.3 Class 8 Maths Question 5.
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Solution:
Let ABCD is parallelogram such that
m∠B : m∠C = 3 : 2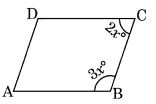
Let m∠B = 3x° and m∠C = 2x°
m∠B + m∠C = 180° (Sum of adjacent angles = 180°)
3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
Thus, ∠B = 3 × 36 = 108°
∠C = 2 × 36° = 72°
∠B = ∠D = 108°
and ∠A = ∠C = 72°
Hence, the measures of the angles of the parallelogram are 108°, 72°, 108° and 72°.
Ex 3.3 Class 8 Maths Question 6.
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Solution:
Let ABCD be a parallelogram in which
∠A = ∠B
We know ∠A + ∠B = 180° [Sum of adjacent angles = 180°]
∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
Thus, ∠A = ∠C = 90° and ∠B = ∠D = 90°
[Opposite angles of a parallelogram are equal]
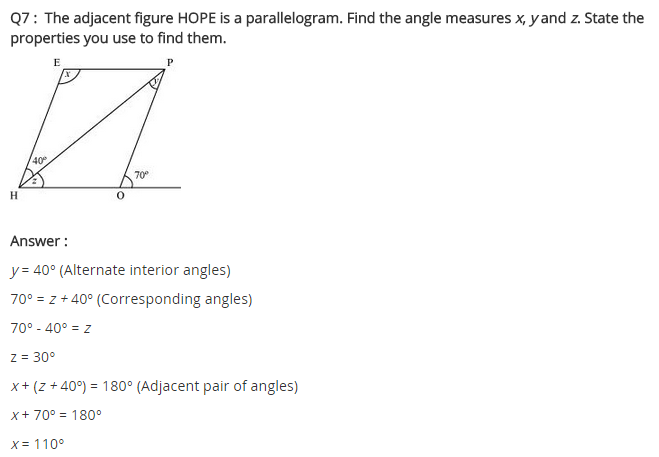
Ex 3.3 Class 8 Maths Question 7.
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.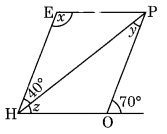
Solution:
∠y = 40° (Alternate angles)
∠z + 40° = 70° (Exterior angle property)
⇒ ∠z = 70° – 40° = 30°
z = ∠EPH (Alternate angle)
In ∆EPH
∠x + 40° + ∠z = 180° (Adjacent angles)
⇒ ∠x + 40° + 30° = 180°
⇒ ∠x + 70° = 180°
⇒ ∠x = 180° – 70° = 110°
Hence x = 110°, y = 40° and z = 30°.
Ex 3.3 Class 8 Maths Question 8.
The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)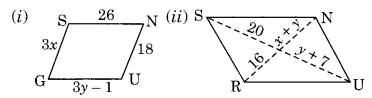
Solution:
(i) GU = SN (Opposite sides of a parallelogram)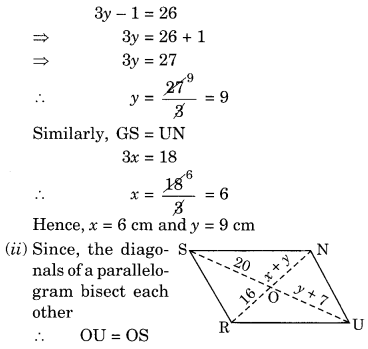
⇒ y + 7 = 20
⇒ y = 20 – 7 = 13
Also, ON = OR
⇒ x + y = 16
⇒ x + 13 = 16
x = 16 – 13 = 3
Hence, x = 3 cm and y = 13 cm.
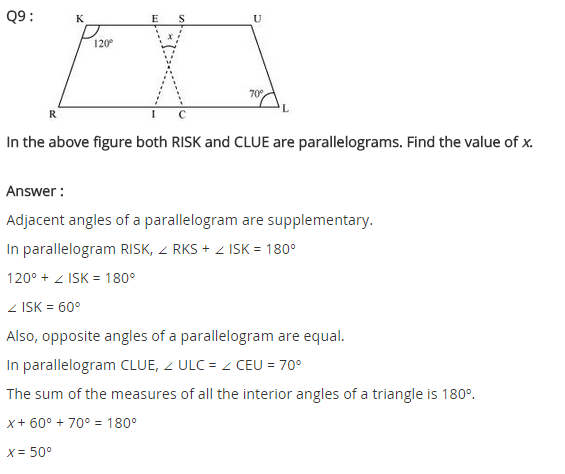
Ex 3.3 Class 8 Maths Question 9.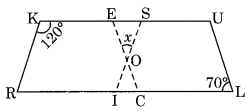
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Solution:
Here RISK and CLUE are two parallelograms.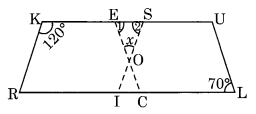
∠1 = ∠L = 70° (Opposite angles of a parallelogram)
∠K + ∠2 = 180°
Sum of adjacent angles is 180°
120° + ∠2 = 180°
∠2 = 180° – 120° = 60°
In ∆OES,
∠x + ∠1 + ∠2 = 180° (Angle sum property)
⇒ ∠x + 70° + 60° = 180°
⇒ ∠x + 130° = 180°
⇒ ∠x = 180° – 130° = 50°
Hence x = 50°
Ex 3.3 Class 8 Maths Question 10.
Explain how this figure is a trapezium. Which of its two sides are parallel?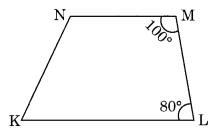
Solution:
∠M + ∠L = 100° + 80° = 180°
∠M and ∠L are the adjacent angles, and sum of adjacent interior angles is 180°
KL is parallel to NM
Hence KLMN is a trapezium.
Ex 3.3 Class 8 Maths Question 11.
Find m∠C in below figure if AB¯ || DC¯
Solution:
Given that AB¯ || DC¯
m∠B + m∠C = 180° (Sum of adjacent angles of a parallelogram is 180°)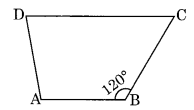
120° + m∠C = 180°
m∠C = 180° – 120° = 60°
Hence m∠C = 60°
Ex 3.3 Class 8 Maths Question 12.
Find the measure of ∠P and ∠S if SP¯ || RQ¯ in figure, is there any other method to find m∠P?)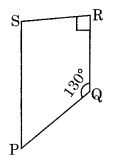
Solution:
Given that ∠Q = 130° and ∠R = 90°
SP¯ || RQ¯ (given)
∠P + ∠Q = 180° (Adjacent angles)
⇒ ∠P + 130° = 180°
⇒ ∠P = 180° – 130° = 50°
and, ∠S + ∠R = 180° (Adjacent angles)
⇒ ∠S + 90° = 180°
⇒ ∠S = 180° – 90° = 90°
Alternate Method:
∠Q = 130°, ∠R = 90° and ∠S = 90°
We know that
∠P + ∠Q + ∠R + ∠Q = 360° (Angle sum property of quadrilateral)
⇒ ∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°
⇒ ∠P = 360° – 310° = 50°
Hence m∠P = 50°









📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
https://ncert.nic.in/textbook.php?class=10
