Class 8 Maths Exercise 8.3 Easy Solutions NCERT introduces the concept of compound interest and how it differs from simple interest. This exercise helps students understand the formula and method to calculate compound interest for different time periods. The step-by-step NCERT-based solutions provided here make these calculations easy to follow and apply. With clear explanations and solved examples, students can confidently learn and practice compound interest problems.
Class 8 Maths Exercise 8.3 Easy Solutions NCERT
Ex 8.3 Class 8 Maths Question 1.
Calculate the amount and compound interest on
(a) ₹ 10,800 for 3 years at 1212 % per annum compounded annually.
(b) ₹ 18,000 for 212 years at 10% per annum compounded annually.
(c) ₹ 62,500 for 112 years at 8% per annum compounded half yearly.
(d) ₹ 8,000 for 1 year at 9% per annum compounded half yearly. (You could use the year by year calculation using SI formula to verify).
(e) ₹ 10,000 for 1 year at 8% per annum compounded half yearly.
Solution:
(a) Given:
P = ₹ 10,800, n = 3 years,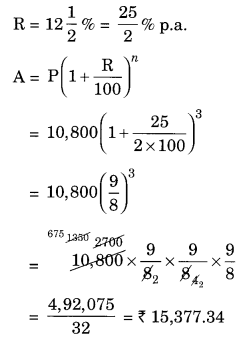
NCERT Books
CI = A – P = ₹ 15,377.35 – ₹ 10,800 = ₹ 4,577.35
Hence amount = ₹ 15,377.34 and CI = ₹ 4,577.34
(b) Given: P = ₹ 18,000, n = 212 years = 52 years
R = 10% p.a.
The amount for 212 years, i.e., 2 years and 6 months can be calculated by first calculating the amount to 2 years using CI formula and then calculating the simple interest by using SI formula.
The amount for 2 years has to be calculated

Total CI = ₹ 3780 + ₹ 1089 = ₹ 4,869
Amount = P + I = ₹ 21,780 + ₹ 1,089 = ₹ 22,869
Hence, the amount = ₹ 22,869
and CI = ₹ 4,869
(c) Given: P = ₹ 62,500, n = 112 years = 32 years per annum compounded half yearly
= 32 × 2 years = 3 half years
R = 8% = 82 % = 4% half yearly
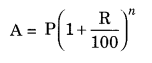
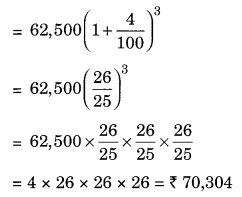
CI = A – P = ₹ 70,304 – ₹ 62,500 = ₹ 7,804
Hence, amount = ₹ 70304 and CI = ₹ 7804
(d) Given: P = ₹ 8,000, n = 1 years R = 9% per annum compounded half yearly
Since, the interest is compounded half yearly n = 1 × 2 = 2 half years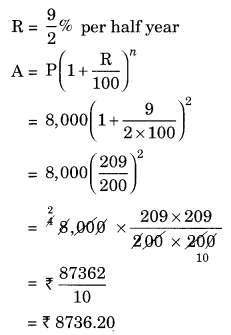
CI = A – P = ₹ 8,736.20 – ₹ 8,000 = ₹ 736.20
Hence, the amount = ₹ 8736.20 and CI = ₹ 736.20
(e) Given: P = ₹ 10,000, n = 1 year and R = 8% pa compounded half yearly
Since the interest is compounded half yearly n = 1 × 2 = 2 half years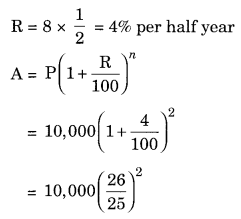
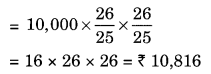
CI = A – P = ₹ 10,816 – ₹ 10,000 = ₹ 816
Hence the amount = ₹ 10,816 and Cl = ₹ 816
Ex 8.3 Class 8 Maths Question 2.
Kamala borrowed ₹ 26,400 from a Bank to buy a scooter at a rate of 15% per annum compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan? (Hint: Find amount for 2 years with interest is compounded yearly and then find SI on the 2nd
year amount for 412 years).
Solution:
Given:
P = ₹ 26,400
R = 15% p.a. compounded yearly
n = 2 years and 4 months
Amount after 2 years and 4 months = ₹ 34,914 + ₹ 1745.70 = ₹ 36,659.70
Hence, the amount to be paid by Kamla = ₹ 36,659.70
Ex 8.3 Class 8 Maths Question 3.
Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
For Fabina: P = ₹ 12,500, R = 12% p.a. and n = 3 years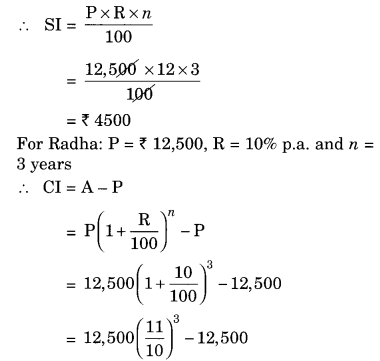

Difference between the two interests = ₹ 4500 – ₹ 4137.50 = ₹ 362.50
Hence, Fabina pays more interest by ₹ 362.50.
Ex 8.3 Class 8 Maths Question 4.
I borrowed ₹ 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
Given: P = ₹ 12,000, R = 6% p.a., n = 2 years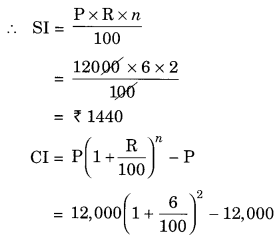

Difference between two interests = ₹ 1483.20 – ₹ 1440 = ₹ 43.20
Hence, the extra amount to be paid = ₹ 43.20
Ex 8.3 Class 8 Maths Question 5.
Vasudevan invested ₹ 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?
Solution:
(i) Given: P = ₹ 60,000, R = 12% p.a. compounded half yearly
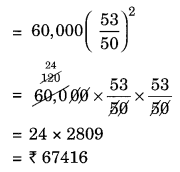
Hence, the required amount = ₹ 67416
Ex 8.3 Class 8 Maths Question 6.
Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after
112 years if the interest is
(i) compounded annually.
(ii) compounded half yearly.
Solution:
(i) Given: P = ₹ 80,000
R = 10% p.a.
n = 112 years
Since the interest is compounded annually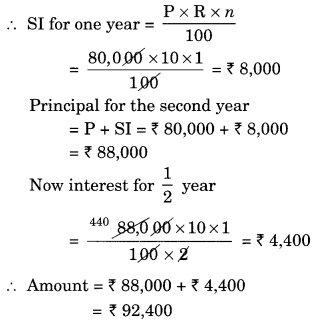
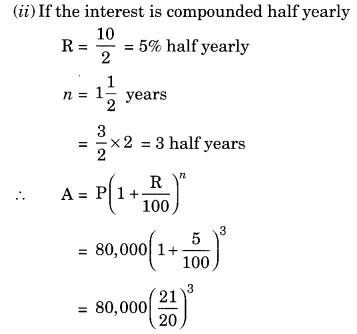
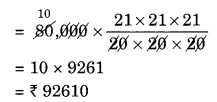
Difference between the amounts = ₹ 92,610 – ₹ 92,400 = ₹ 210
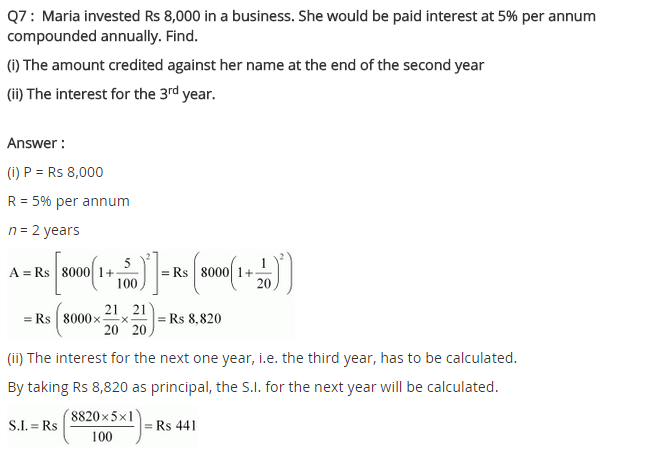
Ex 8.3 Class 8 Maths Question 7.
Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(i) The amount credited against her name at the end of the second year.
(ii) The interest for the third year.
Solution:
(i) Given: P = ₹ 8,000, R = 5% p.a.
and n = 2 years
Hence, interest for the third year = ₹ 441
Ex 8.3 Class 8 Maths Question 8.
Find the amount and the compound interest on ₹ 10,000 for 112 years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution:
Given: P = ₹ 10,000, n = 112 years
R = 10% per annum
Since the interest is compounded half yearly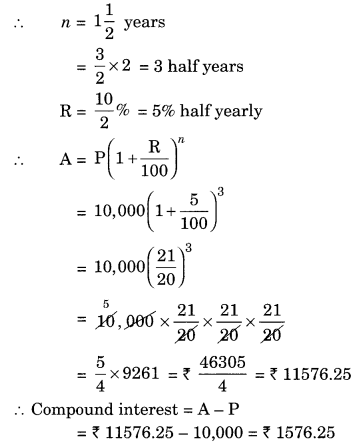

Total interest = ₹ 1,000 + ₹ 550 = ₹ 1,550
Difference between the two interests = ₹ 1,576.25 – ₹ 1,550 = ₹ 26.25
Hence, the interest will be ₹ 26.25 more when compounded half yearly than the interest when compounded annually.
Ex 8.3 Class 8 Maths Question 9.
Find the amount which Ram will get on ₹ 4,096, if he gave it for 18 months at 1212 per annum, interest being compounded half yearly.
Solution:
Given: P = ₹ 4,096, R = 1212 % pa, n = 18 months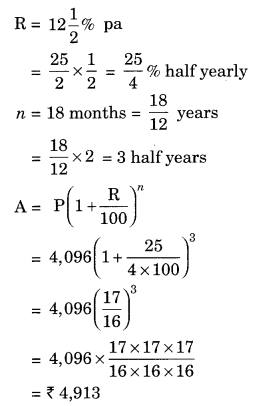
Hence, the required amount = ₹ 4913
Ex 8.3 Class 8 Maths Question 10.
The population of a place increased to 54,000 in 2003 at a rate of 5% per annum.
(i) Find the population in 2001.
(ii) What would be its population in 2005?
Solution:
(i) Given: Population in 2003 = 54,000
Rate = 5% pa
Time = 2003 – 2001 = 2 years
Population in 2003 = Population in 2001
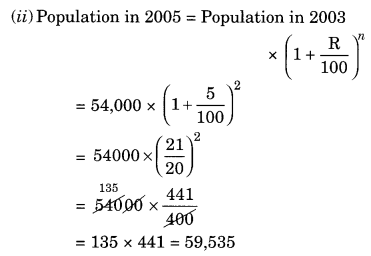
Ex 8.3 Class 8 Maths Question 11.
In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
Given: Initial count of bacteria = 5,06,000
Rate = 2.5% per hour
n = 2 hours
Number of bacteria at the end of 2 hours = Number of count of bacteria initially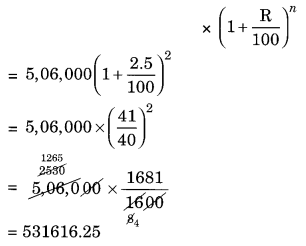
Thus, the number of bacteria after two hours = 5,31,616 (approx).
Ex 8.3 Class 8 Maths Question 12.
A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
Given: Cost price of the scooter = ₹ 42,000
Rate of depreciation = 8% p.a.
Time = 1 year
Final value of the scooter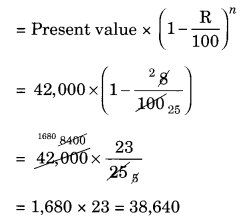
Hence, the value of scooter after 1 year = ₹ 38,640.



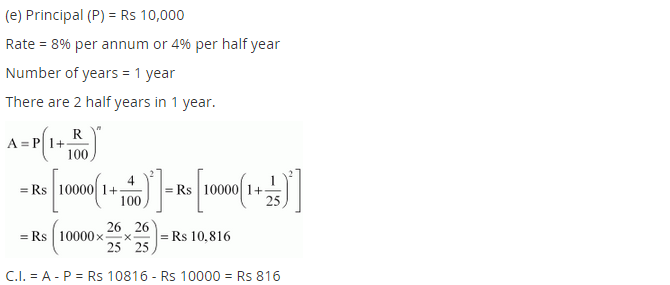





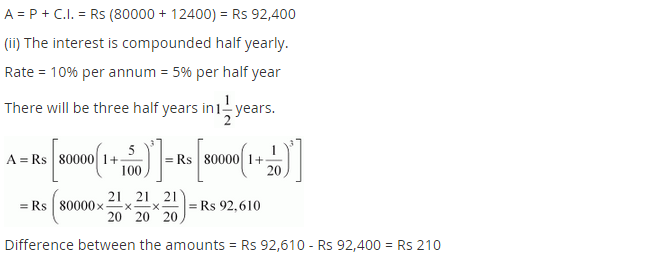




📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
https://ncert.nic.in/textbook.php?class=10
