Laws of Motion high school physics is one of the most important chapters for understanding how forces affect motion. In NCERT Class 11 Physics, this topic covers Newton’s three laws, the law of inertia, force and momentum, friction, equilibrium, and circular motion. Whether you are a Grade 11 student following NCERT or a high school learner studying physics worldwide, the laws of motion provide the foundation for solving real-life problems – from a car taking a turn to a satellite moving around Earth.
On this page, you will find clear explanations, solved examples, NCERT Class 11 exercises, and key formulas to make learning the laws of motion in high school physics simple and effective
This makes the chapter easier to understand for both Grade 11 NCERT students and other high school learners around the world.
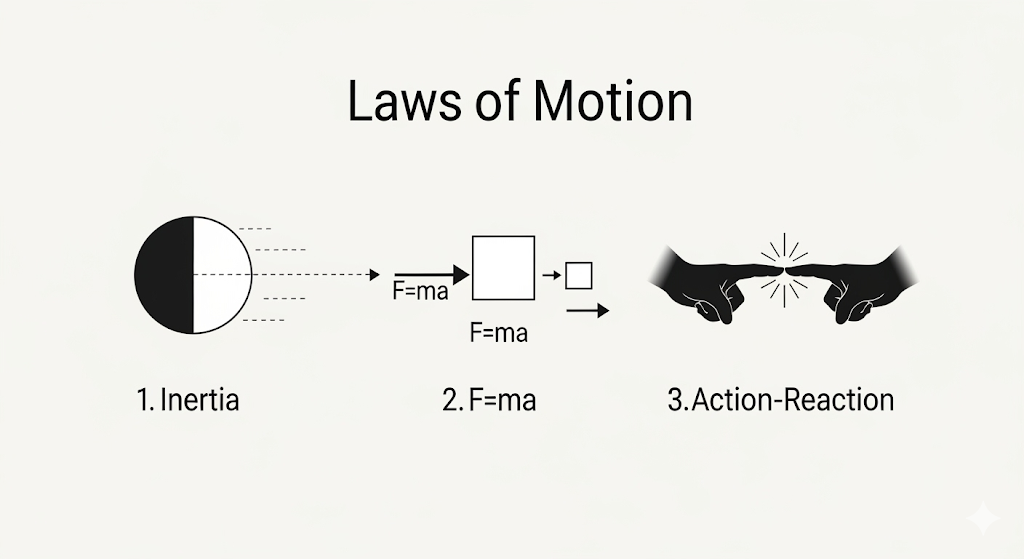

Laws of motion high school physics – Full Concept
Part 1: Introduction, Inertia, and Newton’s First Law
In high school physics and specifically in NCERT Class 11 Physics, the chapter “Laws of Motion” introduces these concepts step by step. This chapter is not only important for exams but also for building strong fundamentals in science. If you understand the laws of motion, you can easily solve problems in mechanics, learn about circular motion, gravitation, work, energy, and even advanced topics like fluid mechanics and oscillations later.
Aristotle’s Idea and Why It Was Wrong
Before Newton, people believed in the ideas of the Greek philosopher Aristotle. He said that a force is always required to keep an object in motion.

For example, if you throw a ball, it eventually stops. Aristotle thought that this happens because continuous force is needed to keep it moving.
But this is not true. The ball stops because of friction and air resistance, not because motion naturally dies away. If friction and resistance were absent, the ball would keep moving forever.
So, Aristotle’s explanation was not correct. It took many centuries for scientists to realize the actual truth about motion.
Galileo’s Contribution – The Law of Inertia
The Italian scientist Galileo Galilei studied motion carefully. He performed experiments with inclined planes. He observed that when a ball rolls down a slope, it gains speed. When it rolls up a slope, it slows down. On a perfectly horizontal, smooth surface, the ball continues to move with the same speed without stopping.
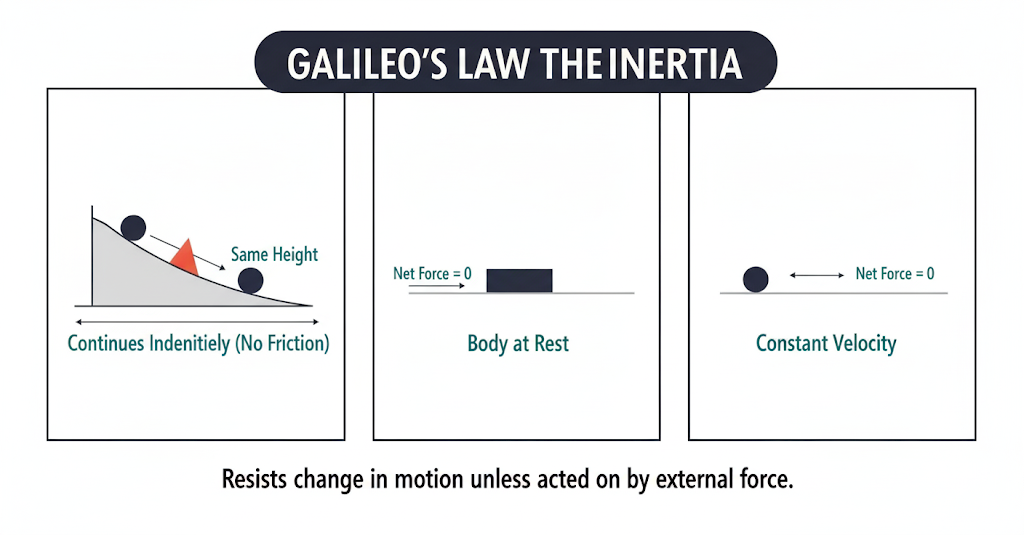
From this, Galileo concluded that:
This natural tendency of objects to resist a change in their state of motion is called inertia.
An object will continue in its state of rest or uniform motion unless some external force changes it.
Types of Inertia
Inertia of Rest – A body at rest stays at rest unless a force makes it move.
Example: When a bus suddenly starts, passengers feel a backward jerk because their bodies tend to remain at rest.
Inertia of Motion – A moving body continues to move unless a force stops it.
Example: When a bus suddenly stops, passengers are thrown forward because their bodies tend to remain in motion.
Inertia of Direction – A body moving in one direction tends to keep moving in the same direction.
Example: When a car takes a sharp turn, passengers feel a sideways push because their bodies resist the change in direction.
Newton’s First Law of Motion
Building on Galileo’s ideas, Sir Isaac Newton gave the three laws of motion. The first one is called the Law of Inertia.
Statement:
A body continues to be in its state of rest or uniform motion in a straight line unless compelled to change that state by an external force.
This means:
If no external force acts on a body, then a stationary object remains stationary, and a moving object keeps moving with constant velocity in a straight line.
An external force is necessary to change the state of motion (speed or direction) of an object.
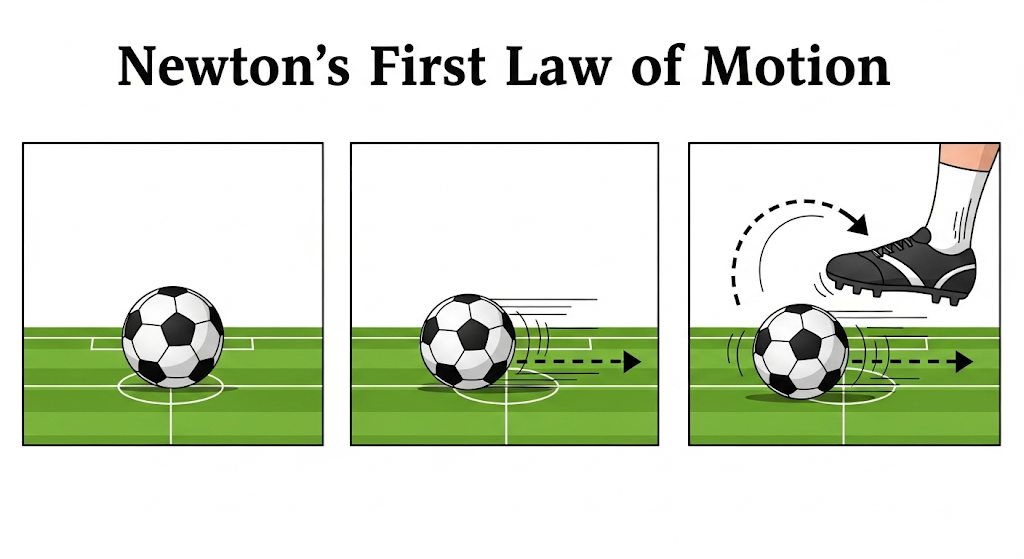
Examples of Newton’s First Law
In space, a satellite keeps moving around the Earth without any engine running, because no force is opposing its motion.
A book lying on a table will stay at rest until someone applies force to move it.
A ball rolling on a frictionless surface will never stop by itself; it will keep moving.
Importance of Newton’s First Law
It clearly explains why forces are required not to maintain motion, but to change motion.
It gives the concept of inertia, which is fundamental to understanding mechanics.
It connects directly to real-life situations like driving, sports, and safety (e.g., seatbelts in cars prevent passengers from moving forward suddenly due to inertia).
Newton’s Second Law of Motion
Newton’s First Law explains the concept of inertia but does not tell us what happens when a force is actually applied. To answer this, Newton gave his Second Law of Motion.
Statement: The rate of change of momentum of a body is directly proportional to the applied force and takes place in the direction of the force.
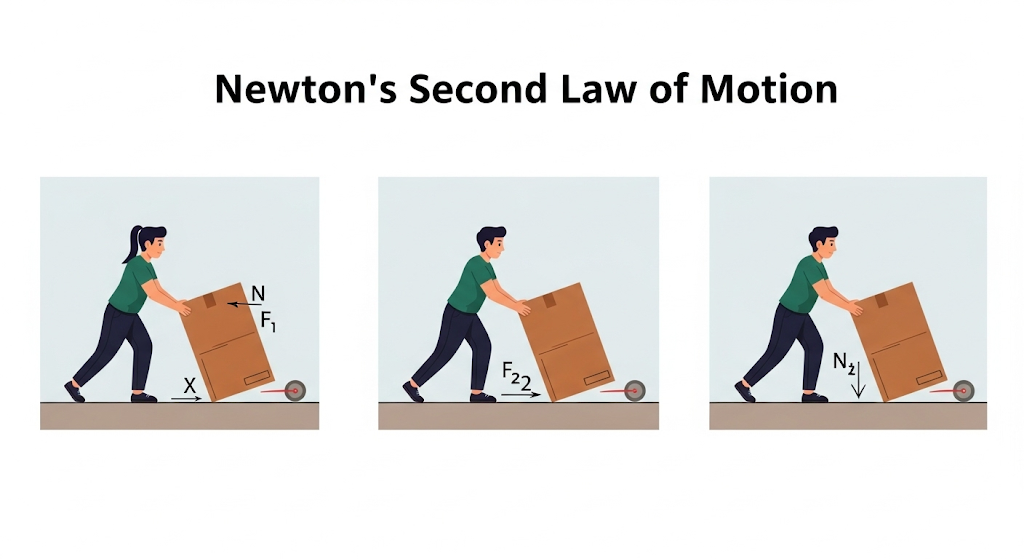
This law shows the exact relationship between force, mass, and acceleration. It tells us how much acceleration will be produced in a body when a force is applied.
Momentum
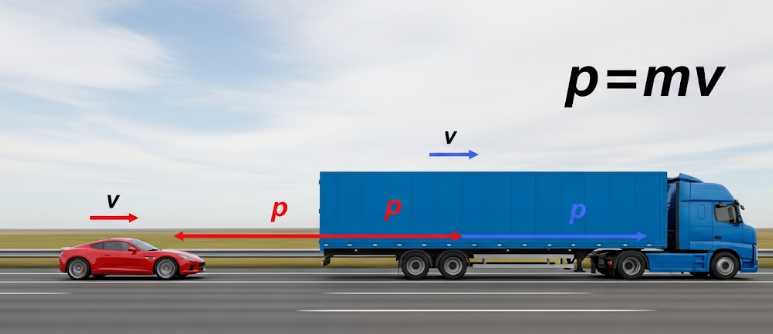
Before using the Second Law, we need to understand momentum.
Momentum (p) is defined as the product of mass and velocity:
p = m × v
It is a vector quantity, which means it has both magnitude and direction.
SI unit: kg·m/s
Derivation of F = ma – Laws of motion high school physics
According to Newton’s Second Law of Motion, the force acting on a body is equal to the rate of change of its momentum.
Momentum (p) of a body is given by:
p = m × v
where m = mass of the body, v = velocity of the body.

Now, Force ∝ rate of change of momentum:
F ∝ dp/dt
If the mass is constant,
dp/dt = m × dv/dt
But, dv/dt = a (acceleration)
So, dp/dt = m × a
Therefore, F ∝ m a
By choosing proper units, the proportionality becomes equality:
F = m a
Understanding the Law Through Examples
Pushing a bicycle vs. a car: A bicycle accelerates easily because its mass is small. A car hardly moves with the same push because its mass is large.
Cricket ball and catching: A fast-moving ball has high momentum. The fielder must apply a large force to stop it.
Hammer and nail: A hammer has large mass and velocity. It can drive a nail into wood because of its high momentum.
Impulse
Sometimes a force acts for a very short time. In such cases, we use the concept of impulse. Impulse (J) = Force × Time = Change in Momentum
SI unit: Newton-second (N·s)

Examples: (i) Airbags in cars increase the time of collision, reducing the force on passengers. (ii) A footballer kicks a ball: contact time is very small, but the force is large, producing a large impulse.
A boxer delivers a quick punch, transferring momentum in a very short time.
Applications of Second Law and Impulse
Sports: Cricketers and goalkeepers move their hands backward while catching to increase the time of contact and reduce the force.
Safety: Seat belts and airbags increase stopping time, lowering the force on passengers during accidents.
Engineering: Heavy hammers with large momentum are used to drive poles into the ground.
Everyday life: It is easier to stop a slow ball (low momentum) than a fast one (high momentum).
Solved Example 1 – Momentum
Q: A ball of mass 0.05 kg is thrown with a velocity of 20 m/s. What is its momentum?
Solution: p = m × v = 0.05 × 20 = 1.0 kg·m/s
So, the momentum is 1.0 kg·m/s.
Newton’s Third Law of Motion
Newton’s Third Law is one of the most famous principles in physics.
Statement: For every action, there is an equal and opposite reaction.
This means: If object A exerts a force on object B, then object B exerts an equal but opposite force on object A. These two forces always occur in pairs and act on different bodies.

Examples of Newton’s Third Law When you jump off a small boat, the boat moves backward as you move forward.
When you walk, your foot pushes the ground backward (action), and the ground pushes your foot forward (reaction).
A gun recoils backward when a bullet is fired forward.
When a swimmer pushes water backward, the water pushes the swimmer forward.
Conservation of Momentum
Newton’s Third Law leads to the principle of conservation of momentum.
Law: The total momentum of a system of interacting bodies remains constant if no external force acts on the system.
In other words, momentum is neither created nor destroyed. It only transfers from one body to another.
Derivation of Conservation of Momentum
According to Newton’s Third Law of Motion, every action has an equal and opposite reaction. This principle leads directly to the law of conservation of momentum.
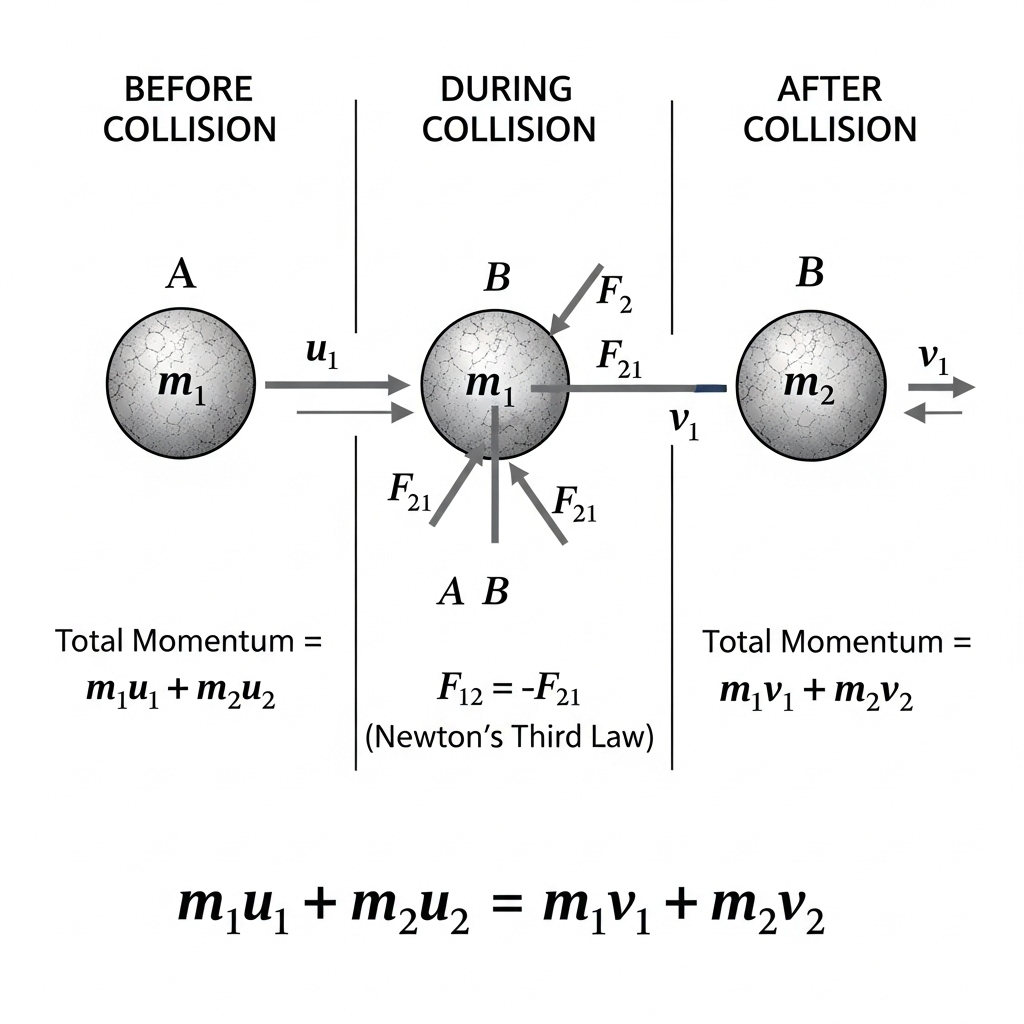
Consider two bodies, A and B, colliding with each other. At the same time, body B exerts an equal and opposite force –F on body A.
Mass of body A = m₁, initial velocity = u₁, final velocity = v₁ Mass of body B = m₂, initial velocity = u₂, final velocity = v₂
During collision, body A exerts a force F on body B.
From Newton’s Second Law:
Force = rate of change of momentum
For body A:
F = (m₁v₁ – m₁u₁) / t
For body B:
–F = (m₂v₂ – m₂u₂) / t
Adding the two equations:
F + (–F) = [(m₁v₁ – m₁u₁) + (m₂v₂ – m₂u₂)] / t
0 = (m₁v₁ + m₂v₂) – (m₁u₁ + m₂u₂)
Therefore,
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
Total momentum before collision = Total momentum after collision
Hence, momentum is conserved if no external force acts on the system.
Applications of Conservation of Momentum
Gun and Bullet: When a bullet is fired, the gun recoils so that the total momentum of the system remains zero.
Rocket Propulsion: Hot gases are expelled backward at high speed, and the rocket moves forward.
Collisions of Vehicles: Momentum before and after a collision is conserved if external forces are negligible.
Fireworks: When a cracker explodes, fragments move in different directions but the total momentum remains conserved.
Friction
Friction is the force that opposes the relative motion between two surfaces in contact. It arises due to irregularities on surfaces and intermolecular forces.
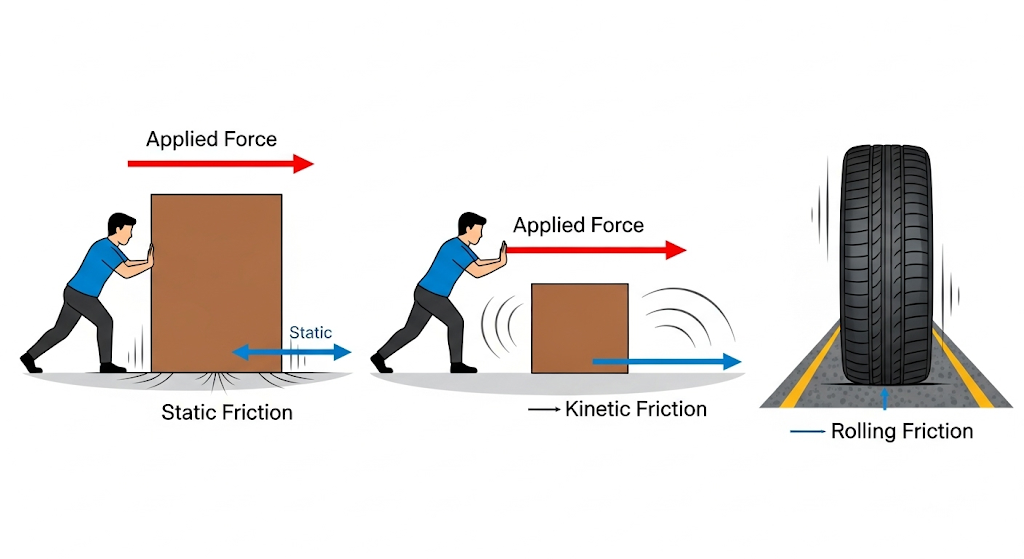
Types of Friction
Rolling Friction – The resistance offered when a body rolls over a surface. It is smaller than sliding friction.
Static Friction – The force that prevents a body from starting to move. It adjusts itself to balance the applied force up to a maximum limit.
Kinetic (Sliding) Friction – The force that opposes motion when a body slides over another.
Laws of Friction
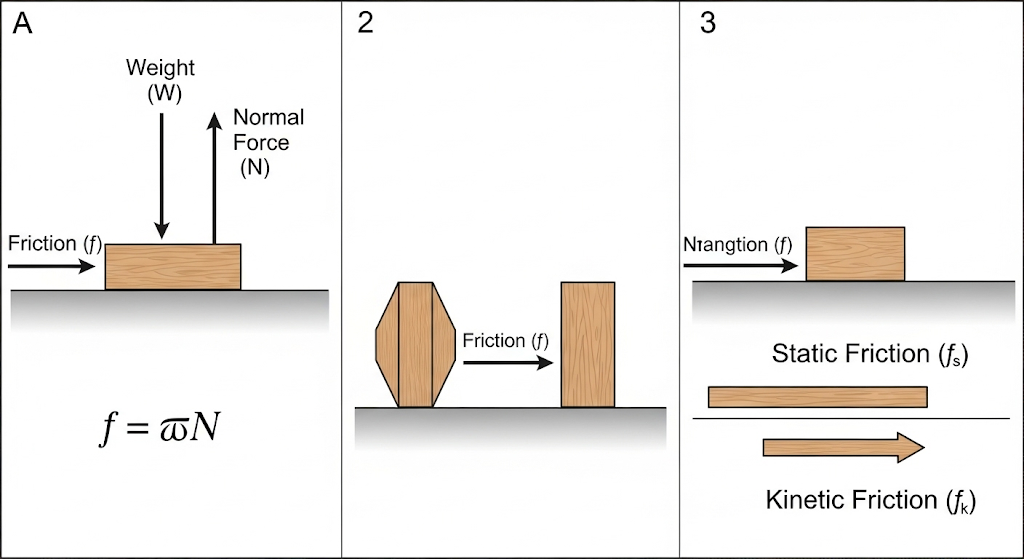
Friction is directly proportional to the normal reaction (f = μN).
Friction is independent of the area of contact.
Kinetic friction is usually less than maximum static friction.
| Advantages of Friction | Disadvantages of Friction |
|---|---|
| Helps us walk | Causes wear and tear of machines |
| Allows cars to move on roads | Wastes energy as heat |
| Enables writing with pen or pencil | Reduces efficiency |
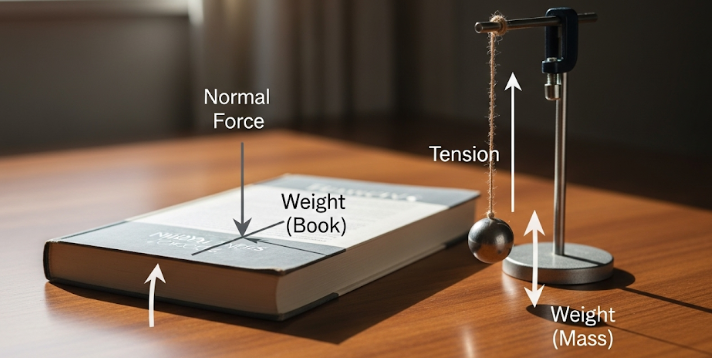
Equilibrium of a Particle
A particle is said to be in equilibrium when the vector sum of all forces acting on it is zero.
Conditions of Equilibrium
- ΣFx = 0 (sum of forces in horizontal direction = 0)
- ΣFy = 0 (sum of forces in vertical direction = 0)
Examples: A hanging mass at rest is in equilibrium when tension balances weight.
A book resting on a table is in equilibrium because the weight is balanced by the normal reaction.
Circular Motion
When a body moves along a circular path, it undergoes circular motion. The direction of velocity changes continuously, so there is always an acceleration directed toward the center of the circle. This is called centripetal acceleration.

Centripetal Force
The force required to keep a body in circular motion is given by:
Fc = mv² / r
Where,
m = mass of body, v = velocity, r = radius of circle
Solved Example – Circular Motion
Q: A car of mass 1000 kg moves around a curve of radius 50 m at 10 m/s. Find the centripetal force.
Solution:
Fc = mv² / r = 1000 × 100 / 50 = 2000 N
So, the centripetal force is 2000 newtons.
Key Points of Friction, Equilibrium, and Circular Motion
- Friction can be static, sliding, or rolling.
- Equilibrium occurs when net force is zero.
- Circular motion requires centripetal force toward the center.
- Banking of roads provides safety and stability for vehicles.
Banking of Roads
When a vehicle goes around a curved road, it needs centripetal force. Roads are banked (tilted) at an angle θ to provide the necessary force.

Condition for no friction:
tanθ = v² / (rg)
Advantages of Banking:
Risk of skidding is minimized.
Vehicles can turn safely at higher speeds.
Laws of motion high school physics -Examples from the Chapter
Example 4.1 Book at rest and car in uniform motion (illustrating Newton’s First Law).
Solution : A book lying on a table stays at rest because its weight downward is exactly balanced by the normal reaction upward. Net force = 0, so the book does not move.
A car moving with constant speed on a level road continues uniformly because the forward driving force of the engine balances the resistive forces of friction and air. Net force = 0, so velocity remains constant.
This illustrates Newton’s First Law: if net external force is zero, the state of motion does not change.
Example 4.2 A bullet entering a wooden block, finding average resistive force. laws of motion
Sol: Mass of bullet = 0.04 kg
Initial speed = 90 m/s
Final speed = 0
Stopping distance = 0.6 m
Using equation of motion:
v² = u² + 2as
0 = (90)² + 2 × a × 0.6
a = – 8100 / 1.2 = – 6750 m/s²
Force = m × a = 0.04 × 6750 = 270 N
Example 4.3 – Motion given by y = u t + 1/2 g t^2 (show F = m g)
Sol: Given motion: y = u t + 1/2 g t^2
- Velocity v = dy/dt = u + g t.
- Acceleration a = dv/dt = g (constant).
- By Newton’s second law, net force F = m × a = m × g.
Example 4.4 Motion of a body sliding down an inclined plane with friction. (Earlier section)laws of motion
Sol:
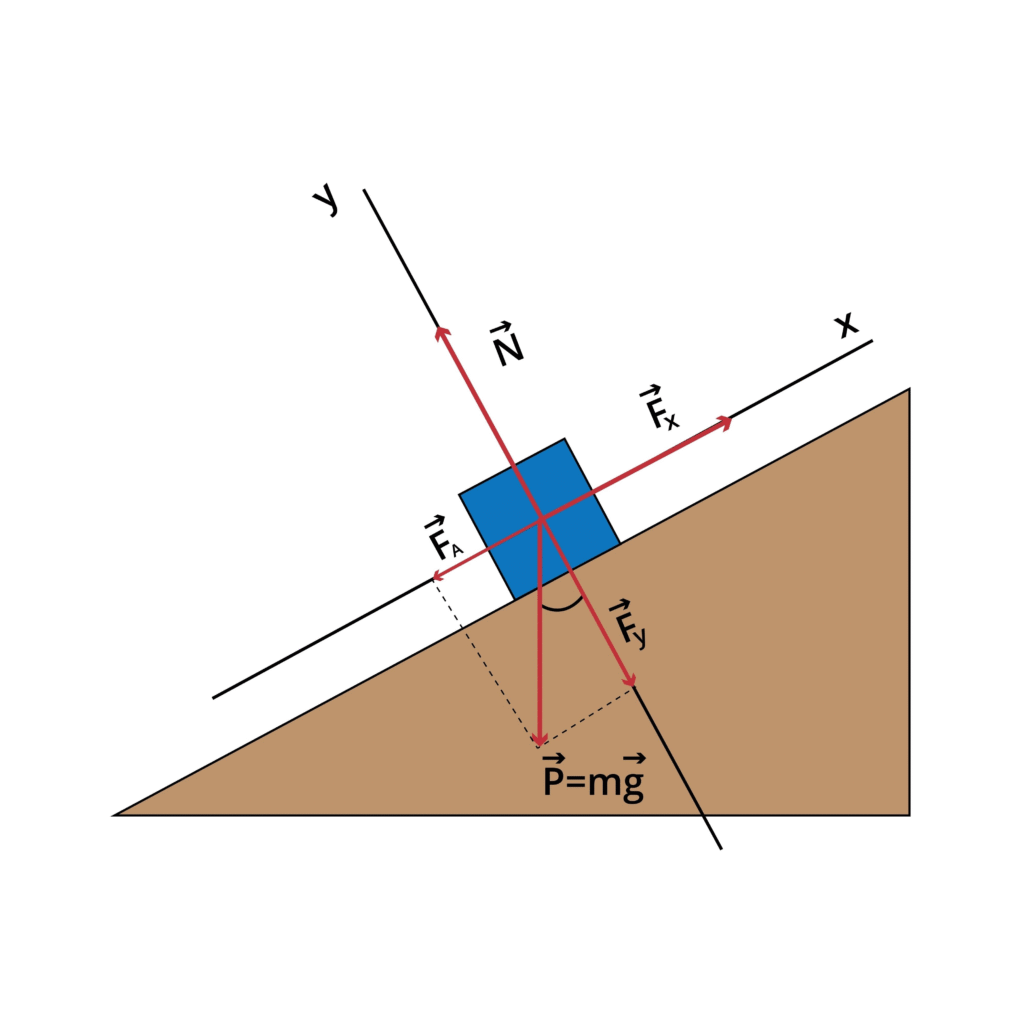
Consider a block of mass m placed on an inclined plane at angle θ. The surface has coefficient of friction μ.
Step 1: Resolve forces
Component of weight perpendicular to plane = m g cos θ.
Weight of block = m g (acts vertically downward).
Component of weight along the plane = m g sin θ (downwards).
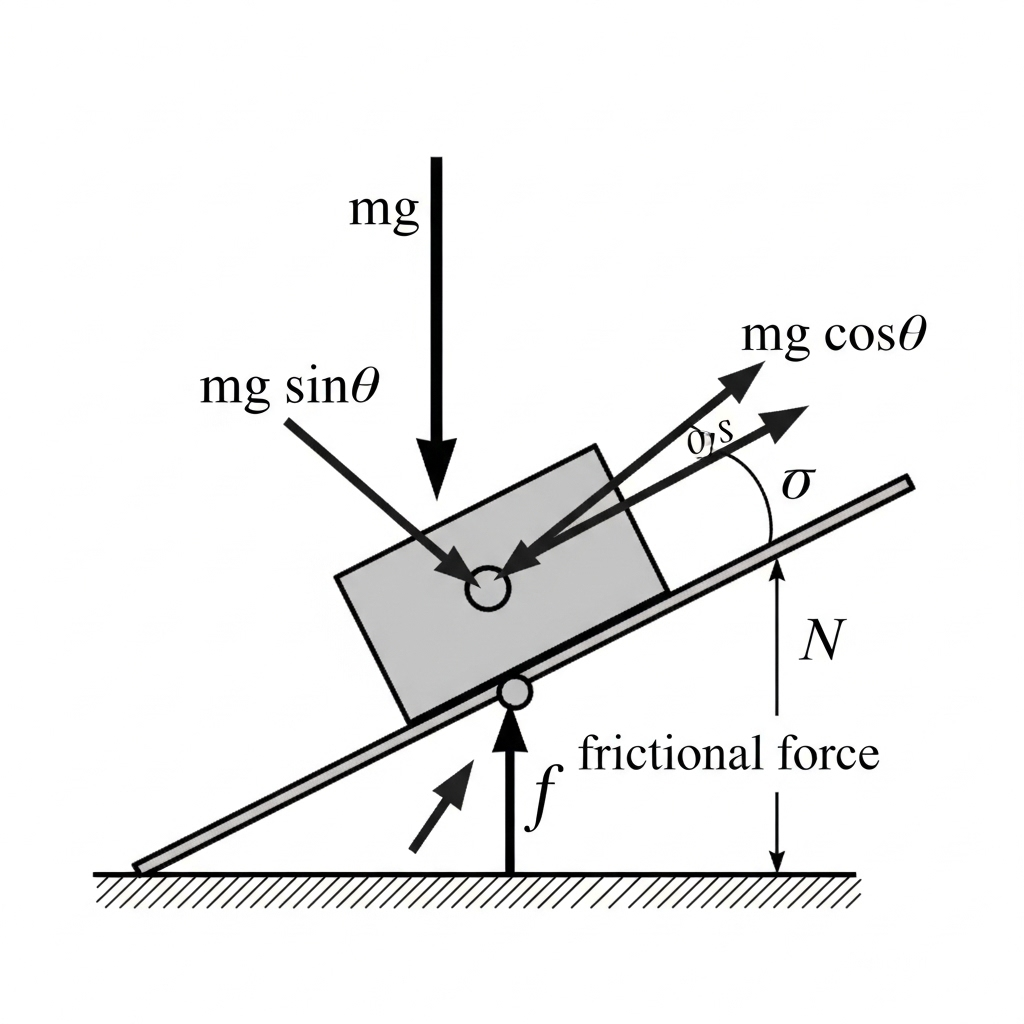
Step 2: Normal reaction
Normal reaction N = m g cos θ.
Step 3: Frictional force
Friction = μ × N = μ m g cos θ, acting up the plane (opposite motion).
Step 4: Net force along plane
Net force = m g sin θ – μ m g cos θ.
Step 5: Acceleration
Using F = m a,
a = (Net force) / m = g (sin θ – μ cos θ).
Example 4.5 Two billiard balls striking a rigid wall at different angles, impulse and direction of force.
Ans:
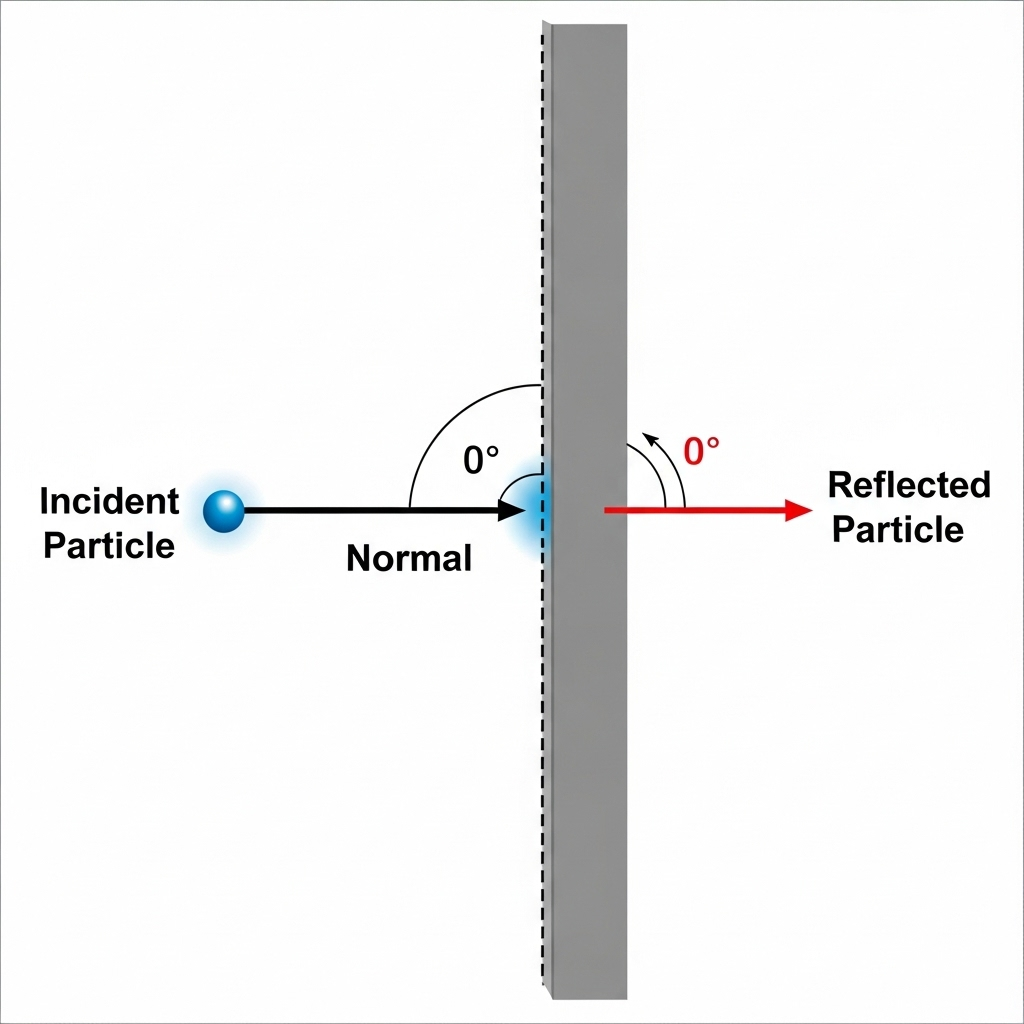
Case (a) – Normal incidence
- Initial momentum along normal = – m u (towards the wall).
- Final momentum along normal = + m u (away from the wall).
- Change in momentum = + m u – (– m u) = 2 m u.
- Impulse = 2 m u, directed normal to the wall.
- The force on the wall is opposite, directed into the wall.
Case (b) – Incidence at 30°
- Resolve velocity:
- Normal component = u cos 30.
- Tangential component = u sin 30.
- Initial normal momentum = – m u cos 30.
- Final normal momentum = + m u cos 30 (reversed).
- Change in normal momentum = 2 m u cos 30.
- Tangential momentum does not change (smooth wall, no friction).
- Impulse = 2 m u cos 30, normal to the wall.
Comparison of impulses
Impulse in case (a) : impulse in case (b) = (2 m u) : (2 m u cos 30) = 1 : cos 30.
Since cos 30 ≈ 0.866, the impulse in case (b) is smaller.
Example 4.6 A 6 kg mass suspended by rope with a 50 N horizontal force, equilibrium angle of rope.
Ans:
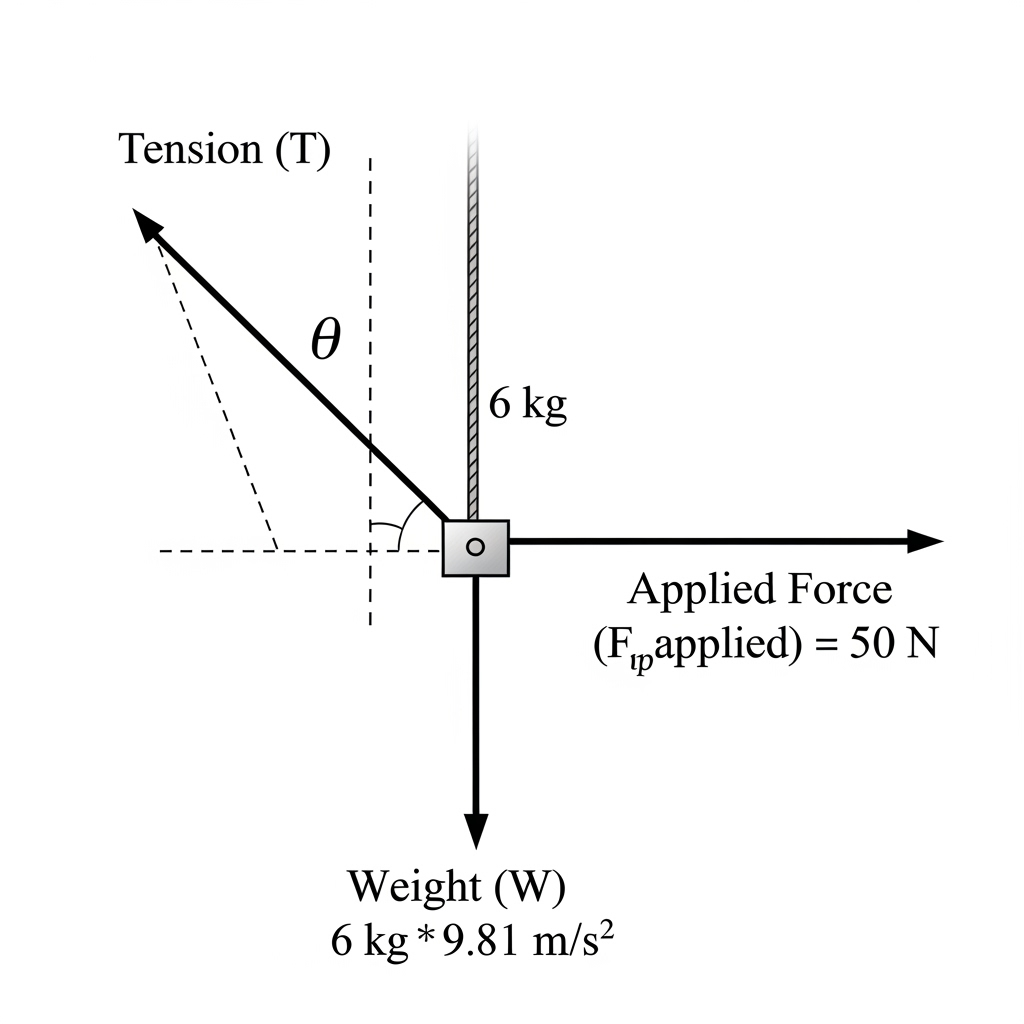
Given:
Mass of the block = 6 kg.
Acceleration due to gravity g = 10 m/s².
Therefore, weight of block W = 6 × 10 = 60 N (downward).
A horizontal force of 50 N is applied. The block is in equilibrium.
- Forces acting on the block are:
- Weight = 60 N vertically downward.
- Tension T in the rope, making angle θ with the vertical.
- Horizontal force = 50 N.
- Resolve tension into components:
- Vertical component: T cos θ (balances weight).
- Horizontal component: T sin θ (balances 50 N).
- Equilibrium conditions:
- Vertical: T cos θ = 60
- Horizontal: T sin θ = 50
- Divide horizontal by vertical:
tan θ = 50 / 60 = 5/6. - θ = arctan (5/6) ≈ 39.8°.
Example 4.7 A block and trolley system with friction, solved using Newton’s Second Law.
Ans:
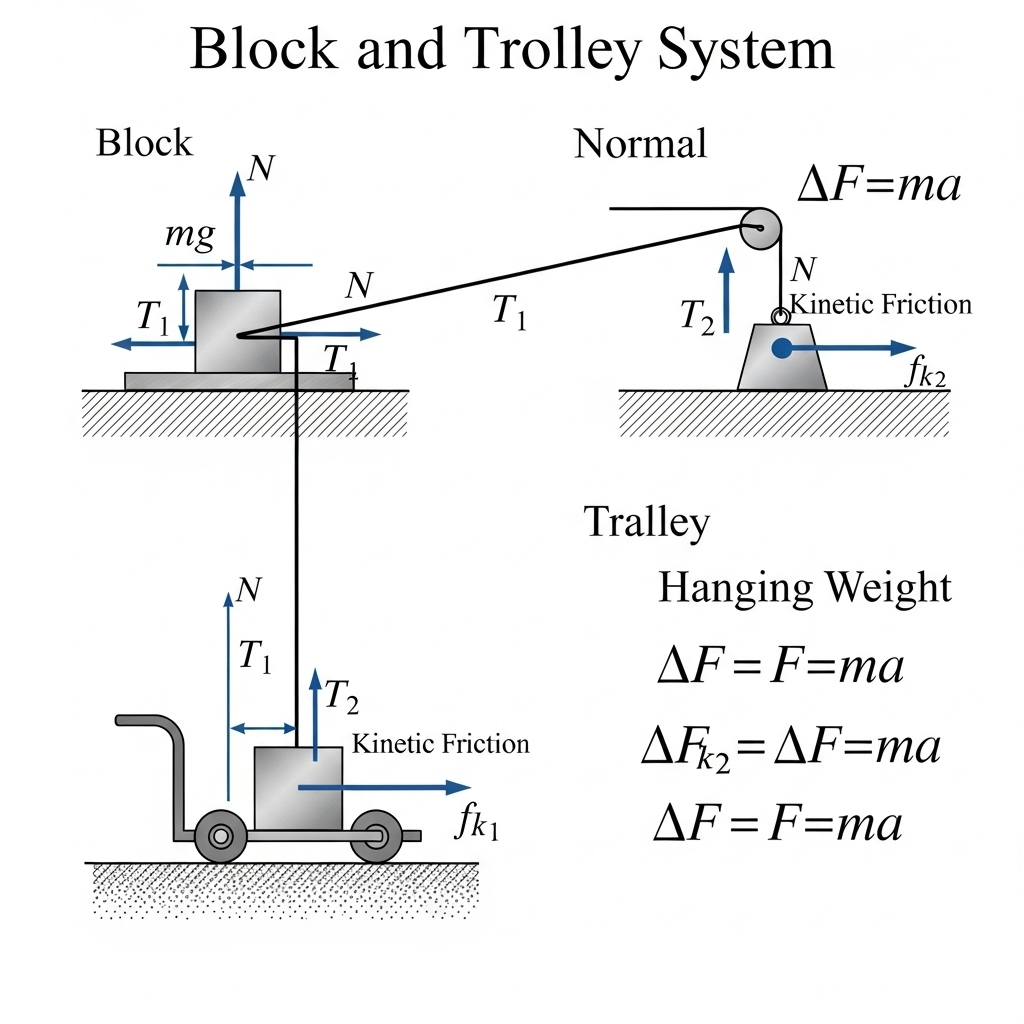

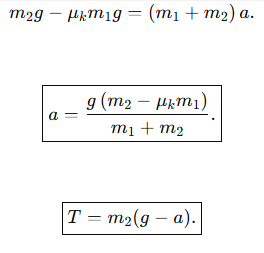

Example 4.8 Car moving on a level road, static friction providing centripetal force.
Ans:
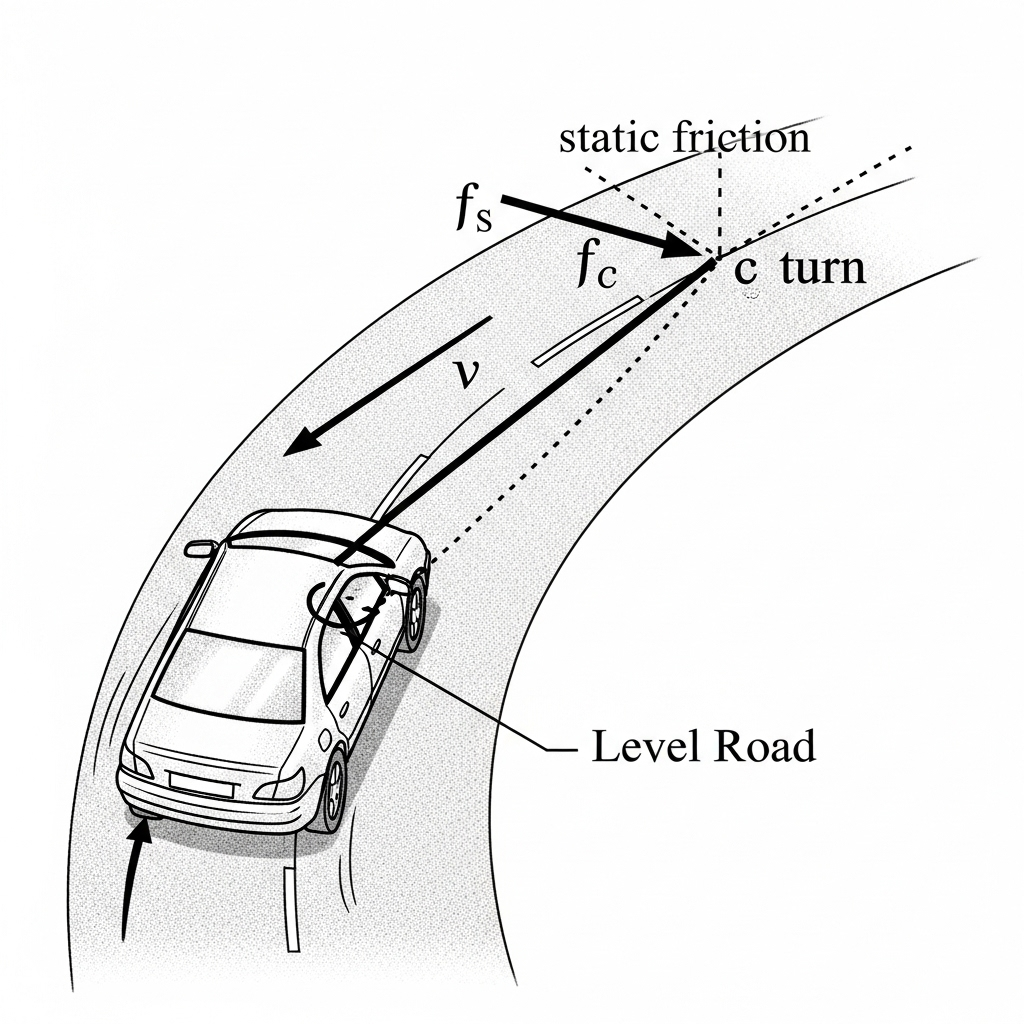


Example 4.9 Motion on a banked road without friction.
Ans:
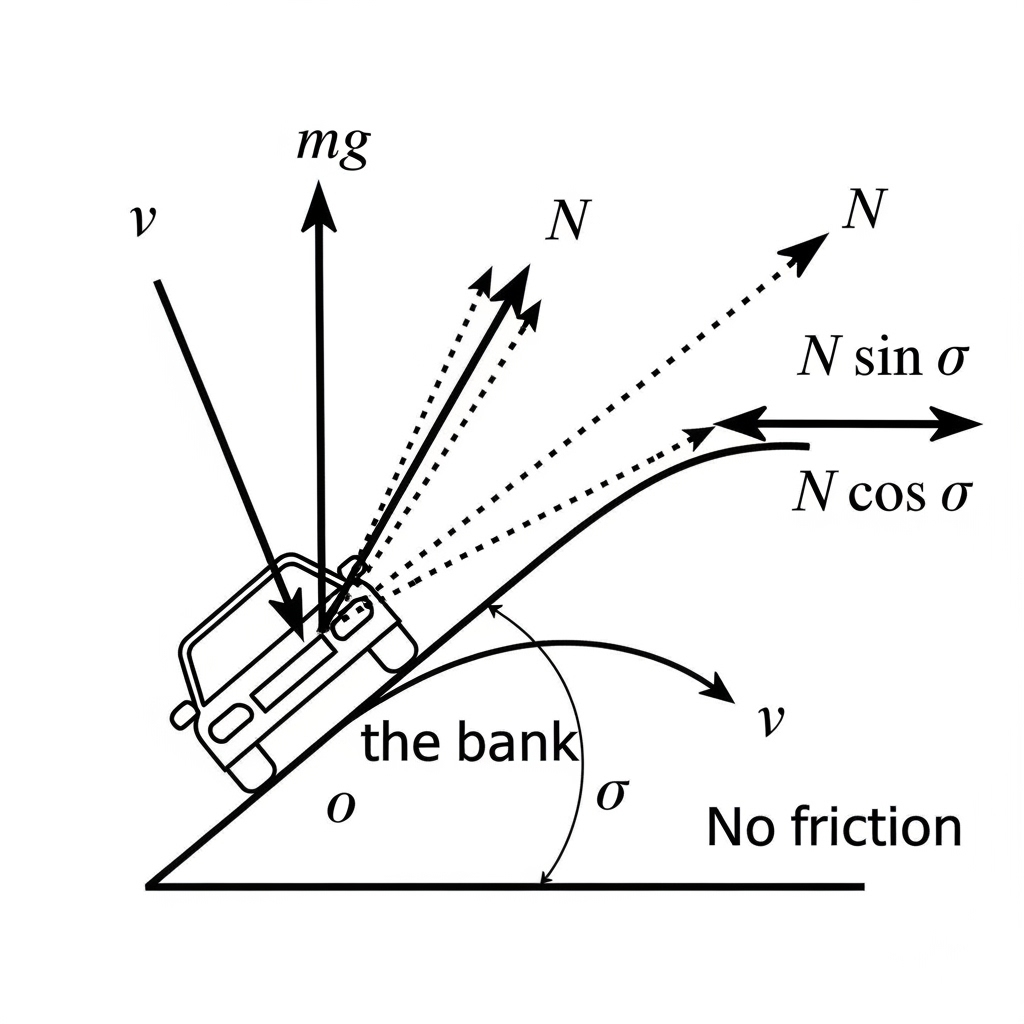


Example 4.10 Car on banked road with friction included. (extended formula)
Ans:
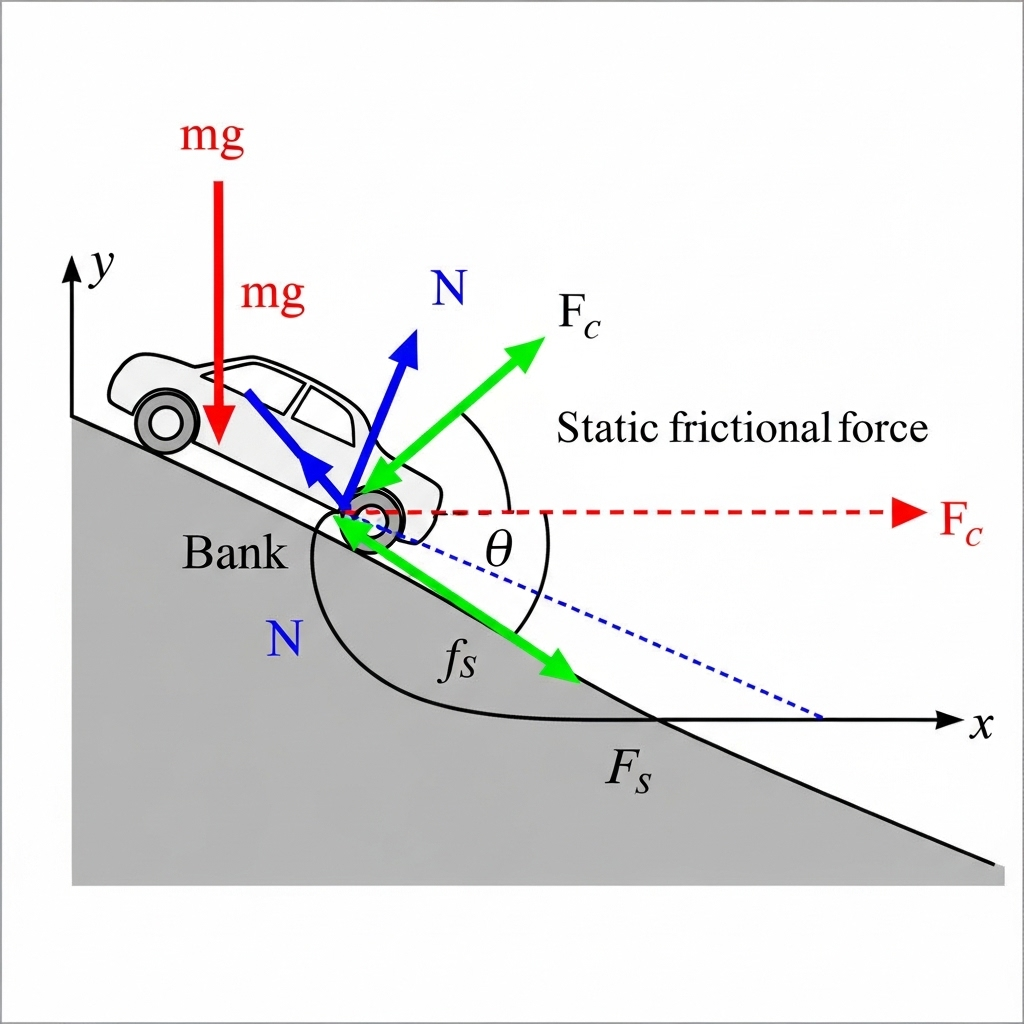



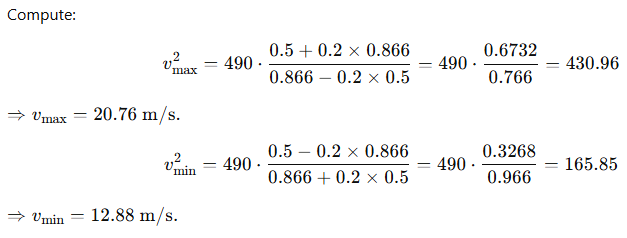
Example 4.11 Circular racetrack (banked at 15°), optimum speed and max speed of car.
Ans:
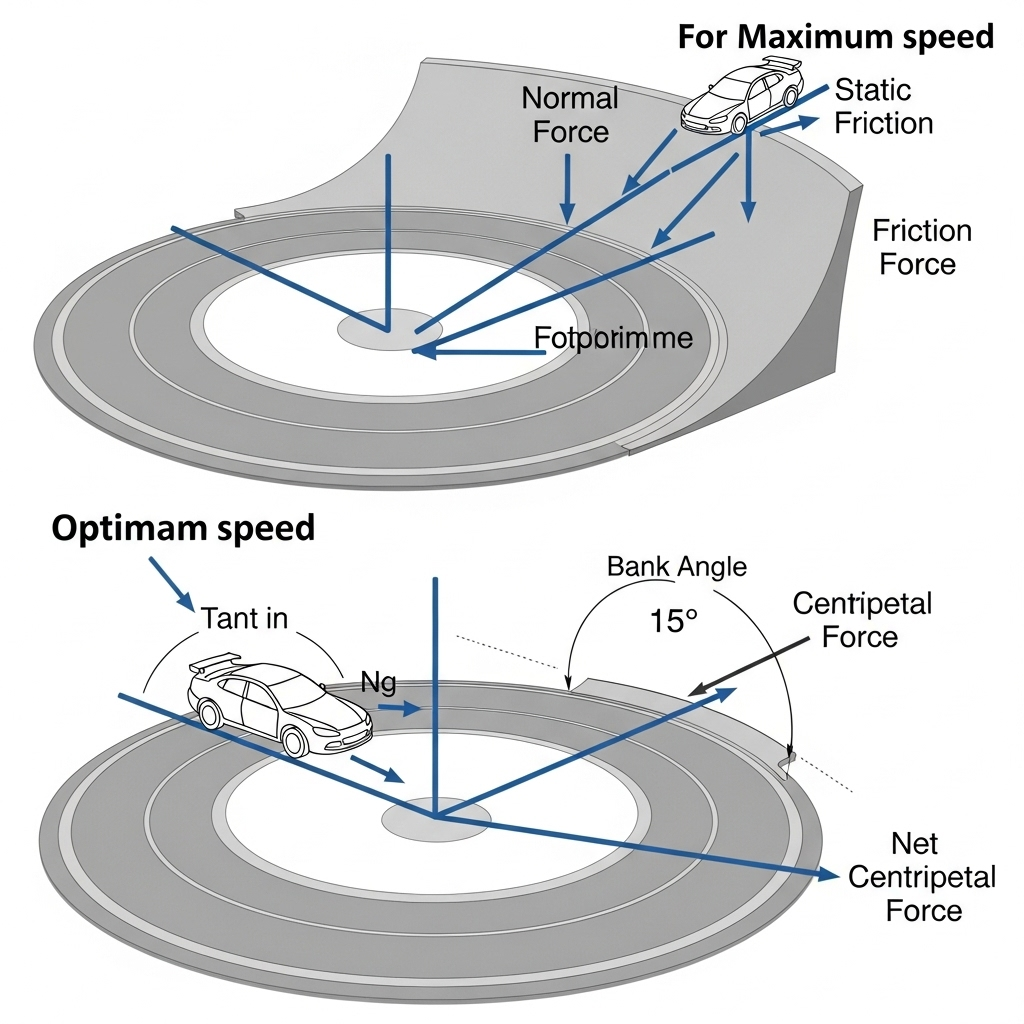
A banked curve is a road tilted toward the centre of the turn.
When a car goes around such a curve, the tyre pushes on the road and the road’s normal force has a horizontal part. That horizontal part helps turn the car, so the car does not need as much friction to stay on the track.
In this example we will find
- the optimum speed at which no friction is needed, and
- the maximum safe speed when static friction is available.
One-line idea: the horizontal component of the normal force provides the centripetal force needed for turning.

All Exercise Questions
4.1 Net force magnitude and direction for:
(a) drop of rain falling at constant speed,
(b) cork floating,
(c) stationary kite,
(d) car moving with constant velocity,
(e) high-speed electron in empty space.
Ans: (a) Drop of rain falling at constant speed — Net force = 0 N. (Weight downward balanced by air-resistance upward; no resultant direction.)
(b) Cork floating — Net force = 0 N. (Weight down = buoyant force up; no resultant direction.)
(c) Stationary kite — Net force = 0 N. (Tension + aerodynamic lift/drag + weight balance; no resultant direction.)
(d) Car moving with constant velocity — Net force = 0 N. (Driving force = resistive forces; no resultant direction.)
(e) High-speed electron in empty space — Net force = 0 N (if no external fields present).
(If electric/magnetic fields exist, then
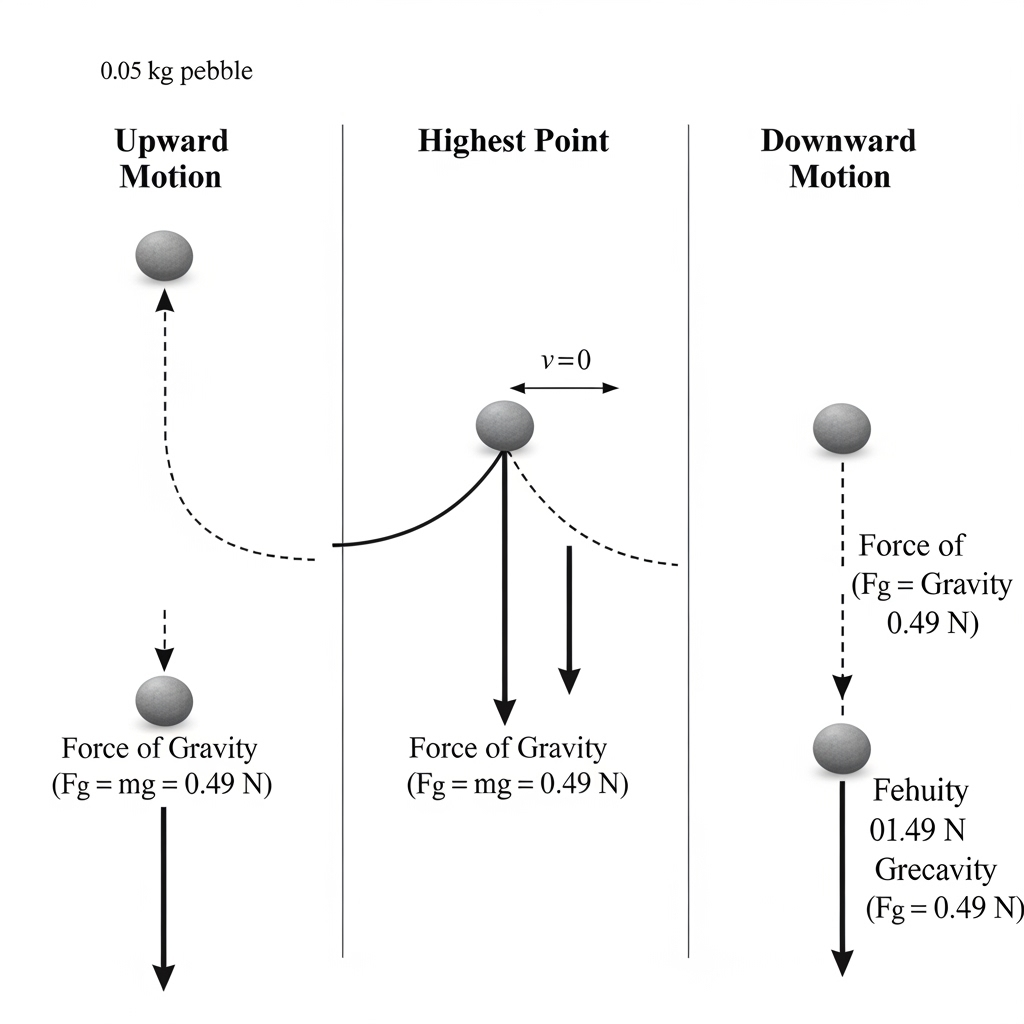
4.2 Pebble (0.05 kg) thrown vertically upwards: force during upward, downward, and at highest point.
Ans:

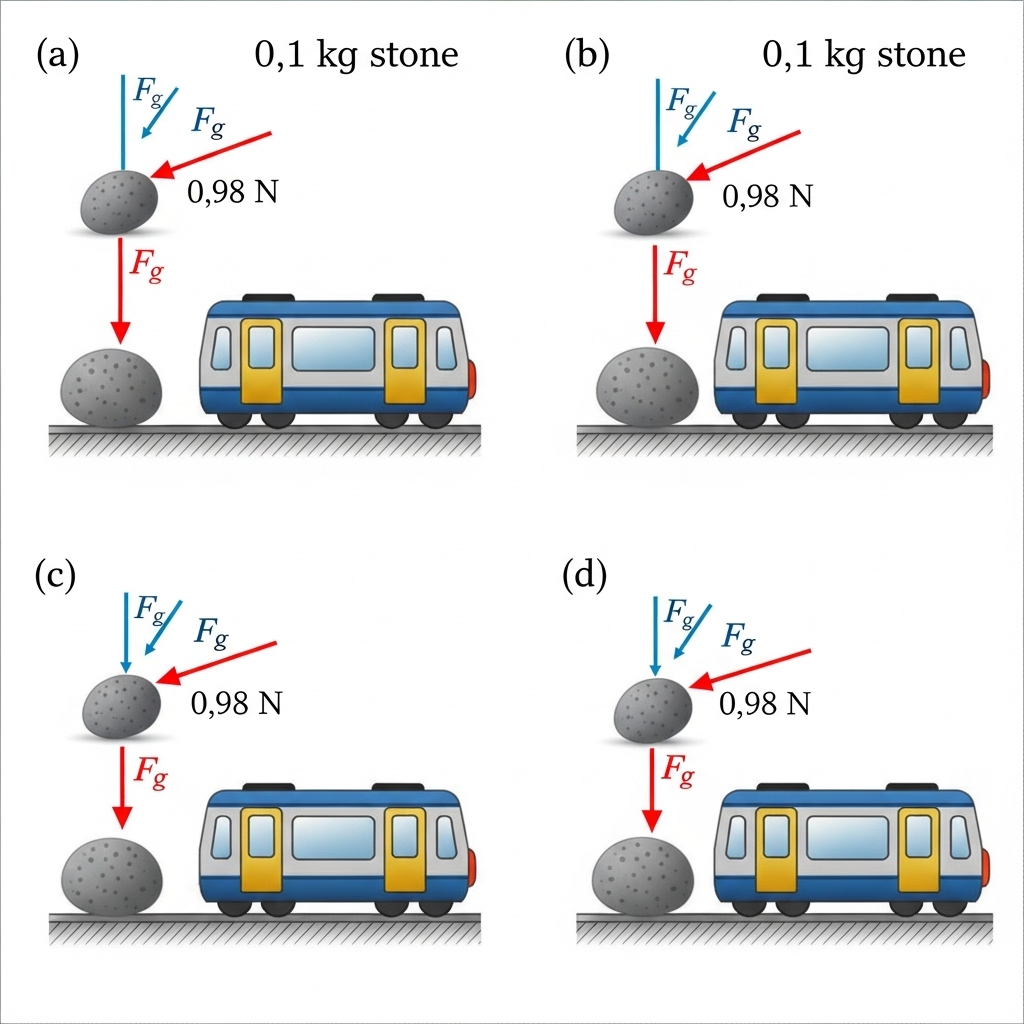
4.3 Net force on a stone (0.1 kg):
(a) dropped from stationary train,
(b) dropped from train at 36 km/h constant velocity,
(c) dropped from train accelerating at 1 m/s²,
(d) resting on floor of accelerating train.
Ans:


4.4 Particle of mass mmm tied with string length lll, moving in circle with speed vvv. Net force?

4.5 Retarding force of 50 N on 20 kg body moving with 15 m/s. Time to stop?
Ans:
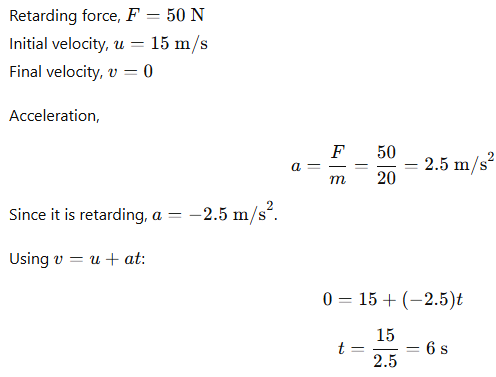
4.6 Constant force on 3.0 kg body changes speed from 2.0 to 3.5 m/s in 25 s. Find magnitude and direction of force.
Ans:
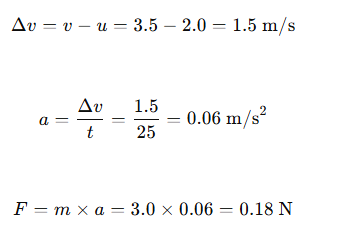
Direction: Since the velocity increases, the force acts along the direction of motion.
4.7 A 5 kg body acted by two perpendicular forces (8 N, 6 N). Find acceleration magnitude and direction.
Ans:

4.8 Three-wheeler (400 kg + driver 65 kg) moving at 36 km/h, stopped in 4.0 s. Find average retarding force.
Ans:
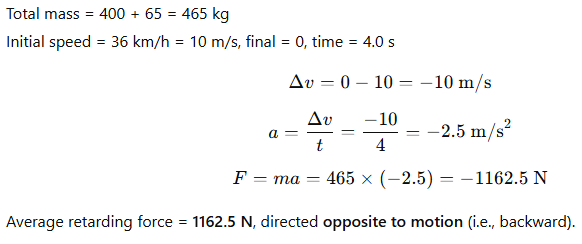
4.9 Rocket (20,000 kg) blasted upwards with initial acceleration 5 m/s². Find initial thrust.
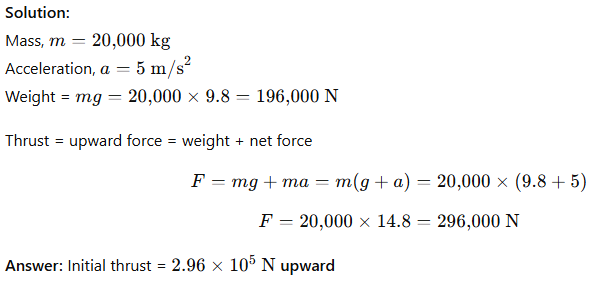
4.10 A 0.40 kg body moving north at 10 m/s, subject to 8 N south force for 30 s. Predict position at t = -5s, 25s, 100s.



4.11 Truck accelerates at 2 m/s². At t = 10s, stone dropped from top (6 m high). Find velocity and acceleration at t = 11s.

4.12 Pendulum bob (0.1 kg, string length 2 m, speed at mean = 1 m/s). Find trajectory if string is cut at (a) extreme position, (b) mean position.
Ans:

4.13 Man (70 kg) in lift with weighing scale:
(a) moving up at 10 m/s uniform speed,
(b) moving down with 5 m/s² acceleration,
(c) moving up with 5 m/s² acceleration,
(d) free fall.
Ans:


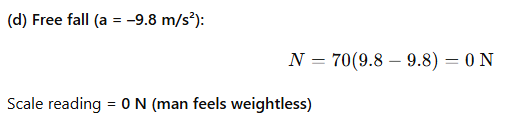
4.14 Position-time graph of particle (4 kg). Find force for different intervals and impulse at t = 0, 4s.
Ans:
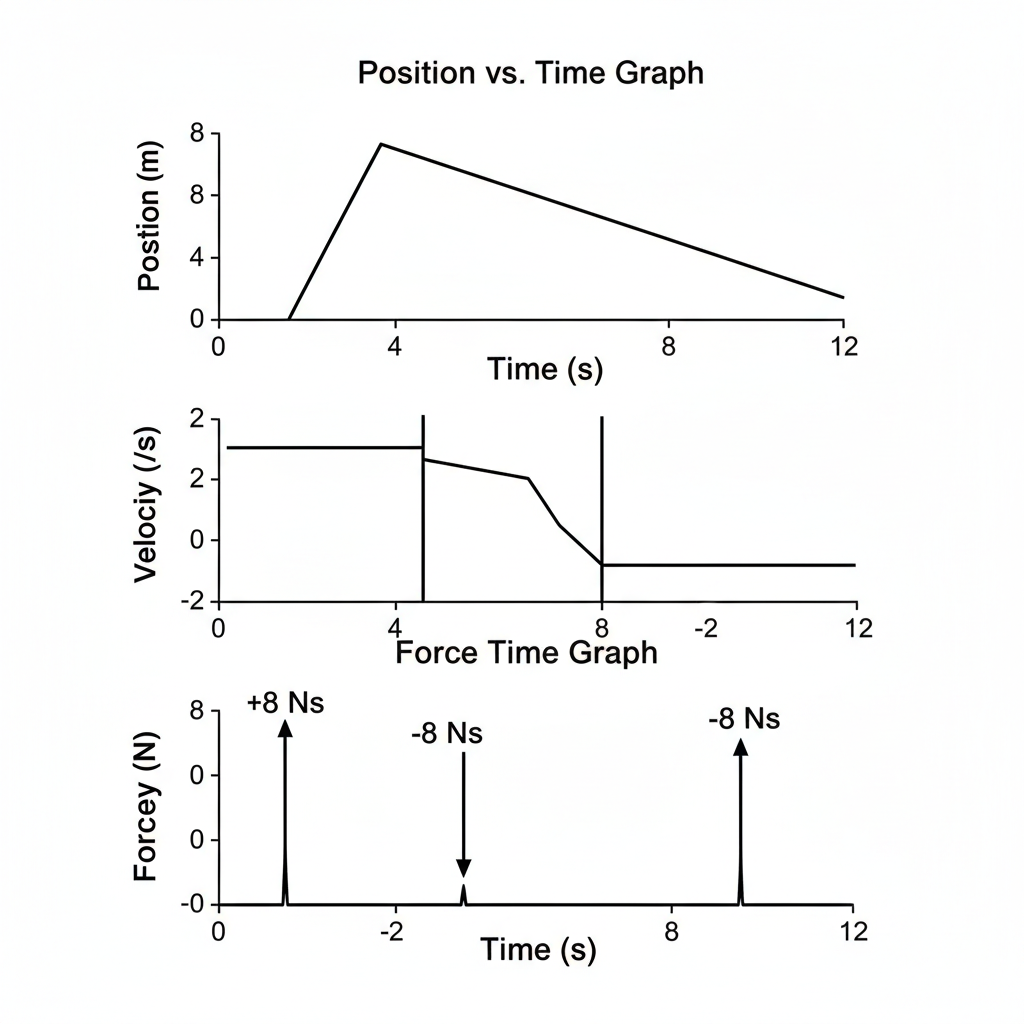
Imagine three aligned graphs, one below the other, sharing the same time axis.
From t = 8 s to t = 12 s: A horizontal line at F = 0 N.
Position-Time Graph (x vs. t):
Axes: Horizontal axis is Time (s), Vertical axis is Position (m).
Curve:
From t = 0 s to t = 4 s: A straight line starting from (0, 0) and going up to (4, 8). This represents constant positive velocity.
From t = 4 s to t = 8 s: A horizontal straight line from (4, 8) to (8, 8). This represents zero velocity (at rest).
From t = 8 s to t = 12 s: A straight line from (8, 8) down to (12, 0). This represents constant negative velocity.
Velocity-Time Graph (v vs. t): (Derived from the slopes of the position-time graph)
Axes: Horizontal axis is Time (s), Vertical axis is Velocity (m/s).
Curve: From t = 0 s to t = 4 s: A horizontal line at v = 2 m/s.
At t = 4 s: An instantaneous vertical drop from v = 2 m/s to v = 0 m/s (representing the sudden change in velocity/impulse).
From t = 4 s to t = 8 s: A horizontal line at v = 0 m/s.
At t = 8 s: An instantaneous vertical drop from v = 0 m/s to v = -2 m/s.
From t = 8 s to t = 12 s: A horizontal line at v = -2 m/s.
Force-Time Graph (F vs. t): (Derived from F = ma = m * dv/dt)
Axes: Horizontal axis is Time (s), Vertical axis is Force (N).
Curve:
From t = 0 s to t = 4 s: A horizontal line at F = 0 N.
At t = 0 s: A positive, infinitely thin spike (Dirac delta function) representing the impulse of 8 Ns. The “height” of this spike is infinite, but its area is 8 Ns.
At t = 4 s: A negative, infinitely thin spike representing the impulse of -8 Ns. Its area is -8 Ns.
From t = 4 s to t = 8 s: A horizontal line at F = 0 N.
At t = 8 s: A negative, infinitely thin spike representing the impulse of -8 Ns. Its area is -8 Ns.
4.15 Two bodies (10 kg, 20 kg) on smooth surface tied by string. Horizontal force 600 N applied on A or B. Find tension in string.
4.16 Masses 8 kg and 12 kg connected by pulley. Find acceleration and tension.
Ans:
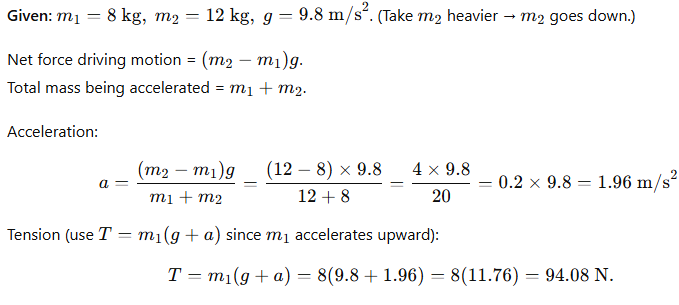
4.17 Nucleus at rest disintegrates into two smaller nuclei. Show products move in opposite directions.
Ans: Initial momentum = 0 (nucleus at rest). By conservation of linear momentum, total final momentum must also be 0. If the two product nuclei have masses m1 and m2 and velocities v1 and v2
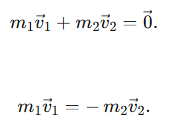

4.18 Two billiard balls (0.05 kg each, opposite direction, 6 m/s) collide and rebound with same speed. Find impulse on each ball.
Ans:


4.19 Shell (0.020 kg) fired from gun (100 kg) with muzzle speed 80 m/s. Find recoil speed of gun.

4.20 Batsman deflects ball (0.15 kg, 54 km/h) by 45° without changing speed. Find impulse imparted.
4.21 Stone (0.25 kg) tied to string radius 1.5 m, speed 40 rev/min. Find tension. Also find max speed if string can withstand 200 N.
4.22 If speed in Q4.21 exceeds limit and string breaks, describe trajectory:
(a) radial outward, (b) tangential, (c) at angle depending on speed.
4.23 Explain:
(a) horse cannot pull cart in empty space,
(b) passengers thrown forward when bus stops,
(c) easier to pull than push lawn mower,
(d) cricketer moves hands back while catching.
Ans: (a) Horse cannot pull cart in empty space
In empty space there is no external resistance (like ground friction) for the horse’s feet to push against. The horse pushes backward on the ground, and the ground reacts forward on the horse (Newton’s 3rd law). Without ground (in space), no reaction force → horse and cart cannot move forward.
(b) Passengers thrown forward when bus stops suddenly
When the bus stops, the lower part of passengers’ bodies is brought to rest by contact with the seat/floor, but their upper bodies tend to continue moving forward due to inertia of motion. Hence, they are thrown forward.
(c) Easier to pull than push a lawn mower
When you pull, the applied force makes an upward component that reduces the effective weight, decreasing friction. When you push, the applied force has a downward component that increases effective weight and friction. Thus, pulling requires less force than pushing.
(d) Cricketer moves hands backward while catching a ball
The ball has large momentum. By moving the hands back, the time of contact increases, so the rate of change of momentum (force) decreases. Smaller force reduces pain and prevents injury.
NEET Biology MCQs – Solved Previous Year Questions
NCERT Resource Hub
Math & Science Solutions by Class
- Class 10 Math Solutions
- Class 10 Science Solutions
- Class 9 Math Solutions
- Class 9 Science Solutions
- Class 8 Math Solutions
- Class 8 Science Solutions
