Areas Related To Circle Class 10 Ex 12.1- Solution For Math

Get clear and detailed Areas Related to Circle Class 10–Ex 12.1 with step-by-step answers to help you prepare effectively for your exams.

These solutions follow the latest NCERT guidelines and are ideal for revision, practice, and building a strong foundation in Class 10 Maths Chapter 12.

Table of contents

Class10 Math NCERT Solutions

Question 1.
The radii of the two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has a circumference equal to the sum of the circumferences of the two circles.

Solution:
Given:

Radius of the first circle = 19 cm
Radius of the second circle = 9 cm

We are to find the radius of a new circle whose circumference is equal to the sum of the circumferences of the two given circles.

Step 1: Use the formula for circumference of a circle

Circumference = 2 × π × radius

Circumference of the first circle = 2 × π × 19 = 38π cm
Circumference of the second circle = 2 × π × 9 = 18π cm

Step 2: Add both circumferences

Total circumference = 38π + 18π = 56π cm

Step 3: Let the radius of the new circle be R

Since 2 × π × R = 56π
Divide both sides by 2π:

R = 56π ÷ 2π = 28 cm

Question 2.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.

Solution:
Given:

Radius of the first circle = 8 cm
Radius of the second circle = 6 cm

We are to find the radius (R) of a new circle whose area is equal to the sum of the areas of the two given circles.

Step 1: Use the formula for the area of a circle

Area = π × radius²

Area of the first circle = π × 8² = π × 64
Area of the second circle = π × 6² = π × 36

Step 2: Add both areas

Total area = π × 64 + π × 36 = π × (64 + 36) = π × 100

Step 3: Let the radius of the new circle be R

Area of the new circle = π × R²
So, π × R² = π × 100
Cancel π from both sides:

R² = 100
R = √100 = 10 cm

Question 3.
The given figure depicts an archery target marked with its five scoring regions from the center outwards as Gold, Red, Blue, Black, and White.
The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Solution:
Given:

The target has 5 concentric circular scoring regions:
Gold (center), then Red, Blue, Black, and White (outermost).
Diameter of the Gold region = 21 cm, so its radius = 21 ÷ 2 = 10.5 cm
Each of the other bands (Red, Blue, Black, White) is 10.5 cm wide

We’ll calculate the area of each circular ring (annular region) using the formula:

Area of a circular ring = π × (R² – r²)
Where:

R = outer radius
r = inner radius

Step-by-step Calculation (all radii in cm, π = 3.1416 (approx.):

Gold region:

Inner radius = 0
Outer radius = 10.5
Area = π × (10.5² – 0²) = 3.1416 × 110.25 ≈ 346.36 cm²

Red region:

Inner radius = 10.5
Outer radius = 10.5 + 10.5 = 21
Area = π × (21² – 10.5²) = 3.1416 × (441 – 110.25) = 3.1416 × 330.75 ≈ 1038.10 cm²

Blue region:

Inner radius = 21
Outer radius = 21 + 10.5 = 31.5
Area = π × (31.5² – 21²) = 3.1416 × (992.25 – 441) = 3.1416 × 551.25 ≈ 1732.57 cm²

Black region:

Inner radius = 31.5
Outer radius = 31.5 + 10.5 = 42
Area = π × (42² – 31.5²) = 3.1416 × (1764 – 992.25) = 3.1416 × 771.75 ≈ 2423.68 cm²

White region:

Inner radius = 42
Outer radius = 42 + 10.5 = 52.5
Area = π × (52.5² – 42²) = 3.1416 × (2756.25 – 1764) = 3.1416 × 992.25 ≈ 3117.72 cm²

Final Answers (Approximate Areas):

Region	Area (cm²)
Gold	346.36
Red	1038.10
Blue	1732.57
Black	2423.68
White	3117.72

Question 4.
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?

Solution:
The diameter of each wheel is 80 cm, so the radius is 40 cm.

The speed of the car is 66 km/h.
Convert this to centimeters per hour:
66 × 100,000 = 6,600,000 cm/h.

Convert this to centimeters per minute:
6,600,000 ÷ 60 = 110,000 cm/min.

In 10 minutes, the car travels:
110,000 × 10 = 1,100,000 cm.

The circumference of one wheel is:
2 × π × 40 ≈ 2 × 3.1416 × 40 = 251.33 cm.

Number of revolutions = total distance ÷ circumference
= 1,100,000 ÷ 251.33 ≈ 4375.45.

Since only complete revolutions count, the number of complete revolutions is 4375.

Final answer: Each wheel makes 4375 complete revolutions in 10 minutes.

Question 5.
Tick the correct answer in the following and justify your choice: If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(a) 2 units
(b) n units
(c) 4 units
(d) 7 units
Solution:
Let the radius of the circle be r units.
Perimeter (circumference) = 2πr
Area = πr²

Given:
2πr = πr²

Divide both sides by π:
2r = r²

Divide both sides by r (assuming r ≠ 0):
2 = r

Therefore, the radius of the circle is 2 units.

Correct answer: (a) 2 units

Terms Related To Circle

(i) Chord: A line segment joining any two points on a circle.
(ii) Arc: A piece of a circle between two points on the circle is called an arc.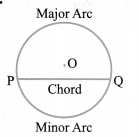
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.1 Mind Map 1
The arc less than the semicircular arc is called minor arc and the one greater than the semi-circular arc is called major arc.
(iii) Sector: The portion of a circular region enclosed by two radii and the corresponding arc is called a sector of the circle.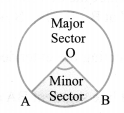
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.1 Mind Map 2
Sector smaller than the semi-circle is called minor sector and the sector larger than the semi-circle is called major sector.
(iv) Segment: The portion of a circular region enclosed between a chord and the corresponding arc is called a segment of the circle.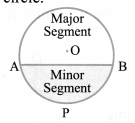
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.1 Mind Map 3
The segment bounded by the chord and the minor arc intercepted by the chord is called minor segment and the segment bounded by the chord and the major arc intercepted by the chord is called major segment.

Circle

The set of all points in a plane which are at a fixed distance from a fixed point in the plane is called circle. The fixed point is called centre and the fixed distance is called radius of the circle

Circumference and Area of a Circle
(i) The circumference of a circle is defined as distance covered by travelling once around a circle and is given by C = 2πr = πd
where r = radius of the circle and d = diameter of the circle.
(ii) The Area of a circle of radius r is given by,
A = πr2=π4d2 where, d = diameter of the circle.
(iii) Area of a circular ring:
The area of the circular path or ring is given by the difference of the area of outer circle and the area of inner circle.
Area of circular ring = n(R² – r²)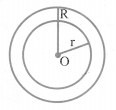
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.1 Mind Map 4

Length of an Arc and Area of Sector

(i) The length of an arc of a sector of an angle 9 is given by,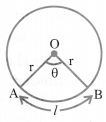
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.1 Mind Map 5
(ii) The area of the sector AOB of angle 0 is given by,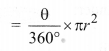

This is the area of minor sector.
∴ area of major sector AOB
= πr² – Area of a minor sector AOB

Area of Segment

(i) Area of segment APB = Area (sector OAPB) – Area(∆OAB)
This is the area of minor segment.
∴ area of major segment AQB = πr² – Area of minor segment APB

(ii) If θ is the central angle, then the area of segment APB

EX 12.2

📘 Math & Science Solutions by Class

🔹 Class 10

🔹 Class 9

🔹 Class 8

🔹 Class 7

🔹 Class 6

🔹 Class 11

Learn more about circle formulas from NCERT.

Class-wise Solutions

Class 12:

Class 12 Physics – NCERT Solutions

Class 12 Chemistry – NCERT Solutions

Class 11:

Class 10:

Class 9:

Class 8:

Class 7:

Class 7 Science – Oxford Solutions

Class 6:

Class 6 Science – Oxford Solutions

Subject-wise Solutions

Physics:

Chemistry:

Biology:

Class 11 Biology – NCERT Solutions

Math:

Science: