Welcome to Class 10 Math Ch 8 Trigonometry Ex 8.2. In this exercise, you will learn how to calculate trigonometric ratios for angles of elevation and depression, and solve related problems using right-angled triangles. Exercise 8.2 builds on the basics of trigonometric ratios introduced earlier and helps you apply these concepts to practical situations.

These step-by-step solutions are designed to help you understand how to find the values of sine, cosine, and tangent for different angles and use them to solve real-world problems confidently. Whether you are preparing for your exams or strengthening your concepts, this exercise is a great way to master trigonometry.
Class 10 Math Ch 8 Trigonometry Ex 8.2-Text Book Solutions
Ex 8.2 Class 10 Maths Question 1.
Evaluate the following:
Evaluate:
- (i) sin 60° cos 30° + sin 30° cos 60°
- (ii) 2 tan² 45° + cos² 30° − sin² 60°
- (iii) (cos 45° / sec 30° + cosec 30°)
- (iv) (sin 30° + tan 45° − cosec 60°) / (sec 30° + cos 60° + cot 45°)
- (v) (5 cos² 60° + 4 sec² 30° − tan² 45°) / (sin² 30° + cos² 30°)
Solution:
(i) sin 60° cos 30° + sin 30° cos 60°
We know:
sin 60° = √3/2, cos 30° = √3/2, sin 30° = 1/2, cos 60° = 1/2
sin 60° cos 30° = (√3/2)(√3/2) = 3/4
sin 30° cos 60° = (1/2)(1/2) = 1/4
Sum = 3/4 + 1/4 = 1
(ii) 2 tan² 45° + cos² 30° − sin² 60°
tan 45° = 1 → tan² 45° = 1² = 1
cos 30° = √3/2 → cos² 30° = 3/4
sin 60° = √3/2 → sin² 60° = 3/4
2 tan² 45° + cos² 30° − sin² 60° = 2(1) + 3/4 − 3/4 = 2
(iii) cos 45° / (sec 30° + cosec 30°)
cos 45° = √2/2
sec 30° = 1/cos 30° = 2/√3
cosec 30° = 1/sin 30° = 2/1 = 2
Denominator = sec 30° + cosec 30° = 2/√3 + 2 = 2(1/√3 + 1) = 2( (1 + √3)/√3 ) = 2(1 + √3)/√3
So fraction = (√2/2) ÷ (2(1 + √3)/√3) = (√2/2) × (√3 / 2(1 + √3)) = (√6) / (4(1 + √3))
(iv) (sin 30° + tan 45° − cosec 60°) / (sec 30° + cos 60° + cot 45°)
sin 30° = 1/2
tan 45° = 1
cosec 60° = 2/√3
Numerator = 1/2 + 1 − 2/√3 = 3/2 − 2/√3 = (3√3 − 4)/2√3
Denominator:
sec 30° = 2/√3, cos 60° = 1/2, cot 45° = 1
Denominator = 2/√3 + 1/2 + 1 = 2/√3 + 3/2 = (4 + 3√3)/2√3
So fraction = Numerator / Denominator = [(3√3 − 4)/2√3] ÷ [(4 + 3√3)/2√3] = (3√3 − 4)/(4 + 3√3)
(v) (5 cos² 60° + 4 sec² 30° − tan² 45°) / (sin² 30° + cos² 30°)
cos 60° = 1/2 → cos² 60° = 1/4 → 5 cos² 60° = 5 × 1/4 = 5/4
sec 30° = 2/√3 → sec² 30° = 4/3 → 4 sec² 30° = 16/3
tan 45° = 1 → tan² 45° = 1
Numerator = 5/4 + 16/3 − 1 = (15/12 + 64/12 − 12/12) = 67/12
Denominator: sin² 30° + cos² 30° = (1/2)² + (√3/2)² = 1/4 + 3/4 = 1
Area = Numerator / Denominator = 67/12
Ex 8.2 Class 10 Maths Question 2.
Choose the correct option and justify your choice: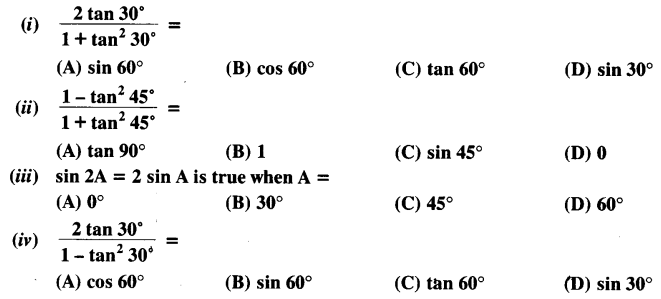
Solution:
Ex 8.2 Class 10 Maths Question 3.
If tan (A + B) = √3 and tan (A – B) = 1√3; 0° < A + B ≤ 90°; A > B, find A and B.
Solution: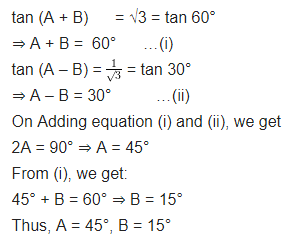
Ex 8.2 Class 10 Maths Question 4.
State whether the following statements are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution: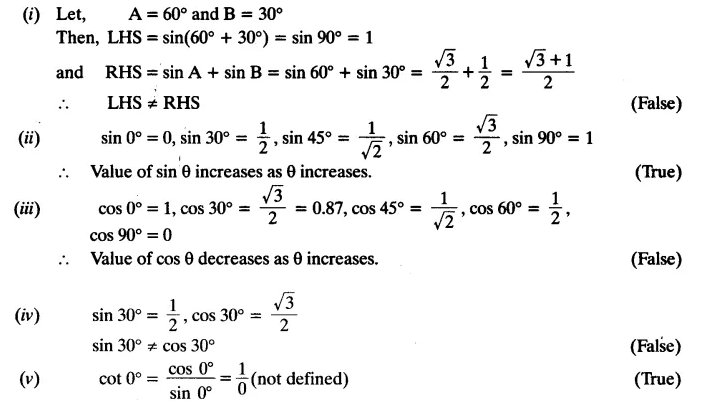
New Syllabus-
Question 1:
Express the trigonometric ratios sin A, sec A, and tan A in terms of cot A.
Solution:
Using the cotangent identity:
- sin A = 1 / √(1 + cot² A)
- sec A = √(1 + cot² A)
- tan A = 1 / cot A
Question 2:
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
We know the following identity:
- sec² A = 1 + tan² A
So:
- sin A = √(sec² A – 1) / sec A
- cos A = 1 / sec A
- tan A = √(sec² A – 1)
- cot A = 1 / √(sec² A – 1)
Question 3:
Choose the correct option. Justify your choice:
(i) 9 sec² A – 9 tan² A =
Options:
- (A) 1
- (B) 9
- (C) 8
- (D) 0
Solution:
We can simplify the expression:
9 sec² A – 9 tan² A = 9(sec² A – tan² A)
We know that:
sec² A – tan² A = 1
Thus:
9 sec² A – 9 tan² A = 9 × 1 = 9
Correct answer: (B) 9
(ii) (1 + tan θ + sec θ)(1 + cot θ – cosec θ) = ?
Solution:
This is an expression that requires substituting the values of tan θ, sec θ, cot θ, and cosec θ into their trigonometric identities to simplify further. It needs more information or values to be solved explicitly.
Question 4:
If sec A = 2, find:
(i) sin A
Solution:
We know that:
sec A = 1 / cos A
So:
cos A = 1 / sec A = 1 / 2
Using sin² A + cos² A = 1:
sin² A = 1 – (1 / 2)² = 1 – 1/4 = 3/4
sin A = √3 / 2
(ii) cos A
We already know that:
cos A = 1 / 2
(iii) tan A
Using:
tan A = sin A / cos A = (√3 / 2) / (1 / 2) = √3
(iv) cot A
Using:
cot A = 1 / tan A = 1 / √3
Question 5:
In triangle ABC, right-angled at B, if tan A = 1/3, find the value of:
(i) sin A cos C + cos A sin C
Solution:
Since triangle ABC is right-angled at B, angles A and C are complementary:
sin A cos C + cos A sin C = sin (A + C) = sin 90° = 1
(ii) cos A cos C – sin A sin C
Using the identity:
cos (A + C) = cos 90° = 0
Thus:
cos A cos C – sin A sin C = 0
Question 6:
In Δ PQR, right-angled at Q, if PR + QR = 25 cm and PQ = 5 cm. Determine the values of:
(i) sin P, cos P, and tan P
Solution:
Using the Pythagorean theorem:
PR² = PQ² + QR² = 5² + (25 – 5)² = 25 + 400 = 425
PR = √425
Now, calculate the trigonometric ratios:
sin P = PQ / PR = 5 / √425
cos P = QR / PR = 20 / √425
tan P = PQ / QR = 5 / 20 = 1 / 4
Question 7:
State whether the following are true or false. Justify your answer:
(i) The value of tan A is always less than 1.
Solution:
This is false. The value of tan A can be greater than 1 depending on the value of angle A. For example, tan 45° = 1, and tan 60° = √3 > 1.
(ii) sec A = 12.
Solution:
This is false because sec A = 12 is only valid for specific values of angle A. Without more context, we cannot assert that this is always true.
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
Class 10 Math Ch 8 Trigonometry Ex 8.2 is an important step towards understanding how trigonometric ratios can be applied to solve real-world problems involving right-angled triangles. In this exercise, you have practiced finding the values of sine, cosine, and tangent for various angles and applied these ratios to calculate unknown sides and angles in right triangles.
The problems in this exercise help build a strong foundation in the concept of trigonometric ratios by reinforcing how these ratios relate the angles to the sides of a triangle. This is essential not only for your current syllabus but also for future studies in mathematics, physics, and engineering. By mastering these concepts, you will be able to solve a variety of practical problems such as finding heights of buildings, lengths of objects, and distances that cannot be measured directly.
The step-by-step solutions provided here are aimed at simplifying each problem, ensuring that you understand the underlying logic and methods used to reach the answers. This approach is particularly helpful for students who want to strengthen their problem-solving skills and gain confidence in trigonometry.
Remember, consistent practice is key. As you work through more exercises and problems, your familiarity with trigonometric ratios and their applications will improve significantly. It is also important to review the basic definitions and identities of trigonometry regularly to maintain conceptual clarity.
In conclusion, Class 10 Math Ch 8 Trigonometry Ex 8.2 is a vital part of your trigonometry learning journey, providing you with the skills needed to apply mathematical concepts to real-life scenarios. Keep practicing these exercises to build a strong mathematical foundation and perform well in your exams.
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
