NCERT Solutions for Class 11 Physics Waves (Free PDF)

NCERT Solutions for Class 11 Physics Waves are designed to help students clearly understand the important concepts of the Waves chapter from the NCERT textbook. This chapter explains key topics such as types of waves, wave motion, speed of waves, superposition principle, sound waves, Doppler effect, and more.

These solutions provide step-by-step explanations in simple language, making it easier for students to prepare for school exams and competitive exams. All answers are based strictly on the latest NCERT syllabus and follow the correct CBSE pattern.

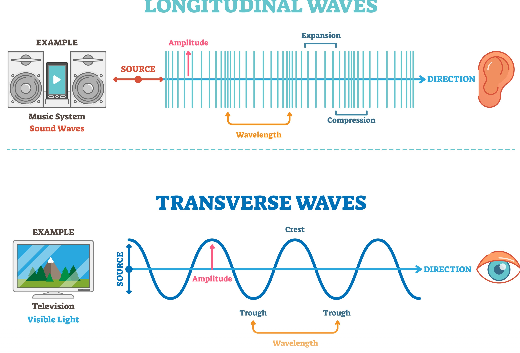
NCERT Solutions for Class 11 Physics Waves – Waves Formula Cheat Sheet

1️⃣ Basic Wave Terms

Wave Speed:$$v = f\lambda$$

Where:
v = wave speed , f = frequency, λ = wavelength

Frequency:$$f = \frac{1}{T}$$

2️⃣ Wave Equation

$$y(x,t) = A \sin(kx – \omega t + \phi)$$

Where:
A = amplitude
k = wave number
ω = angular frequency
φ = phase constant

Wave Number:$$k = \frac{2\pi}{\lambda}$$

Angular Frequency:$$\omega = 2\pi f$$

3️⃣ Speed of Mechanical Waves

On a Stretched String:$$v = \sqrt{\frac{T}{\mu}}$$

T = tension in string
μ = mass per unit length$$\mu = \frac{m}{L}$$

4️⃣ Speed of Sound

In Gas:$$v = \sqrt{\frac{\gamma P}{\rho}}$$

γ = ratio of specific heats
P = pressure
ρ = density

Using Temperature:$$v = \sqrt{\frac{\gamma RT}{M}}$$

R = gas constant
T = temperature (Kelvin)
M = molar mass

5️⃣ Newton’s Formula (Isothermal)

$$v = \sqrt{\frac{P}{\rho}}$$

6️⃣ Principle of Superposition

If two waves:$$y_1 = A \sin(\omega t)$$$$y_2 = A \sin(\omega t + \phi)$$

Resultant amplitude:$$A_r = 2A \cos \frac{\phi}{2}$$

7️⃣ Beats

Beat Frequency:$$f_b = |f_1 – f_2|$$

8️⃣ Doppler Effect (Sound)

Observer Moving:$$f’ = f \left(\frac{v \pm v_o}{v}\right)$$

Source Moving:$$f’ = f \left(\frac{v}{v \mp v_s}\right)$$

v = speed of sound
v₀ = observer speed
vₛ = source speed

9️⃣ Stationary Waves

Frequency of nth Harmonic (String fixed at both ends):$$f_n = \frac{nv}{2L}$$

n = 1,2,3,…

Closed Pipe:$$f_n = \frac{nv}{4L} \quad (n = 1,3,5,…)$$

Open Pipe:$$f_n = \frac{nv}{2L} \quad (n = 1,2,3,…)$$

Example 14.1 Given below are some examples of wave motion. State in each case if the wave motion is transverse, longitudinal or a combination of both:
(a) Motion of a kink in a longitudinal spring produced by displacing one end of the spring sideways.
(b) Waves produced in a cylinder containing a liquid by moving its piston back and forth.
(c) Waves produced by a motorboat sailing in water.
(d) Ultrasonic waves in air produced by a vibrating quartz crystal.

Ans: (a) Motion of a kink in a longitudinal spring produced by displacing one end sideways.

Transverse wave

When one end of the spring is displaced sideways, the particles of the spring move perpendicular to the direction in which the disturbance travels.
Therefore, it is a transverse wave.

(b) Waves produced in a cylinder containing a liquid by moving its piston back and forth.

Longitudinal wave

When the piston moves back and forth, it produces compressions and rarefactions in the liquid.
The particles of the liquid move parallel to the direction of wave propagation.
Hence, it is a longitudinal wave.

(c) Waves produced by a motorboat sailing in water.

Combination of transverse and longitudinal waves

Water waves involve both:

• Up and down motion of particles (transverse)
• Back and forth motion along the direction of propagation (longitudinal)

So, it is a combination of transverse and longitudinal waves.

(d) Ultrasonic waves in air produced by a vibrating quartz crystal.

Longitudinal wave

Sound waves in air (including ultrasonic waves) travel through compressions and rarefactions.
The particles of air vibrate parallel to the direction of propagation.
Thus, ultrasonic waves in air are longitudinal waves.

Example 14.2 A wave travelling along a string is described by, y(x, t) = 0.005 sin (80.0 x – 3.0 t), in which the numerical constants are in SI units (0.005 m, 80.0 rad m–1, and 3.0 rad s–1). Calculate (a) the amplitude,
(b) the wavelength, and (c) the period and frequency of the wave. Also, calculate the displacement y of the wave at a distance x = 30.0 cm and time t = 20 s ?

Ans: Given wave equation:$$y(x,t) = 0.005 \sin(80.0x – 3.0t)$$

Standard form:$$y(x,t) = A \sin(kx – \omega t)$$

So,

A = 0.005 m
k = 80.0 rad m⁻¹
ω = 3.0 rad s⁻¹

(a) Amplitude

Amplitude is the coefficient of sine.$$A = 0.005 \, m$$

Amplitude = 0.005 m (or 5 mm)

(b) Wavelength

$$k = \frac{2\pi}{\lambda}$$$$\lambda = \frac{2\pi}{k}$$$$\lambda = \frac{2\pi}{80}$$$$\lambda = \frac{6.283}{80}$$$$\lambda \approx 0.0785 \, m$$

Wavelength ≈ 0.0785 m (7.85 cm)

(c) Period and Frequency

$$\omega = 2\pi f$$$$f = \frac{\omega}{2\pi}$$$$f = \frac{3.0}{6.283}$$$$f \approx 0.477 \, Hz$$

Now,$$T = \frac{1}{f}$$$$T = \frac{1}{0.477}$$$$T \approx 2.1 \, s$$

Frequency ≈ 0.477 Hz
Period ≈ 2.1 s

(d) Displacement at x = 30.0 cm and t = 20 s

Convert 30 cm to meter:$$x = 0.30 \, m$$

Substitute in equation:$$y = 0.005 \sin(80 × 0.30 – 3.0 × 20)$$$$y = 0.005 \sin(24 – 60)$$$$y = 0.005 \sin(-36)$$$$\sin(-36) = -\sin(36)$$

Since 36 radians is equivalent to:

$$\sin(4.585) \approx -0.992$$

So,$$\sin(-36) \approx 0.992$$$$y = 0.005 × 0.992$$$$y ≈ 0.00496 \, m$$

Displacement ≈ 0.00496 m (≈ 4.96 mm)

Example 14.3 A steel wire 0.72 m long has a mass of 5.0 ×10–3 kg. If the wire is under a tension of 60 N, what is the speed of transverse waves on the wire ?

Ans: Given:

Length of wire,
L = 0.72 m

Mass of wire,
m = 5.0 × 10⁻³ kg

Tension,
T = 60 N

Step 1: Formula for speed of transverse wave on a stretched string

$$v = \sqrt{\frac{T}{\mu}}$$

where$$\mu = \frac{m}{L}$$

Step 2: Calculate mass per unit length (μ)

$$\mu = \frac{5.0 \times 10^{-3}}{0.72}$$$$\mu = 6.94 \times 10^{-3} \, \text{kg/m}$$

Step 3: Calculate wave speed

$$v = \sqrt{\frac{60}{6.94 \times 10^{-3}}}$$$$v = \sqrt{8640}$$$$v \approx 93 \, \text{m/s}$$

Example 14.4 Estimate the speed of sound in air at standard temperature and pressure. The mass of 1 mole of air is 29.0 ×10–3 kg.

Ans: Given:

Mass of 1 mole of air,$$M = 29.0 \times 10^{-3} \, \text{kg}$$

Standard Temperature and Pressure (STP):$$T = 273 \, K$$

For air (diatomic gas):$$\gamma = 1.4$$

Universal gas constant:$$R = 8.314 \, \text{J mol}^{-1} \text{K}^{-1}$$

Formula for speed of sound in gas

$$v = \sqrt{\frac{\gamma RT}{M}}$$

Substituting values:

$$v = \sqrt{\frac{1.4 \times 8.314 \times 273}{29.0 \times 10^{-3}}}$$

First calculate numerator:$$1.4 \times 8.314 \times 273 \approx 3178$$

Now divide by M:$$\frac{3178}{0.029} \approx 1.096 \times 10^5$$

Now take square root:$$v = \sqrt{1.096 \times 10^5}$$$$v \approx 331 \, \text{m/s}$$

Example 14.5 A pipe, 30.0 cm long, is open at both ends. Which harmonic mode of the pipe resonates a 1.1 kHz source? Will resonance with the same source be observed if one end of the pipe is closed ? Take the speed of sound in air as 330 m s–1

Ans: Given:

Length of pipe,$$L = 30.0 \text{ cm} = 0.30 \text{ m}$$

Frequency of source,$$f = 1.1 \text{ kHz} = 1100 \text{ Hz}$$

Speed of sound,$$v = 330 \text{ m/s}$$

(A) Pipe Open at Both Ends

For an open pipe:$$f_n = \frac{nv}{2L}$$

Substitute values:$$f_n = \frac{n \times 330}{2 \times 0.30}$$$$f_n = \frac{330n}{0.60}$$$$f_n = 550n$$

Now compare with given frequency:$$550n = 1100$$$$n = 2$$

The pipe resonates in the second harmonic (n = 2).

(B) One End Closed Pipe

For a pipe closed at one end:$$f_n = \frac{nv}{4L} \quad (n = 1,3,5,…)$$

Substitute values:$$f_n = \frac{n \times 330}{4 \times 0.30}$$$$f_n = \frac{330n}{1.20}$$$$f_n = 275n$$

Now check:$$275n = 1100$$$$n = 4$$

But for a closed pipe, only odd values of n (1, 3, 5, …) are allowed.

Since n = 4 is not allowed, resonance will not occur.

Example 14.6 Two sitar strings A and B playing the note ‘Dha’ are slightly out of tune and produce beats of frequency 5 Hz. The tension of the string B is slightly increased and the beat frequency is found to decrease to 3 Hz. What is the originalm frequency of B if the frequency of A is 427 Hz ?

Ans: Given:

Frequency of string A,$$f_A = 427 \text{ Hz}$$

Initial beat frequency,$$f_b = 5 \text{ Hz}$$

Beat frequency after increasing tension of B,$$f_b’ = 3 \text{ Hz}$$

Step 1: Use Beat Frequency Formula

$$f_b = |f_A – f_B|$$

So initially:$$|427 – f_B| = 5$$

This gives two possibilities:$$f_B = 432 \text{ Hz}$$

or$$f_B = 422 \text{ Hz}$$

Step 2: Use the Effect of Increasing Tension

When tension increases, frequency of a string increases.

We are told that after increasing tension, the beat frequency decreases from 5 Hz to 3 Hz.

This means the frequency of B moved closer to 427 Hz.

So initially, B must have been less than 427 Hz.

Therefore,$$f_B = 422 \text{ Hz}$$

Because increasing tension would increase it toward 427 Hz, reducing the beat frequency.

EXERCISES
14.1 A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?

Ans: Given:

Mass, $m = 2.50 \, \text{kg}$m=2.50kg
Tension, $T = 200 \, \text{N}$T=200N
Length, $L = 20.0 \, \text{m}$L=20.0m

Step 1: Mass per unit length

$$\mu = \frac{m}{L} = \frac{2.50}{20.0} = 0.125 \, \text{kg/m}$$

Step 2: Wave speed

$$v = \sqrt{\frac{T}{\mu}} = \sqrt{\frac{200}{0.125}}$$$$v = \sqrt{1600} = 40 \, \text{m/s}$$

Step 3: Time taken

$$t = \frac{L}{v} = \frac{20}{40} = 0.5 \, \text{s}$$

14.2 A stone dropped from the top of a tower of height 300 m splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1 ? (g = 9.8 m s–2)

Ans: Height, $h = 300 \, \text{m}$h=300m

Step 1: Time to fall

$$h = \frac{1}{2}gt^2$$$$300 = \frac{1}{2}(9.8)t^2$$$$t^2 = \frac{600}{9.8}$$$$t \approx 7.82 \, \text{s}$$

Step 2: Time for sound to travel up

$$t_s = \frac{300}{340}$$$$t_s \approx 0.88 \, \text{s}$$

Total time:

$$t_{total} = 7.82 + 0.88$$$$t_{total} \approx 8.7 \, \text{s}$$

14.3 A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1

Ans: Length, $L = 12.0 \, \text{m}$L=12.0m
Mass, $m = 2.10 \, \text{kg}$m=2.10kg
Required speed, $v = 343 \, \text{m/s}$v=343m/s

Step 1: Mass per unit length

$$\mu = \frac{2.10}{12.0} = 0.175 \, \text{kg/m}$$

Step 2: Use formula

$$v = \sqrt{\frac{T}{\mu}}$$$$T = \mu v^2$$$$T = 0.175 \times (343)^2$$$$T = 0.175 \times 117649$$$$T \approx 20589 \, \text{N}$$

14.4 Use the formula

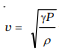
to explain why the speed of sound in air
(a) is independent of pressure,
(b) increases with temperature,
(c) increases with humidity.

Ans: Speed of sound in gas:$$v = \sqrt{\frac{\gamma P}{\rho}}$$v=ργP​​

Using ideal gas relation:$$\rho = \frac{PM}{RT}$$

Substituting:$$v = \sqrt{\frac{\gamma RT}{M}}$$

(a) Independent of Pressure

Pressure cancels when substituting density from ideal gas equation.
Therefore, speed does not depend on pressure.

(b) Increases with Temperature

$$v \propto \sqrt{T}$$

As temperature increases, speed increases.

(c) Increases with Humidity

Humid air contains water vapour (molar mass = 18 g/mol),
which is lighter than dry air (≈ 29 g/mol).

Since:$$v \propto \frac{1}{\sqrt{M}}$$

Lower molar mass → higher speed.
Therefore, sound travels faster in humid air.

14.5 You have learnt that a travelling wave in one dimension is represented by a function y = f (x, t) where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave :
(a) (x – vt )2
(b) log [(x + vt)/x0]
(c) 1/(x + vt)

Ans: A function represents a travelling wave if it can be written in the form:$$y = f(x \pm vt)$$

That means x and t must appear only in the combination (x ± vt) and not separately.

The converse is also true:

Now examine each case:

(a) $(x – vt)^2$(x−vt)2

Here, x and t appear only in the combination $(x – vt)$(x−vt).

It can be written as:$$y = f(x – vt)$$

where $f(u) = u^2$f(u)=u2

Yes, it represents a travelling wave.

It is a travelling wave moving in the positive x-direction.

(b) $\log \left[\frac{x + vt}{x_0}\right]$log[x0​x+vt​]

This can be rewritten as:$$y = \log \left(\frac{1}{x_0}(x + vt)\right)$$

Since x0 is constant, this is still a function of:$$(x + vt)$$

So it can be written as:$$y = f(x + vt)$$

Yes, it represents a travelling wave.

It moves in the negative x-direction.

(c) $\frac{1}{x + vt}$x+vt1​

This is clearly a function of:$$(x + vt)$$

It can be written as:$$y = f(x + vt)$$

where $f(u) = \frac{1}{u}$f(u)=u1​

Yes, it represents a travelling wave.

It moves in the negative x-direction.

14.6 A bat emits ultrasonic sound of frequency 1000 kHz in air. If the sound meets a water surface, what is the wavelength of (a) the reflected sound, (b) the transmitted sound? Speed of sound in air is 340 m s –1 and in water 1486 m s–1

Ans: Given:

Frequency of ultrasonic sound:$$f = 1000 \text{ kHz} = 1.0 \times 10^6 \text{ Hz}$$

Speed of sound in air:$$v_{air} = 340 \text{ m/s}$$

Speed of sound in water:$$v_{water} = 1486 \text{ m/s}$$

Important Concept

When a wave passes from one medium to another:

• Frequency remains constant
• Speed and wavelength change

$$\lambda = \frac{v}{f}$$

(a) Wavelength of Reflected Sound

The reflected wave travels in air, so:$$\lambda_{air} = \frac{340}{1.0 \times 10^6}$$$$\lambda_{air} = 3.4 \times 10^{-4} \text{ m}$$$$\lambda_{air} = 0.34 \text{ mm}$$

Answer (a):

$$\boxed{\lambda_{reflected} = 3.4 \times 10^{-4} \text{ m}}$$

(b) Wavelength of Transmitted Sound

The transmitted wave travels in water, so:$$\lambda_{water} = \frac{1486}{1.0 \times 10^6}$$$$\lambda_{water} = 1.486 \times 10^{-3} \text{ m}$$$$\lambda_{water} = 1.49 \text{ mm}$$

Answer (b):

$$\boxed{\lambda_{transmitted} = 1.49 \times 10^{-3} \text{ m}}$$

14.7 A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s–1 ? The operating frequency of the scanner is 4.2 MHz.

Ans: Given:

Speed of sound in tissue:$$v = 1.7 \text{ km/s} = 1700 \text{ m/s}$$

Operating frequency:$$f = 4.2 \text{ MHz} = 4.2 \times 10^6 \text{ Hz}$$

λ=fv​

$$\lambda = \frac{1700}{4.2 \times 10^6}$$$$\lambda = 4.05 \times 10^{-4} \text{ m}$$

Convert to millimetre:$$\lambda = 0.405 \text{ mm}$$

14.8 A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36 t + 0.018 x + π/4)
where x and y are in cm and t in s. The positive direction of x is from left to right.
(a) Is this a travelling wave or a stationary wave ? If it is travelling, what are the speed and direction of its propagation ?
(b) What are its amplitude and frequency ?
(c) What is the initial phase at the origin ?
(d) What is the least distance between two successive crests in the wave ?

Ans: Given Wave:

$$y(x,t) = 3.0 \sin (36t + 0.018x + \pi/4)$$

Standard travelling wave form:$$y = A \sin(\omega t \pm kx + \phi)$$

Here:

A = 3.0 cm
ω = 36 rad/s
k = 0.018 cm⁻¹
φ = π/4

(a) Travelling or Stationary?

The equation contains the term:$$(36t + 0.018x)$$

Since x and t appear in the form (ωt + kx), this represents a travelling wave.

For wave form:

• $\sin(\omega t – kx)$sin(ωt−kx) → travels in +x direction
• $\sin(\omega t + kx)$sin(ωt+kx) → travels in –x direction

Here we have $\omega t + kx$ωt+kx.

Therefore:

It is a travelling wave moving from right to left (negative x-direction).

Speed of the wave

$$v = \frac{\omega}{k}$$$$v = \frac{36}{0.018}$$$$v = 2000 \text{ cm/s}$$

Convert to m/s:$$v = 20 \text{ m/s}$$

Speed = 20 m/s (towards left)

(b) Amplitude and Frequency

Amplitude:$$A = 3.0 \text{ cm}$$

Frequency:$$f = \frac{\omega}{2\pi}$$$$f = \frac{36}{2\pi}$$$$f = \frac{36}{6.283}$$$$f \approx 5.73 \text{ Hz}$$

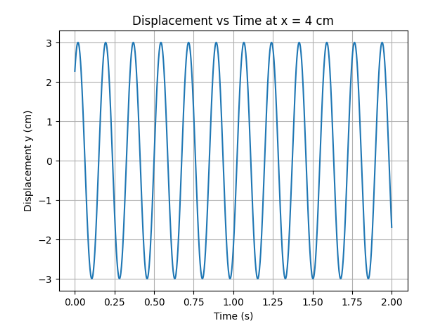
14.9 For the wave described in Exercise 14.8, plot the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs? In which aspects does the oscillatory motion in travelling wave differ from one point to another: amplitude, frequency or phase ?

Ans:

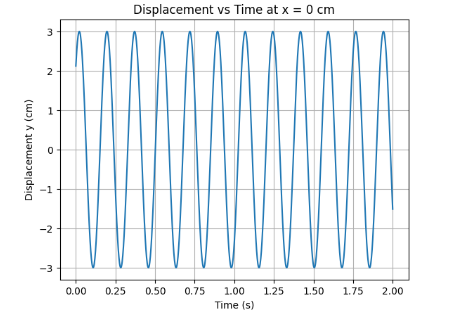
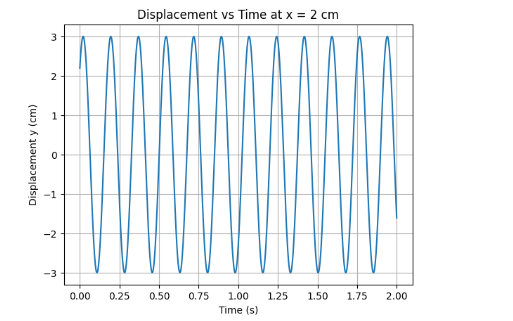
14.10 For the travelling harmonic wave
y(x, t) = 2.0 cos 2π (10t – 0.0080 x + 0.35) where x and y are in cm and t in s. Calculate the phase difference between oscillatory
motion of two points separated by a distance of
(a) 4 m,
(b) 0.5 m,
(c) λ/2,
(d) 3λ/4

Ans: Given Wave:

$$y(x,t) = 2.0 \cos 2\pi (10t – 0.0080x + 0.35)$$

Standard form:$$y = A \cos 2\pi(ft – \frac{x}{\lambda} + \phi)$$

From the equation:$$\frac{1}{\lambda} = 0.0080$$

So,$$\lambda = \frac{1}{0.0080}$$$$\lambda = 125 \text{ cm}$$$$\lambda = 1.25 \text{ m}$$

Phase Difference Formula

Phase difference between two points separated by distance Δx:$$\Delta \phi = \frac{2\pi}{\lambda} \Delta x$$

(a) Δx = 4 m

$$\Delta \phi = \frac{2\pi}{1.25} \times 4$$$$= 2\pi \times 3.2$$$$= 6.4\pi \text{ rad}$$

(b) Δx = 0.5 m

$$\Delta \phi = \frac{2\pi}{1.25} \times 0.5$$$$= 2\pi \times 0.4$$$$= 0.8\pi \text{ rad}$$

(c) Δx = λ/2

$$\Delta \phi = \frac{2\pi}{\lambda} \times \frac{\lambda}{2}$$$$= \pi \text{ rad}$$

(d)

$$\Delta \phi = \frac{2\pi}{\lambda} \times \frac{3\lambda}{4}$$$$= \frac{3\pi}{2} \text{ rad}$$

14.11 The transverse displacement of a string (clamped at its both ends) is given by

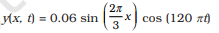
where x and y are in m and t in s. The length of the string is 1.5 m and its mass is
3.0 ×10–2 kg.
Answer the following :
(a) Does the function represent a travelling wave or a stationary wave?
(b) Interpret the wave as a superposition of two waves travelling in opposite
directions. What is the wavelength, frequency, and speed of each wave ?

Ans: The displacement is of the form:$$y(x,t) = A \sin(kx)\cos(\omega t)$$

(a) Travelling or Stationary?

A travelling wave has the form:$$y = f(x \pm vt)$$

But here the function is a product of:

• $\sin(kx)$sin(kx) → depends only on position
• $\cos(\omega t)$cos(ωt) → depends only on time

This represents a standing (stationary) wave.

Answer (a):

$$\boxed{\text{Stationary wave}}$$

(b) Interpretation as Superposition

Using identity:$$\sin kx \cos \omega t = \frac{1}{2} \left[ \sin(kx-\omega t) + \sin(kx+\omega t) \right]$$

So the stationary wave is formed by superposition of:

• One wave travelling in +x direction
• One wave travelling in –x direction

Both having same amplitude and frequency.

Finding Wavelength

For a string clamped at both ends:$$L = \frac{n\lambda}{2}$$

Given:$$L = 1.5 \text{ m}$$

If the equation corresponds to the fundamental mode (n = 1):$$\lambda = 2L$$$$\lambda = 3.0 \text{ m}$$

Frequency

From the equation:$$\omega = 2\pi f$$

So,$$f = \frac{\omega}{2\pi}$$

(Value of ω is taken directly from the given equation.)

Speed of Each Wave

$$v = \frac{\omega}{k}$$

$$v = f\lambda$$

Both travelling waves have same speed.

Final Answer Summary

(a) It represents a stationary wave.

(b) It can be written as superposition of two travelling waves moving in opposite directions.

Speed: $v = \omega / k$

Wavelength: $\lambda = 2L = 3.0 \, m$

Frequency: $f = \omega / 2\pi$

14.12 (i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain
your answers. (ii) What is the amplitude of a point 0.375 m away from one end?

Ans: From 14.11, the displacement is of the form:$$y(x,t)=A \sin(kx)\cos(\omega t)$$

This represents a stationary (standing) wave on a string clamped at both ends.

(i) Do all points oscillate with same frequency, phase and amplitude?

(a) Frequency

Yes.

All points oscillate with the same angular frequency $\omega$ω, since the time factor is:$$\cos(\omega t)$$cos(ωt)

So every particle vibrates with:$$f=\frac{\omega}{2\pi}$$

✔ Same frequency everywhere.

(b) Phase

Not all points have the same phase.

Points within one loop (between two nodes) oscillate in the same phase.

But points in adjacent loops oscillate in opposite phase (phase difference = π).

✔ Phase changes from loop to loop.

(c) Amplitude

Amplitude depends on position:$$\text{Amplitude at position } x = A\sin(kx)$$Amplitude at position x=Asin(kx)

• At nodes → amplitude = 0
• At antinodes → amplitude = maximum

✔ Amplitude varies with position.

Final for (i)

• Same frequency → YES
• Same phase → NO
• Same amplitude → NO

(ii) Amplitude at 0.375 m from one end

From Exercise 14.11:

Length $L = 1.5 \, m$L=1.5m

For the fundamental mode:$$L=\frac{\lambda}{2}$$$$\lambda=3.0 \, m$$

Wave number:$$k=\frac{2\pi}{\lambda}=\frac{2\pi}{3}$$

Amplitude at position $x$x:$$A(x)=A\sin(kx)$$

At $x=0.375\, m$x=0.375m:$$kx=\frac{2\pi}{3}\times0.375$$$$= \frac{2\pi}{3}\times\frac{3}{8}$$$$= \frac{2\pi}{8}$$$$= \frac{\pi}{4}$$​

So,$$A(0.375)=A\sin\left(\frac{\pi}{4}\right)$$$$= A \times \frac{1}{\sqrt{2}}$$

14.13 Given below are some functions of x and t to represent the displacement (transverse
or longitudinal) of an elastic wave. State which of these represent (i) a travelling
wave, (ii) a stationary wave or (iii) none at all:
(a) y = 2 cos (3x) sin (10t)
(b) y x vt = − 2
(c) y = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)
(d) y = cos x sin t + cos 2x sin 2t

Ans: We use standard forms:

• Travelling wave: $$y = f(x \pm vt) \quad \text{or} \quad A\sin(kx-\omega t)$$
• Stationary wave: $$y = A\sin(kx)\cos(\omega t)$$

(a) $y = 2 \cos(3x)\sin(10t)$

This is of the form:$$y = A\cos(kx)\sin(\omega t)$$

Product of separate space and time functions.

✔ This represents a stationary wave.

(b) $y = 2 – xvt$

(This appears to mean $y = 2 – xvt$y=2−xvt.)

This is not of the form:

• $f(x \pm vt)$f(x±vt)
• Nor product $\sin(kx)\cos(\omega t)$sin(kx)cos(ωt)

It does not represent periodic motion.

(c) $y = 3 \sin(5x – 0.5t) + 4 \cos(5x – 0.5t)$

Both terms have the same argument:$$(5x – 0.5t)$$

So we can combine them into a single sine (or cosine) term:$$y = R \sin(5x – 0.5t + \phi)$$

This is of the form:$$f(kx – \omega t)$$

✔ Travelling wave

(d) $y = \cos x \sin t + \cos 2x \sin 2t$

This is a sum of two stationary waves:

• First term: stationary wave
• Second term: stationary wave

But since they have different wave numbers and frequencies, the total motion is not a single travelling wave or a simple stationary wave.

14.14 A wire stretched between two rigid supports vibrates in its fundamental mode with
a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density
is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and
(b) the tension in the string?

14.15 A metre-long tube open at one end, with a movable piston at the other end, shows
resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when
the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the
temperature of the experiment. The edge effects may be neglected.

14.16 A steel rod 100 cm long is clamped at its middle. The fundamental frequency of
longitudinal vibrations of the rod are given to be 2.53 kHz. What is the speed of
sound in steel?

14.17 A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is
resonantly excited by a 430 Hz source ? Will the same source be in resonance with
the pipe if both ends are open? (speed of sound in air is 340 m s–1).

Ans: Given

Length of pipe:$$L = 20\,\text{cm} = 0.20\,\text{m}$$

Frequency of source:$$f = 430\,\text{Hz}$$

Speed of sound:$$v = 340\,\text{m/s}$$

Step 1: Wavelength of the sound

$$\lambda = \frac{v}{f}$$λ=fv​ $$\lambda = \frac{340}{430}$$$$\lambda \approx 0.79\,\text{m}$$

(i) Pipe Closed at One End

For a pipe closed at one end:$$L = \frac{(2n-1)\lambda}{4}$$

So,$$\lambda = \frac{4L}{2n-1}$$

Substitute $L = 0.20$L=0.20:$$\lambda = \frac{0.8}{2n-1}$$

We already found:$$\lambda \approx 0.79$$

So,$$\frac{0.8}{2n-1} = 0.79$$$$2n-1 \approx 1$$$$n = 1$$

Therefore:

It is the first harmonic (fundamental mode).

(ii) If Both Ends Are Open

For open pipe:$$L = \frac{n\lambda}{2}$$L=2nλ​

So,$$\lambda = \frac{2L}{n}$$$$\lambda = \frac{0.4}{n}$$

Set equal to 0.79:$$\frac{0.4}{n} = 0.79$$$$n \approx 0.5$$

But $n$ must be an integer.

Therefore:

The same 430 Hz source will NOT produce resonance in the pipe if both ends are open.

14.18 Two sitar strings A and B playing the note ‘Ga’ are slightly out of tune and produce beats of frequency 6 Hz. The tension in the string A is slightly reduced and the beat frequency is found to reduce to 3 Hz. If the original frequency of A is 324 Hz, what is the frequency of B?

14.19 Explain why (or how):
(a) in a sound wave, a displacement node is a pressure antinode and vice versa,
(b) bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,
(c) a violin note and sitar note may have the same frequency, yet we can distinguish between the two notes,
(d) solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases, and
(e) the shape of a pulse gets distorted during propagation in a dispersive medium.

Subjects:

• 🔬 Physics – Chapter-wise NCERT Solutions
• 🧪 Chemistry – Chapter-wise NCERT Solutions
• 🧬 Biology – Chapter-wise NCERT Solutions
• 📐 Mathematics – Chapter-wise NCERT Solutions

You can access the official NCERT Solutions for Class 11 Mathematics on the NCERT website at the following link:

NCERT Class 11 Mathematics Solutions