Geometry is not just about shapes and measurements—it’s also about precision and technique. In Chapter 11: Constructions, we dive into the world of geometrical tools and learn how to create accurate figures using only a compass and a straightedge (ruler without measurement markings). This chapter strengthens your understanding of geometrical principles by applying them in practical constructions.
Class 9 Math Ch 11 Constructions Ex 11.1 to Ex 11.2 – Textbook
EX 11.1
Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Step of Construction:
Step I : Draw \overline { AB }.
Step II : Taking O as centre and having a suitable radius, draw a semicircle, which cuts \overline { OA } at B.
Step III : Keeping the radius same, divide the semicircle into three equal parts such that \breve { BC } =\quad \breve { CD } \quad =\quad \breve { DE } .
Step IV : Draw \overline { OC } and \overline { OD }.
Step V : Draw \overline { OF }, the bisector of ∠COD.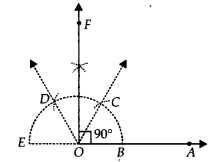
NCERT books
Thus, ∠AOF = 90°
Justification:
∵ O is the centre of the semicircle and it is divided into 3 equal parts.
∴ \breve { BC } =\quad \breve { CD } \quad =\quad \breve { DE }
⇒ ∠BOC = ∠COD = ∠DOE [Equal chords subtend equal angles at the centre]
And, ∠BOC + ∠COD + ∠DOE = 180°
⇒ ∠BOC + ∠BOC + ∠BOC = 180°
⇒ 3∠BOC = 180°
⇒ ∠BOC = 60°
Similarly, ∠COD = 60° and ∠DOE = 60°
∵ \overline { OF } is the bisector of ∠COD
∴ ∠COF = \frac { 1 }{ 2 } ∠COD = \frac { 1 }{ 2 } (60°) = 30°
Now, ∠BOC + ∠COF = 60° + 30°
⇒ ∠BOF = 90° or ∠AOF = 90°
Ex 11.1 Class 9 Maths Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
Steps of Construction:
Stept I : Draw \overline { OA }.
Step II : Taking O as centre and with a suitable radius, draw a semicircle such that it intersects \overline { OA }. at B.
Step III : Taking B as centre and keeping the same radius, cut the semicircle at C. Now, taking C as centre and keeping the same radius, cut the semicircle at D and similarly, cut at E, such that \breve { BC } =\quad \breve { CD } \quad =\quad \breve { DE }
Step IV : Draw \overline { OC } and \overline { OD }.
Step V : Draw \overline { OF }, the angle bisector of ∠BOC.
Step VI : Draw \overline { OG }, the ajngle bisector of ∠FOC.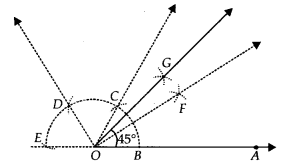
Thus, ∠BOG = 45° or ∠AOG = 45°
Justification:
∵ \breve { BC } =\quad \breve { CD } \quad =\quad \breve { DE }
∴ ∠BOC = ∠COD = ∠DOE [Equal chords subtend equal angles at the centre]
Since, ∠BOC + ∠COD + ∠DOE = 180°
⇒ ∠BOC = 60°
∵ \overline { OF } is the bisector of ∠BOC.
∴ ∠COF = \frac { 1 }{ 2 } ∠BOC = \frac { 1 }{ 2 }(60°) = 30° …(1)
Also, \overline { OG } is the bisector of ∠COF.
∠FOG = \frac { 1 }{ 2 }∠COF = \frac { 1 }{ 2 }(30°) = 15° …(2)
Adding (1) and (2), we get
∠COF + ∠FOG = 30° + 15° = 45°
⇒ ∠BOF + ∠FOG = 45° [∵ ∠COF = ∠BOF]
⇒ ∠BOG = 45°
Ex 11.1 Class 9 Maths Question 3.
Construct the angles of the following measurements
(i) 30°
(ii) 22 \frac { 1 }{ 2 } \circ
(iii) 15°
Solution:
(i) Angle of 30°
Steps of Construction:
Step I : Draw \overline { OA }.
Step II : With O as centre and having a suitable radius, draw an arc cutting \overline { OA } at B.
Step III : With centre at B and keeping the same radius as above, draw an arc to cut the previous arc at C.
Step IV : Join \overline { OC } which gives ∠BOC = 60°.
Step V : Draw \overline { OD }, bisector of ∠BOC, such that ∠BOD = \frac { 1 }{ 2 }∠BOC = \frac { 1 }{ 2 }(60°) = 30°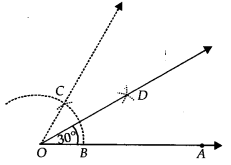
Thus, ∠BOD = 30° or ∠AOD = 30°
(ii) Angle of 22 \frac { 1 }{ 2 } \circ
Steps of Construction:
Step I : Draw \overline { OA }.
Step II : Construct ∠AOB = 90°
Step III : Draw \overline { OC }, the bisector of ∠AOB, such that
∠AOC = \frac { 1 }{ 2 }∠AOB = \frac { 1 }{ 2 }(90°) = 45°
Step IV : Now, draw OD, the bisector of ∠AOC, such that
∠AOD = \frac { 1 }{ 2 }∠AOC = \frac { 1 }{ 2 }(45°) = 22 \frac { 1 }{ 2 } \circ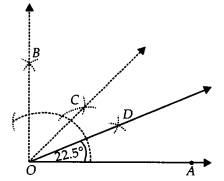
Thus, ∠AOD = 22 \frac { 1 }{ 2 } \circ
(iii) Angle of 15°
Steps of Construction:
Step I : Draw \overline { OA }.
Step II : Construct ∠AOB = 60°.
Step III : Draw OC, the bisector of ∠AOB, such that
∠AOC = \frac { 1 }{ 2 }∠AOB = \frac { 1 }{ 2 }(60°) = 30°
i.e., ∠AOC = 30°
Step IV : Draw OD, the bisector of ∠AOC such that
∠AOD = \frac { 1 }{ 2 }∠AOC = \frac { 1 }{ 2 }(30°) = 15°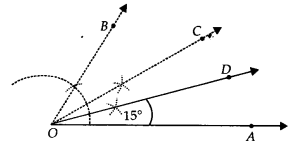
Thus, ∠AOD = 15°
Ex 11.1 Class 9 Maths Question 4.
Construct the following angles and verify by measuring them by a protractor
(i) 75°
(ii) 105°
(iii) 135°
Solution:
Step I : Draw \overline { OA }.
Step II : With O as centre and having a suitable radius, draw an arc which cuts \overline { OA } at B.
Step III : With centre B and keeping the same radius, mark a point C on the previous arc.
Step IV : With centre C and having the same radius, mark another point D on the arc of step II.
Step V : Join \overline { OC } and \overline { OD }, which gives ∠COD = 60° = ∠BOC.
Step VI : Draw \overline { OP }, the bisector of ∠COD, such that
∠COP = \frac { 1 }{ 2 }∠COD = \frac { 1 }{ 2 }(60°) = 30°.
Step VII: Draw \overline { OQ }, the bisector of ∠COP, such that
∠COQ = \frac { 1 }{ 2 }∠COP = \frac { 1 }{ 2 }(30°) = 15°.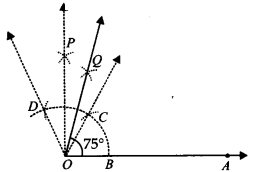
Thus, ∠BOQ = 60° + 15° = 75°∠AOQ = 75°
(ii) Steps of Construction:
Step I : Draw \overline { OA }.
Step II : With centre O and having a suitable radius, draw an arc which cuts \overline { OA } at B.
Step III : With centre B and keeping the same radius, mark a point C on the previous arc.
Step IV : With centre C and having the same radius, mark another point D on the arc drawn in step II.
Step V : Draw OP, the bisector of CD which cuts CD at E such that ∠BOP = 90°.
Step VI : Draw \overline { OQ }, the bisector of \breve { BC } such that ∠POQ = 15°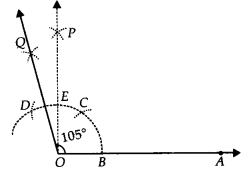
Thus, ∠AOQ = 90° + 15° = 105°
(iii) Steps of Construction:
Step I : Draw \overline { OP }.
Step II : With centre O and having a suitable radius, draw an arc which cuts \overline { OP } at A
Step III : Keeping the same radius and starting from A, mark points Q, R and S on the arc of step II such that \breve { AQ } =\quad \breve { QR } \quad =\quad \breve { RS } .
StepIV :Draw \overline { OL }, thebisector of \breve { RS } which cuts the arc \breve { RS } at T.
Step V : Draw \overline { OM }, the bisector of \breve { RT }.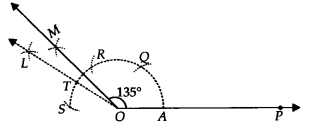
Thus, ∠POQ = 135°
Ex 11.1 Class 9 Maths Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Solution:
pt us construct an equilateral triangle, each of whose side = 3 cm(say).
Steps of Construction:
Step I : Draw \overline { OA }.
Step II : Taking O as centre and radius equal to 3 cm, draw an arc to cut \overline { OA } at B such that OB = 3 cm
Step III : Taking B as centre and radius equal to OB, draw an arc to intersect the previous arc at C.
Step IV : Join OC and BC.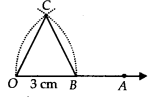
Thus, ∆OBC is the required equilateral triangle.
Justification:
∵ The arcs \breve { OC } and \breve { BC } are drawn with the same radius.
∴ \breve { OC } = \breve { BC }
⇒ OC = BC [Chords corresponding to equal arcs are equal]
∵ OC = OB = BC
∴ OBC is an equilateral triangle.
NCERT Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.2
Ex 11.2 Class 9 Maths Question 1.
Construct a ∆ ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Steps of Construction:
Step I : Draw \overline { BX }.
Step II : Along \overline { BX }, cut off a line segment BC = 7 cm.
Step III : At B, construct ∠CBY = 75°
Step IV : From \overline { BY }, cut off BD = 13 cm (= AB + AC)
Step V : Join DC.
Step VI : Draw a perpendicular bisector of CD which meets BD at A.
Step VII: Join AC.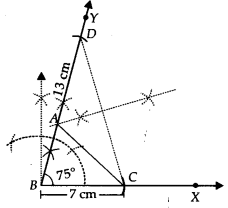
Thus, ∆ABC is the required triangle.
Ex 11.2 Class 9 Maths Question 2.
Construct a ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 35 cm.
Solution:
Steps of Construction:
Step I : Draw \overline { BX }.
Step II : Along \overline { BX }, cut off a line segment BC = 8 cm.
Step III : At B, construct ∠CBY = 45°
Step IV : From \overline { BX }, cut off BD = 3.5 cm (= AB – AC)
Step V : Join DC.
Step VI : Draw PQ, perpendicular bisector of DC, which intersects \overline { BY } at A.
Step VII: Join AC.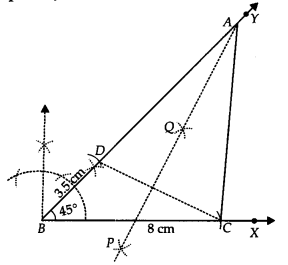
Thus, ∆ABC is the required triangle.
Ex 11.2 Class 9 Maths Question 3.
Construct a ∆ ABC in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.
Solution:
Steps of Construction:
Step I : Draw \overline { QX }.
Step II : Along \overline { QX }, cut off a line segment QR = 6 cm.
Step III : Construct a line YQY’ such that ∠RQY = 60°.
Step IV : Cut off QS = 2 cm (= PR – PQ) on QY’.
Step V : Join SR.
Step VI : Draw MN, perpendicular bisector of SR, which intersects QY at P.
Step VII: Join PR.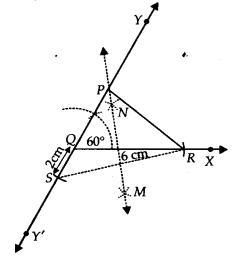
Thus, ∆PQR is the required triangle.
Ex 11.2 Class 9 Maths Question 4.
Construct a ∆ XYZ in which ∠Y = 30°, ∠Y = 90° and XY + YZ + ZX = 11 cm.
Solution:
Steps of Construction:
Step I : Draw a line segment AB = 11 cm = (XY+YZ + ZX)
Step II : Construct ∠BAP = 30°
Step III : Construct ∠ABQ = 90°
Step IV : Draw AR, the bisector of ∠BAP.
Step V : Draw BS, the bisector of ∠ABQ. Let AR and BS intersect at X.
Step VI : Draw perpendicular bisector of \overline { AX }, which intersects AB at Y.
Step VII: Draw perpendicular bisector of \overline { XB }, which intersects AB at Z.
Step VIII: Join XY and XZ.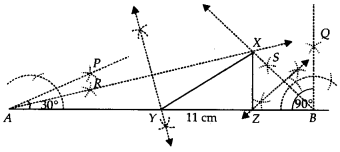
Thus, ∆XYZ is the required triangle.
Ex 11.2 Class 9 Maths Question 5.
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Solution:
Steps of Construction:
Step I : Draw BC = 12 cm.
Step II : At B, construct ∠CBY = 90°.
Step III : Along \overline { BY }, cut off a line segment BX = 18 cm.
Step IV : Join CX.
Step V : Draw PQ, perpendicular bisector of CX, which meets BX at A.
Step VI : Join AC.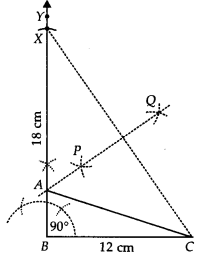
Thus, ∆ABC is the required triangle.
In this exercise Class 10 Maths Ch 7 Coordinate Geometry Ex 7.4, students learn how to find the area of a triangle using the coordinates of its vertices. The formula is easy to apply and helps in checking whether three given points are collinear. Below are the detailed, step-by-step solutions for all questions in Exercise 7.4, designed to help you understand the method clearly and prepare confidently for your exam.
Class 10 Maths Ch 7 Coordinate Geometry Ex 7.4-Text Book Answers
Ex 7.4 Class 10 Maths Question 1.
Determine the ratio, in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).
Solution:
Ex 7.4 Class 10 Maths Question 2.
Find a relation between x and y, if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution: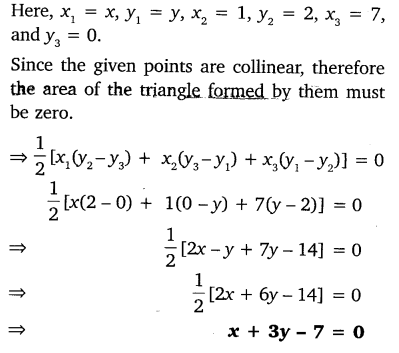
Ex 7.4 Class 10 Maths Question 3.
Find the centre of a circle passing through the points (6, -6), (3, -7) and (3, 3).
Solution:
Ex 7.4 Class 10 Maths Question 4.
The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.
Solution:

Ex 7.4 Class 10 Maths Question 5.
The class X students school in krishnagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of ∆PQR, if C is the origin?
Also, calculate the areas of the triangles in these cases. What do you observe?
Solution: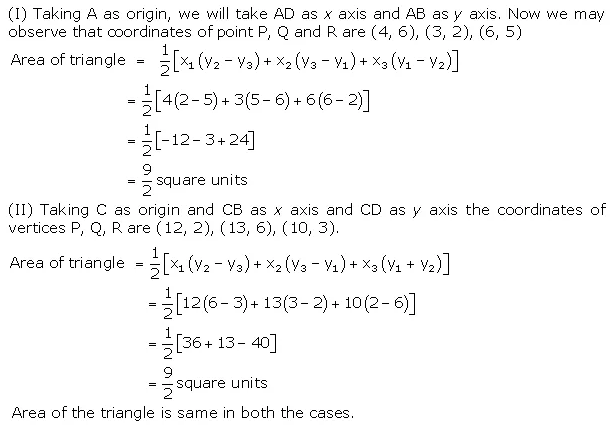
Ex 7.4 Class 10 Maths Question 6.
The vertices of a VABC are A(4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively. such that ADAB=AEAC=14. calculate the area of the ∆ADe and compare it with the area of ∆ABC.
Solution:

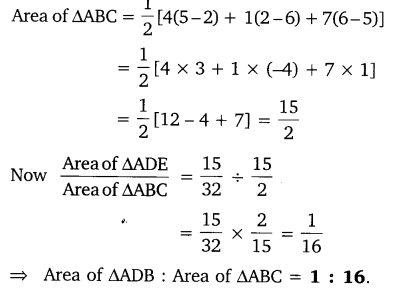
Ex 7.4 Class 10 Maths Question 7.
Let A(4, 2), B(6,5) and C(1, 4) be the vertices of ∆ABC.
(i) The median from A meters BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on the AD, such that AP: PD = 2: 1.
(iii) Find the coordinates of points Q and R on medians BE and CF respectively, such that BQ: QE = 2: 1 and CR: RF = 2: 1.
(iv) What do you observe?
[Note: The points which are common to all the three medians is called centroid and this point divides each median in the ratio 2: 1]
(v) If A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC, find the coordinates of the centroid of the triangles.
Solution: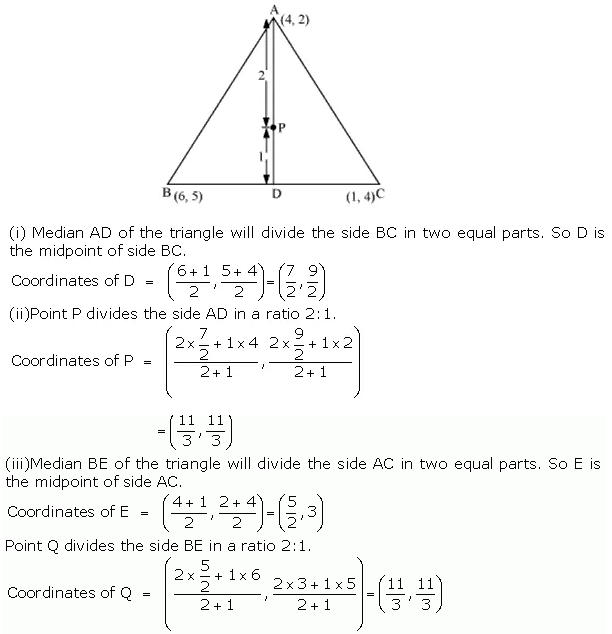


Ex 7.4 Class 10 Maths Question 8.
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1), P, Q, R and S are the mid-points of Ab, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Solution:

📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks :
