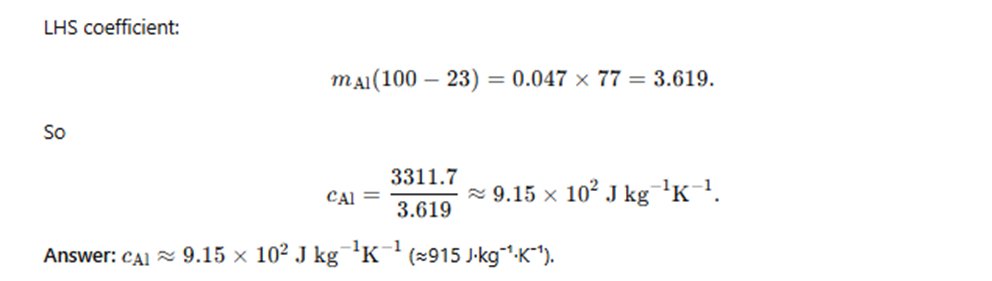Get complete Class 11 Physics notes for the chapter Thermal Properties of Matter Class 11 Notes with NCERT solutions, formula summary, derivations, solved numericals and important conceptual questions based on the CBSE syllabus.
NCERT In-text Questions – Thermal Properties of Matter Class 11 Notes
(From Thermal Properties of Matter)
Exercise 10.1
Q: The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively.
Express these temperatures on the Celsius and Fahrenheit scales.
Ans:
Step 1 — Convert Kelvin to Celsius
Formula:
Celsius temperature (°C) = K − 273.15
For Neon:
24.57 K − 273.15 = −248.58 °C
For Carbon dioxide:
216.55 K − 273.15 = −56.60 °C
Step 2 — Convert Celsius to Fahrenheit
Formula:
°F = (°C × 9/5) + 32
For Neon:
°F = (−248.58 × 9/5) + 32
= (−248.58 × 1.8) + 32
= −447.444 + 32
= −415.44 °F
For Carbon dioxide:
°F = (−56.60 × 1.8) + 32
= −101.88 + 32
= −69.88 °F
Exercise 10.2
Two absolute scales A and B have triple points of water defined to be 200 A and 350 B.
What is the relation between TA and TB ?
Ans: The triple point of water is the same physical temperature on both scales.
Therefore, temperatures on the two scales are proportional.
TA / TB = 200 / 350
200 divided by 350 simplifies to 4 divided by 7.
So the relation is:
TA = (4 / 7) TB
(or TB = (7 / 4) TA)
Exercise 10.3
The resistance of a thermometer varies with temperature according to the relation:
R = R₀ [ 1 + α (T − T₀) ]
where R₀ = 101.6 Ω at the triple point of water T₀ = 273.16 K.
The resistance of the thermometer is found to be 165.5 Ω at 600.5 K.
What is the temperature corresponding to a resistance of 123.4 Ω?
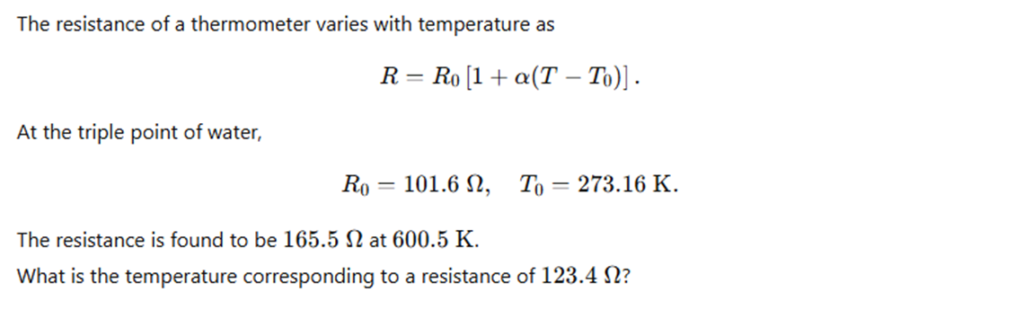
Exercise 10.4
Answer the following:
(a) Why is the triple point of water chosen as a standard fixed point?
(b) What is the other standard fixed point on the Kelvin scale?
(c) Why do we use 273.15 in the Celsius–Kelvin relation (T = 273.15 + t₍C₎) and not 273.16?
(d) What is the triple point on an absolute temperature scale whose unit of temperature is equal in size to the Fahrenheit degree?
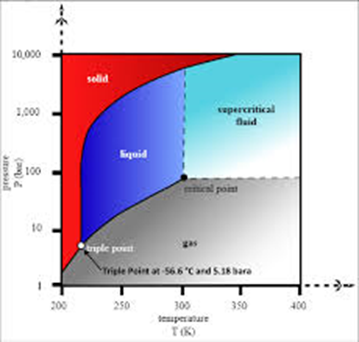
Phase diagram of water & CO₂
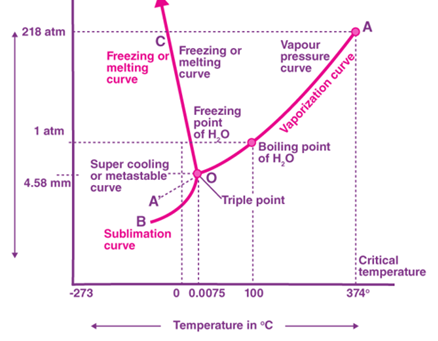
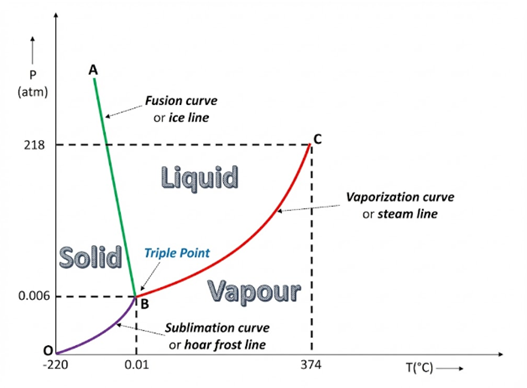
Answer: (a) The triple point of water is chosen as a standard fixed point because it is a unique and perfectly reproducible temperature at which ice, liquid water, and water vapour all coexist. Unlike the melting point or boiling point, it does not change with external pressure or impurities. Therefore, it provides a reliable reference for temperature scales.
(b) The other standard fixed point on the Kelvin scale is the boiling point of water at one atmosphere, which is approximately 373.16 kelvin.
(c) The Celsius–Kelvin conversion uses 273.15 instead of 273.16 because the Celsius scale was defined so that the melting point of ice is exactly zero degrees Celsius. The melting point is 0.01 kelvin below the triple point. To keep 0 degrees Celsius equal to 273.15 kelvin, we use 273.15 in the conversion formula. The triple point remains exactly 273.16 kelvin by definition.
(d) If an absolute temperature scale uses degrees the same size as Fahrenheit degrees, then the triple point of water (273.16 kelvin) becomes 491.69 on that scale. This is because one Fahrenheit degree is five-ninths of a kelvin, so the number of degrees is 273.16 multiplied by nine divided by five, which equals 491.69.
🔹 Exercise 10.5
Two ideal gas thermometers A and B use oxygen and hydrogen respectively. The following observations are made:
Temperature | Pressure in thermometer A | Pressure in thermometer B
Triple point of water | 1.250 × 10⁵ Pa | 0.200 × 10⁵ Pa
Normal melting point of sulphur | 1.797 × 10⁵ Pa | 0.287 × 10⁵ Pa
(a) What is the absolute temperature of the normal melting point of sulphur as read by thermometers A and B?
(b) What do you think is the reason behind the slight difference in the answers given by thermometers A and B (although the thermometers are not faulty)? What additional procedure is needed in the experiment to reduce the discrepancy between the two readings?

Exercise 10.6
In a constant–volume gas thermometer, the pressure at the triple point of water is 80 cm of mercury.
What is the pressure at the normal boiling point of water (100°C) if the thermometer reads 100°C at 100 cm of mercury?
What is the boiling point of water on the absolute scale?
Ans:

Exercise 10.7
A large steel wheel is to be fitted onto a shaft of the same material.
At 27°C, the outer diameter of the shaft is 8.70 cm and the diameter of the central hole in the wheel is 8.69 cm.
The shaft is cooled using dry ice.
At what temperature of the shaft will the wheel slip onto the shaft?
(Take the coefficient of linear expansion of steel as 1.20 × 10⁻⁵ K⁻¹.)

🔹 Exercise 10.8
A large steel wheel is to be fitted onto a shaft of the same material.
At 27°C, the outer diameter of the shaft is 8.70 cm and the diameter of the central hole in the wheel is 8.69 cm.
The shaft is cooled using dry ice.
At what temperature of the shaft will the wheel slip onto the shaft?
(Take the coefficient of linear expansion of steel = 1.20 × 10⁻⁵ K⁻¹.)
Ans:

Exercise 10.9
A brass wire 1.8 m long at 27°C is held taut with little tension between two rigid supports.
If the wire is cooled to a temperature of –39°C, what is the tension developed in the wire,
if its diameter is 2.0 mm?
Coefficient of linear expansion of brass = 2.0 × 10⁻⁵ K⁻¹
Young’s modulus of brass = 0.91 × 10¹¹ Pa

Exercise 10.10
A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter.
What is the change in length of the combined rod at 250°C, if the original lengths are at 40.0°C?
Is there a ‘thermal stress’ developed at the junction?
(The ends of the rod are free to expand.)
Coefficient of linear expansion of brass = 2.0 × 10⁻⁵ K⁻¹
Coefficient of linear expansion of steel = 1.2 × 10⁻⁵ K⁻¹
Exercise 10.11
The coefficient of volume expansion of glycerine is
49 × 10⁻⁵ per kelvin.
What is the fractional change in density for a temperature increase of 30 degrees Celsius?

Exercise 10.12
A 10 kW drilling machine drills a hole in a small aluminium block of mass 8.0 kg.
If 50 percent of the power used by the machine is converted into heat,
how much is the rise in temperature of the block in 2.5 minutes?
(Specific heat capacity of aluminium = 0.91 J g⁻¹ K⁻¹.

🔹 Exercise 10.13
A copper block of mass 2.5 kg is heated in a furnace to 500°C.
It is then placed on a large block of ice at 0°C.
What is the maximum amount of ice that can melt?
(Specific heat capacity of copper = 0.39 J g⁻¹ K⁻¹,
latent heat of fusion of ice = 3.35 × 10⁵ J kg⁻¹.)

Exercise 10.14
A metal block of mass 0.20 kg at 150°C is dropped into a copper calorimeter of water equivalent 0.025 kg
containing 150 cm³ of water at 27°C.
The final temperature of the mixture is 40°C.
Compute the specific heat capacity of the metal. (Specific heat capacity of water = 4.186 × 10³ J kg⁻¹ K⁻¹.)
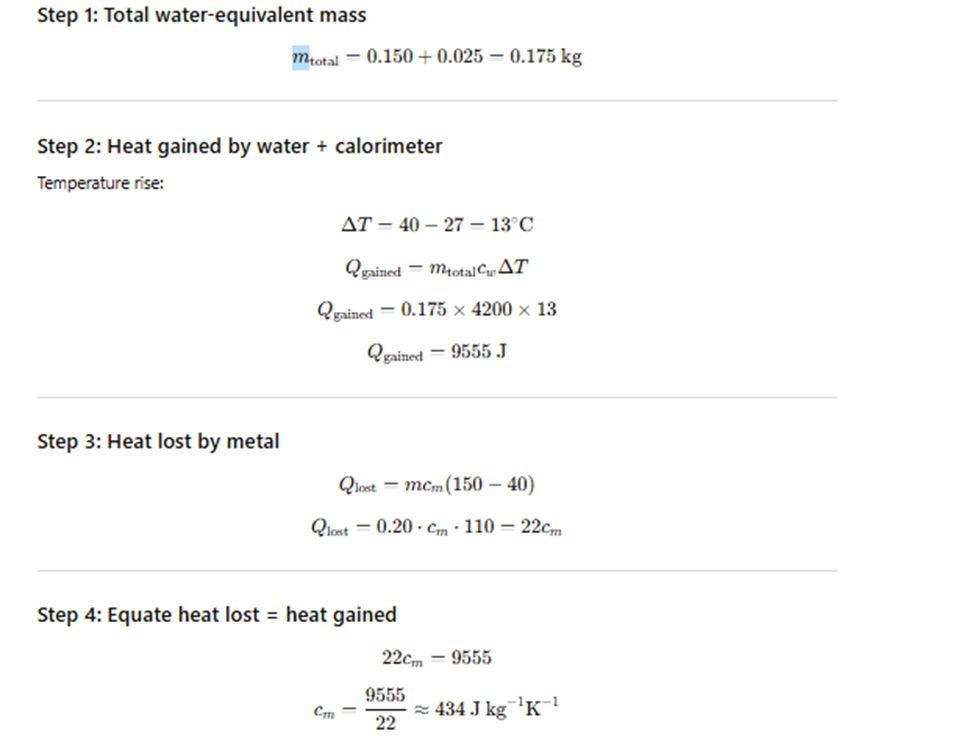
Exercise 10.15
The molar specific heat capacities of some gases at room temperature are given in the textbook table.
Explain why the values for real gases differ from the theoretical value for a monatomic ideal gas.
Why is the value for chlorine gas particularly high?



Exercise 10.16
A child of mass 30 kg is running a high fever of 101°F.
After taking medicine, the temperature falls to 98°F in 20 minutes.
Assuming the body behaves like water and loses heat only by sweating,
estimate the average rate of evaporation of sweat.
(Specific heat of water ≈ 4.186 × 10³ J kg⁻¹ K⁻¹,
latent heat of evaporation ≈ 580 cal g⁻¹.)


Exercise 10.17
A cubical icebox of side 30 cm has walls 5.0 cm thick.
The icebox contains 4.0 kg of ice at 0°C.
If the outside temperature is 45°C,
estimate how much ice will remain after 6 hours.
(Thermal conductivity of thermocole = 0.01 J s⁻¹ m⁻¹ K⁻¹,
latent heat of fusion of ice = 3.35 × 10⁵ J kg⁻¹.)
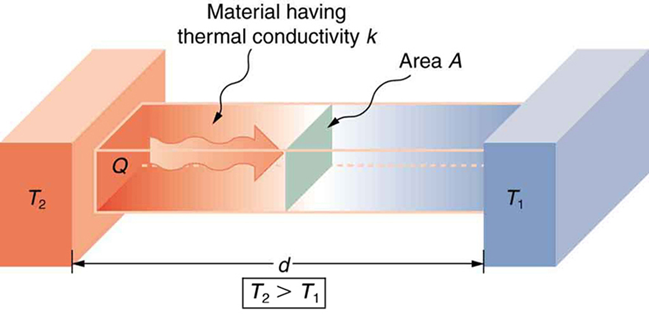


Exercise 10.18
At the base of a gas flame is a brass boiler with a circular base
of area 0.15 m² and thickness 1.0 cm.
The boiler contains water boiling at 6.0 kg per minute.
Estimate the temperature of the part of the flame in contact with the boiler.
(Thermal conductivity of brass = 109 J s⁻¹ m⁻¹ K⁻¹,
latent heat of vaporisation of water = 2.256 × 10⁶ J kg⁻¹.)

Exercise 10.19
Explain the following statements:
(a) Highly polished (shiny) surfaces are poor emitters of heat.
(b) A brass tumbler feels colder than a wooden tray on a cold morning.
(c) A red-hot iron rod in a furnace looks brighter than in the open air.
(d) The temperature of the earth would be extremely low if there were no atmosphere.
(e) Steam heating is preferred over hot-water heating in households.
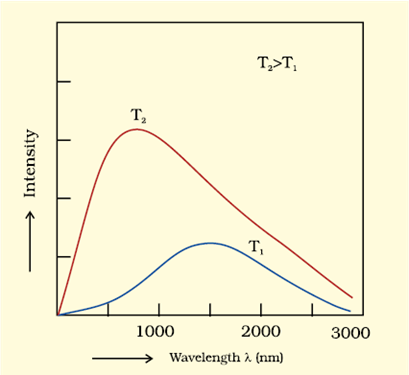
(a) Highly polished (shiny) surfaces are poor emitters of heat.
Polished surfaces reflect most of the incident radiation and absorb very little.
Since a good absorber is also a good emitter, a surface that absorbs poorly will also emit poorly.
Thus, shiny or polished surfaces radiate (emit) very little heat.
(b) A brass tumbler feels colder than a wooden tray on a cold morning.
Brass is a good conductor of heat, whereas wood is a poor conductor (insulator).
When you touch the brass tumbler, it rapidly conducts heat away from your hand, making your skin feel cold.
Wood does not draw away heat quickly, so it feels comparatively warmer.
(c) A red-hot iron rod in a furnace looks brighter than in the open air.
Inside the furnace, the surroundings are also very hot and emit thermal radiation.
Thus, the rod receives radiation from all sides and appears brighter.
In open air, the surroundings are cooler and do not emit radiation back, so the rod looks less bright even at the same temperature.
(d) The temperature of the earth would be extremely low if there were no atmosphere.
The atmosphere contains gases like water vapour and carbon dioxide that trap infrared radiation emitted by the earth’s surface (greenhouse effect).
If this trapping did not occur, most of the heat would escape into space, making the earth extremely cold — much below freezing temperatures.
(e) Steam heating is preferred over hot-water heating in households.
Steam at 100°C contains a very large amount of latent heat of vaporisation.
When steam condenses on surfaces inside heaters, it releases this large amount of heat, warming the room more effectively.
Thus, steam provides more heat energy than the same mass of hot water and heats rooms faster and more uniformly.
🔹 Exercise 10.20
A body cools from 80°C to 50°C in 5 minutes.
The surrounding temperature is 20°C.
How long will the body take to cool from 60°C to 30°C?
(Use Newton’s law of cooling.)

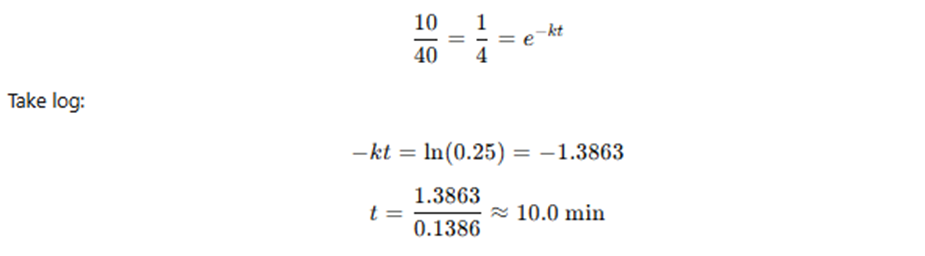
Examples with Diagrams (from the chapter)
Here are all Examples from your chapter along with diagrams:
Example 10.1 – Show that the coefficient of area expansion, (ΔA / A) / ΔT, of a rectangular sheet of a solid is twice its linear expansivity, αₗ.


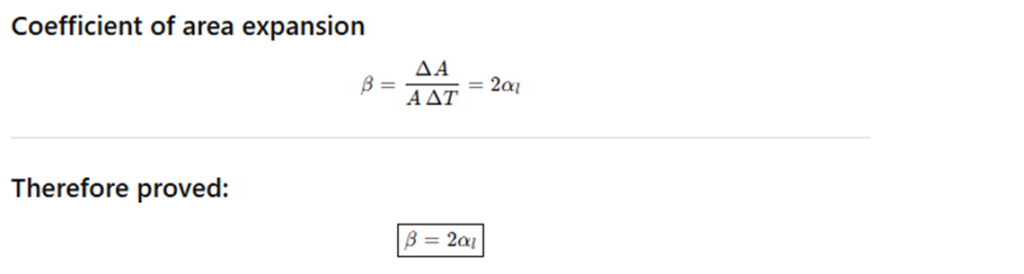
Example 10.2 – A blacksmith fixes an iron ring on the rim of the wooden wheel of a horse-cart. The diameter of the rim and the iron ring are 5.243 m and 5.231 m respectively at 27 °C. To what temperature should the ring be heated so as to fit the rim of the wheel? (Take coefficient of linear expansion of steel = 1.20 × 10⁻⁵ K⁻¹.)


Example 10.3 – A sphere of mass 0.047 kg of aluminium is placed for sufficient time in a vessel containing boiling water, so that the sphere is at 100 °C. It is then immediately transferred to a copper calorimeter of mass 0.14 kg containing 0.25 kg of water at 20 °C. The temperature of the water rises and attains a steady value of 23 °C. Calculate the specific heat capacity of aluminium.