Welcome to Trigonometry Exercise 8.1-Class 10 NCERT. In this exercise, you’ll learn how to find the values of trigonometric ratios such as sine, cosine, and tangent for specific angles. These ratios form the foundation of trigonometry and are essential for solving advanced problems in later exercises.
Exercise 8.1 introduces you to trigonometric values of standard angles like 0°, 30°, 45°, 60°, and 90°, using a right-angled triangle. These NCERT solutions provide step-by-step explanations to help you understand the concepts easily and build confidence in solving similar problems.
Whether you’re preparing for your board exams or revising the chapter, these solutions are perfect for strengthening your basics in trigonometry.
Question 1: In ΔABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
Solution:
Using the Pythagorean theorem, find AC:
AC² = AB² + BC² = 24² + 7² = 576 + 49 = 625
AC = √625 = 25 cm
Now, calculate the trigonometric ratios:
sin A = BC/AC = 7/25
cos A = AB/AC = 24/25
(ii) sin C, cos C
Since triangle ABC is right-angled at B, and angle C is the complement of angle A, we use the fact that:
sin C = cos A and cos C = sin A
So:
sin C = 24/25, cos C = 7/25
Question 2: In Fig. 8.13, find tan P – cot R.
(Please provide the diagram for a more detailed answer.)
Question 3: If sin A = 3/4, calculate cos A and tan A.
Solution:
Using the identity sin² A + cos² A = 1:
(3/4)² + cos² A = 1
9/16 + cos² A = 1
cos² A = 1 – 9/16 = 16/16 – 9/16 = 7/16
cos A = √7/4
Now, calculate tan A = sin A / cos A:
tan A = (3/4) / (√7/4) = 3/√7 = 3√7/7
Question 4: Given 15 cot A = 8, find sin A and sec A.
Solution:
We know that cot A = cos A / sin A, and cot A = 8/15.
Thus, tan A = 15/8.
Using the identity sin² A + cos² A = 1 and tan A = sin A / cos A, we solve for sin A and sec A:
sin A = 8/17, sec A = 17/8
Question 5: Given sec θ = 13/12, calculate all other trigonometric ratios.
Solution:
Given sec θ = 13/12, we know sec θ = 1 / cos θ.
Thus, cos θ = 12/13.
Now, using sin² θ + cos² θ = 1, we find:
sin² θ = 1 – (12/13)² = 1 – 144/169 = 25/169
sin θ = 5/13
Now, tan θ = sin θ / cos θ = 5/12, and cot θ = 1 / tan θ = 12/5.
So, the trigonometric ratios are:
sin θ = 5/13, cos θ = 12/13, tan θ = 5/12, cot θ = 12/5
Question 6: If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:
Since cos A = cos B and the cosine function is one-to-one in the interval (0°, 90°), we can conclude that A = B.
Thus, ∠A = ∠B.
Question 7: If cot θ = 7/8, evaluate:
(i) (1 + sin θ)(1 – sin θ) / (1 + cos θ)(1 – cos θ)
(ii) cot² θ
(For both questions, use the relationships between trigonometric ratios and simplify the expressions accordingly.)
Trigonometry Exercise 8.1-Class 10 NCERT Text Book
Ex 8.1 Class 10 Maths Question 10.
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
Ex 8.1 Class 10 Maths Question 11.
State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = [Math Processing Error] for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = [Math Processing Error] for some angle.
Solution:
Trigonometry Exercise 8.1-Class 10 NCERT-Concept
Trigonometry
Trigonometry is the study of relationships between the sides and angles of a right-angled triangle.
Trigonometric Ratios
Trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
Let ∆ABC be a triangle right angled at B. Then the trigonometric ratios of the angle A in right ∆ABC are defined as follows: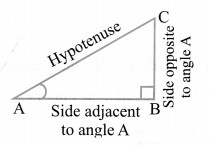

Note:
The values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle, if the angle remains same.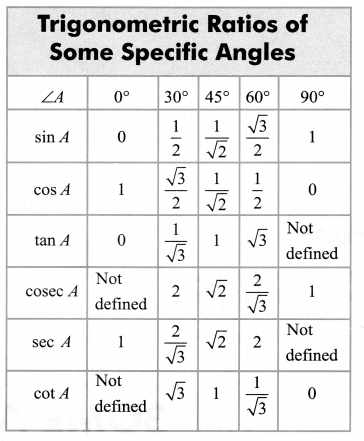
Trigonometric Ratios for Complementary Angles
sin (90° – A) = cos A
cos (90° – A) = sin A
tan (90° – A) = cot A
cot (90° – A) = tan A
sec (90° – A) = cosec A
cosec (90° – A) = sec A
Note:
Here (90° – A) is the complementary angle of A.
Trigonometric Identities
An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved.
(i) sin2θ + cos2θ = 1 [for 0° ≤ θ ≤ 90°]
(ii) sec2θ – tan2θ = 1 [for 0° ≤ θ ≤ 90°]
(iii) cosec2θ – cot2θ = 1 [for 0° < θ ≤ 90°]
Trigonometry Exercise 8.1–Class 10 NCERT -Explore All Classes
📘 Math & Science Solutions by Class
🔹 Class 10
🔹 Class 9
🔹 Class 8
🔹 Class 7
🔹 Class 6
🔹 Class 12
🔹 Class 11
- Class 11 Math Solutions
- Class 11 Physics Solutions
- Class 11 Chemistry Solutions
- Class 11 Biology Solutions
For the official Class 10 Mathematics Solutions, you can visit:
- NCERT Textbooks (for Class 10):
